题目

思路：

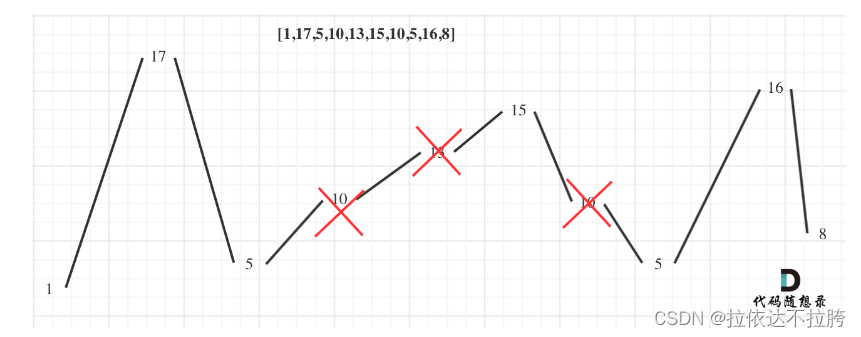
举例：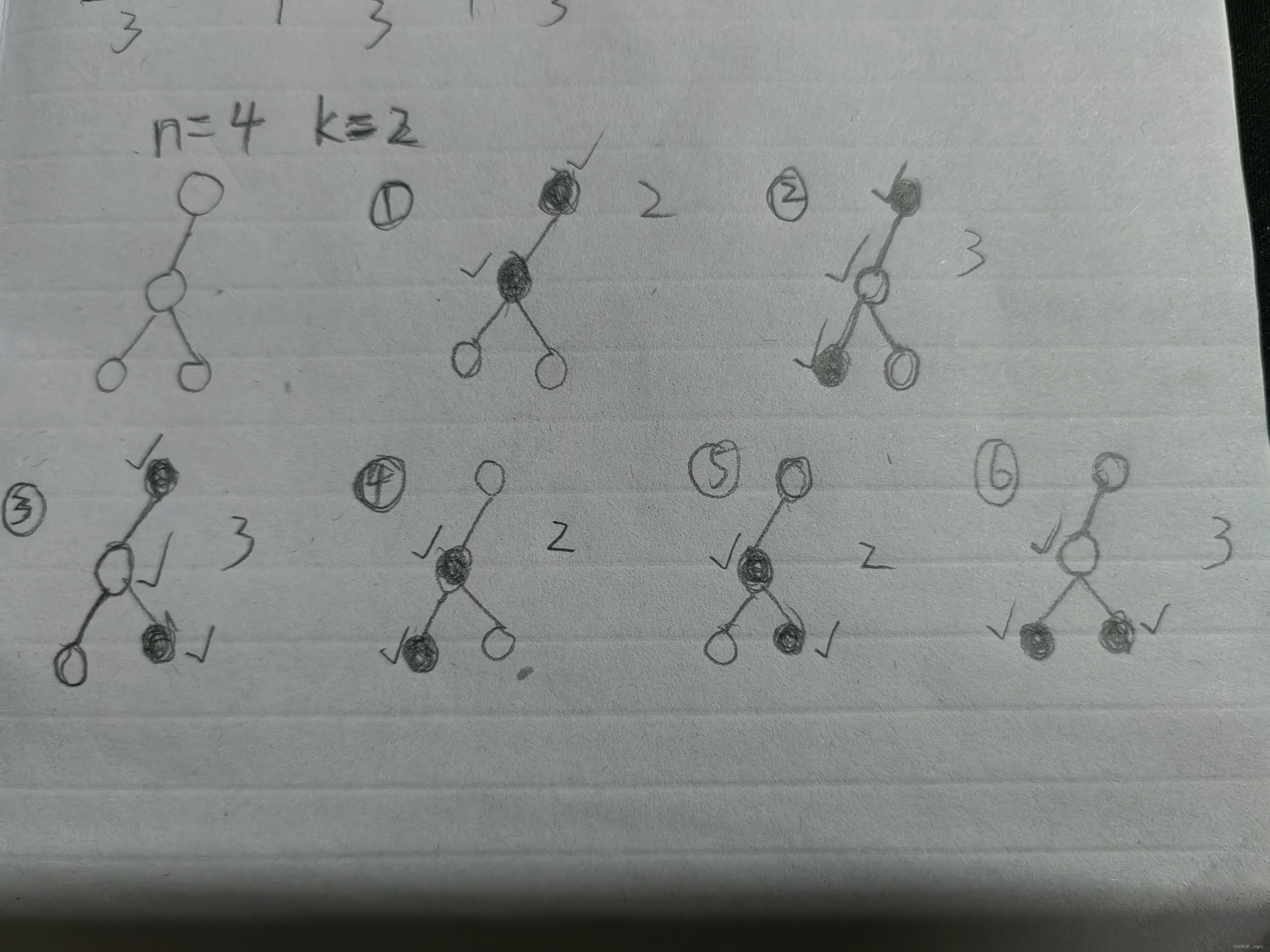

其中黑色结点为特殊结点，可以看出，每种情况都有一个结点的s值不等于k / 2，但是是好结点，所以最后答案加一。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pb push_back
#define fi first
#define se second
#define lson p << 1
#define rson p << 1 | 1
const int maxn = 1e6 + 5, inf = 1e18 + 5, maxm = 4e4 + 5, mod = 1e9 + 7, N = 1e6;
int a[maxn], b[maxn];
// bool vis[maxn];
int n, m;
string s;
vector<int> G[maxn];
int siz[maxn];
int fac[maxn], inv[maxn];int qpow(int a, int b){int res = 1;while(b){if(b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}int C(int n, int m){if(n < m) return 0;return fac[n] * inv[m] % mod * inv[n - m] % mod;
}void dfs(int u, int p){siz[u] = 1;for(auto v : G[u]){if(v == p) continue;dfs(v, u);siz[u] += siz[v];}
}void solve(){int res = 0;int x, q, k;cin >> n >> k;for(int i = 1; i < n; i++){int u, v;cin >> u >> v;G[u].pb(v);G[v].pb(u);}if(k % 2 == 1){cout << 1 << '\n';return;}dfs(1, 1);res = 0;for(int i = 1; i <= n; i++){res = (res + C(siz[i], k / 2) * C(n - siz[i], k / 2) % mod * qpow(C(n, k), mod - 2) % mod) % mod;}res = (res + 1) % mod;cout << res << '\n';
}signed main(){ios::sync_with_stdio(0);cin.tie(0);fac[0] = 1;for(int i = 1; i <= N; i++){fac[i] = fac[i - 1] * i % mod;}inv[N] = qpow(fac[N], mod - 2);for(int i = N - 1; i >= 0; i--){inv[i] = inv[i + 1] * (i + 1) % mod;}int T = 1;// cin >> T;while (T--){solve();}return 0;
}