线段树的定义
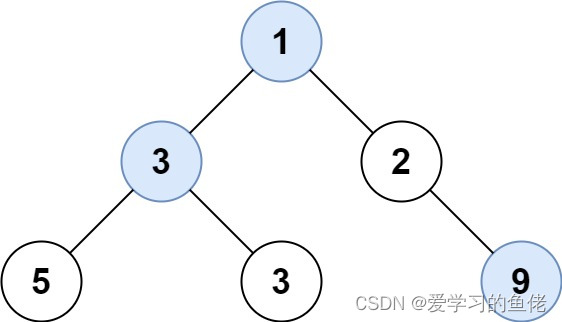
线段树(Segment Tree)是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。使用线段树可以快速地查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。
线段树是一种非常有用的数据结构,其基本思想是通过二分的方式将一个大的区间平均地划分成两个小区间,然后再将每个小区间继续平均划分,直到每个区间只包含一个节点的信息。因此,线段树是一种平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
它的主要作用包括:
- 快速查询:线段树可以高效地查询某个区间内的信息,例如区间和、区间最大值、区间最小值等。通过利用二分查找的思想,线段树可以在O(logN)的时间复杂度内完成这些查询操作。
- 区间修改:除了查询操作外,线段树还可以支持区间修改操作。例如,可以将某个区间内的所有元素都加上一个常数,或者将某个区间内的所有元素都乘以一个常数等。这些操作也可以在O(logN)的时间复杂度内完成。
- 动态维护区间信息:线段树可以动态地维护区间信息,即当区间内的元素发生变化时,线段树可以自动地更新相应的区间信息。这种特性使得线段树在处理动态数据方面非常有用。
需要注意的是,虽然线段树的时间复杂度较低,但是它的空间复杂度较高,因此在实际应用时需要权衡时间和空间的因素来选择合适的数据结构。
图示讲解
区间计算

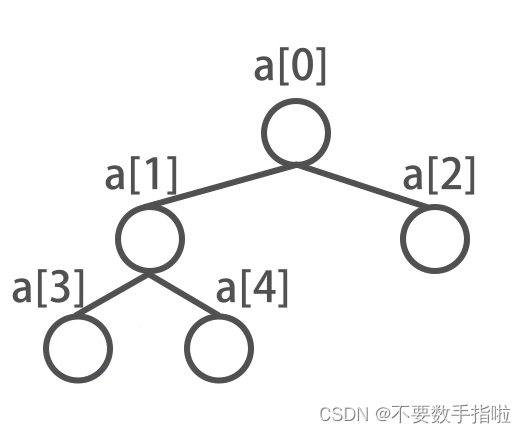
一般通过数组来实现线段树的存储。树的根节点存储在a[0]。
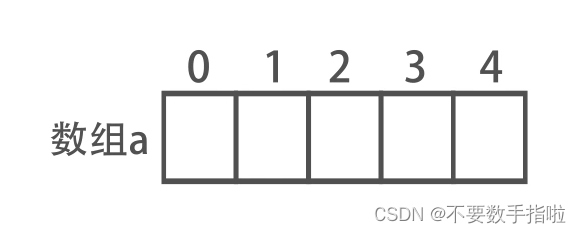
对于任意节点下标i ,都有:

代码实现(示例)
线段树的数据插入
//线段树的数据插入,使用a来存储线段树中的数据
//变量pos对应正在访问的数组下标
//r,l表示当前正在处理的区间的左右端点。
//num为待插入数字
void Tree_insert(vector<int>& a, int pos, int l, int r, int num) {a[pos]++;if (num == r && num == l)return;int mid = (l + r) / 2;//计算区间中点int l_ch = pos * 2 + 1;int r_ch = pos * 2 + 2;if (num <= mid)Tree_insert(a, l_ch, l, mid, num);else Tree_insert(a, r_ch, mid + 1, r, num);
}线段树的查找
int Tree_search(vector<int>& a, int pos, int l, int r, int num) {if (num == r && num == l)return a[pos];int mid = (l + r) / 2;//计算区间中点int l_ch = pos * 2 + 1;int r_ch = pos * 2 + 2;if (num <= mid)return Tree_search(a, l_ch, l, mid, num);else return Tree_search(a, r_ch, mid + 1, r, num);
}线段树的打印
void print_Tree(vector<int>& a, int pos, int l, int r) {printf("[%d %d]a[%d]=%d\n", l, r, pos, a[pos]);if (l == r)return;int mid = (l + r) / 2;//计算区间中点int l_ch = pos * 2 + 1;int r_ch = pos * 2 + 2;print_Tree(a, pos*2+1, l, mid);print_Tree(a, pos*2+2, mid + 1, r);
}