如何量化多样性?答:辛普森多样性指数(Simpson’s Diversity Index)
生物多样性指地球上各种生命的多样性,涵盖所有生命形式,从基因、细菌到所有生态系统,例如森林或珊瑚礁生态系统。
那么如何量化多样性呢?

首先,让我们来理解一下什么是物种多样性。在一个生态系统中,如果有许多不同类型的物种共存,我们就说这个生态系统具有高的物种多样性。相反,如果只有几种物种,那么它的物种多样性就比较低。
我们需要考虑两件事:丰富度(richness)和均匀度(evenness)
- 丰富度:物种数量最直观,样本中的物种越多,样本就越“丰富”;
- 均匀度:相对丰度的一种量化方式,比如一个群落里物种分别是10、11、9个,另一个群落里是10、100、1000个。我们就会感觉第一个群落中好像比第二个更具多样性一些,因为所有物种都是欣欣向荣,而不是差距悬殊。
有了这些基本认识,我们就来看看Simpson’s diversity index的计算公式吧。
D = ∑ i = 1 S ( n i ( n i − 1 ) N ( N − 1 ) ) D = \sum_{i=1}^{S} \left( \frac{n_i(n_i - 1)}{N(N - 1)} \right) D=i=1∑S(N(N−1)ni(ni−1))
其中:
- S是物种的总数;
- n i n_i ni是第i个物种的个体数;
- N是所有物种的总个体数。
Simpson’s diversity index 的值范围在 0 到 1 之间,0 表示无限多样性,1 表示无多样性。这个指数越高,代表生态系统的多样性越低。
下面通过一个例子来感受一下这个公式:
考虑两个群落,而这个体数量加起来都是1000,不过1中比较均匀,2中则不均匀。我们来计算一下Simpson’s diversity index:
| 物种 | 样本 1 | 样本 2 |
|---|---|---|
| 苹果 | 300 | 20 |
| 香蕉 | 335 | 49 |
| 橘子 | 365 | 931 |
| 总计 | 1000 | 1000 |
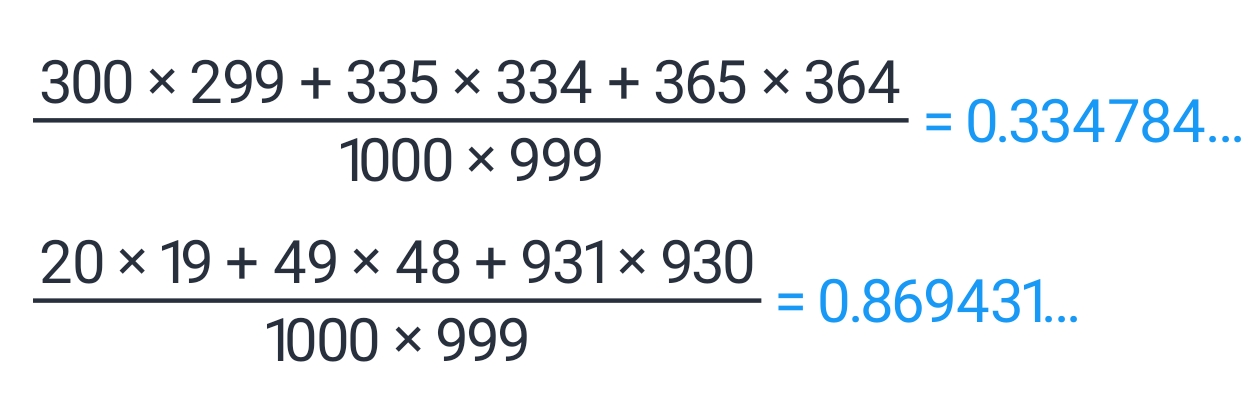
公式果然有用!公式的原理是什么呢?
我们来拆解公式,一部分一部分来看,一步步解释这个公式背后的数学意义以及为什么它可以用来计算多样性。
个体数量的概率分布: 公式中的 n i ( n i − 1 ) N ( N − 1 ) \frac{n_i(n_i - 1)}{N(N-1)} N(N−1)ni(ni−1)部分实际上是描述了从样本中随机选择两个个体,并且它们属于同一物种的概率。
n i N \frac{n_i}{N} Nni就是从N中抽到第i个物种的概率,抽了一个就剩N-1个了,再抽到的概率就是 n i − 1 N − 1 \frac{n_i-1}{N-1} N−1ni−1,相乘就是表示随机选择两个个体,并且它们属于同一物种的概率。
$n_i $表示第 $i 个物种的个体数, 个物种的个体数, 个物种的个体数,N $表示所有物种的总个体数。
物种的相对贡献: 公式中的 $\sum_{i=1}^{S} $部分是对所有物种的个体数的总和进行求和。
可以看到,如果某个物种占比不多,最后式子中的分子就小,但其他的分子就大,因为有平方,总的求和就大,导致D越大,D越大说明物种多样性越小。
D反映了样本多样性。这个数值越接近于 1,代表了样本的多样性越低,因为更多的个体属于少数几个物种。反之,数值越接近于 0,代表了样本的多样性越高,因为个体分布更均匀,属于更多的不同物种。
因此,Simpson’s diversity index 的计算公式背后的数学意义在于,通过考虑样本中每个物种的相对贡献,并量化从样本中随机选择两个个体属于同一物种的概率,我们能够得到一个数值,用来描述样本的多样性水平。
另外,还有两种与 Simpson’s diversity index 密切相关的指标:
- Simpson’s Index of Diversity:1-D ,用来表示样本的多样性。这个指数的值也在 0 到 1 之间,但值越大,样本的多样性越高;
- Simpson’s Reciprocal Index: 1/D,用来表示生态系统的多样性。这个指数的值从 1 开始,最大值为样本中的物种数。
Simpson’s diversity index不仅可以用于生态学研究,还可以应用到其他领域。比如,在医学中,它被用来研究微生物群落的多样性,从而了解健康和疾病之间的关系。此外,在经济学和社会科学中,它也被用来研究不同市场或社区的多样性程度,以及多样性对稳定性和发展的影响。
总的来说,Simpson’s diversity index是一个简单但强大的公式,可以帮助我们理解和量化各种层次的多样性!