定义
二叉搜索树也叫二叉排序树或者二叉查找树。它是一种对排序和查找都很有用的特殊二叉树。
一个二叉搜索树可以为空,如果它不为空,它将满足以下性质:
- 非空左子树的所有键值小于其根节点的键值
- 非空右子树的所有键值都大于其根结点的键值
- 左、右子树都是二叉树
动态查找
查找操作Find
在二叉搜索树中查找关键字为X的结点,返回其所在结点的地址。查找过程如下:
- 查找从树的根节点开始,若树为空,返回NULL
- 搜索树非空,则根节点关键字和X比较,依据结果,需要进行不同的处理
若根节点键值小于X,在根节点右子树中查找
若根节点的键值大于X,在根节点的左子树中查找
若两者比较结果相等,搜索完成。
递归代码
Position Find_RE(BinTree BT, ElementType X) {if (!BT) {return NULL;}if (X > BT->Data) {return Find_RE(BT->Right, X);}else if(X < BT->Data){return Find_RE(BT->Left, X);}else{return BT;}
}
迭代函数
Position Find_D(BinTree BT, ElementType X) {BinTree T = BT;while (T) {if (T->Data > X) {T = T->Left;}else if (T->Data < X) {T = T->Right;}else{return T;}}
}
查找最大和最小元素
根据二叉搜索树的性质,最大元素一定在最右分支的尾端,最小元素一定在最左分支的尾端。
递归函数
Position FindMin(BinTree BT) {if (!BT) {return NULL;}else if(!BT->Left){return BT;}else{return FindMin(BT->Left);}
}
迭代函数
Position FindMinD(BinTree BT) {BinTree T = BT;while (T->Left) {T = T->Left;}return T;
}
找最大值只需要把left换成right
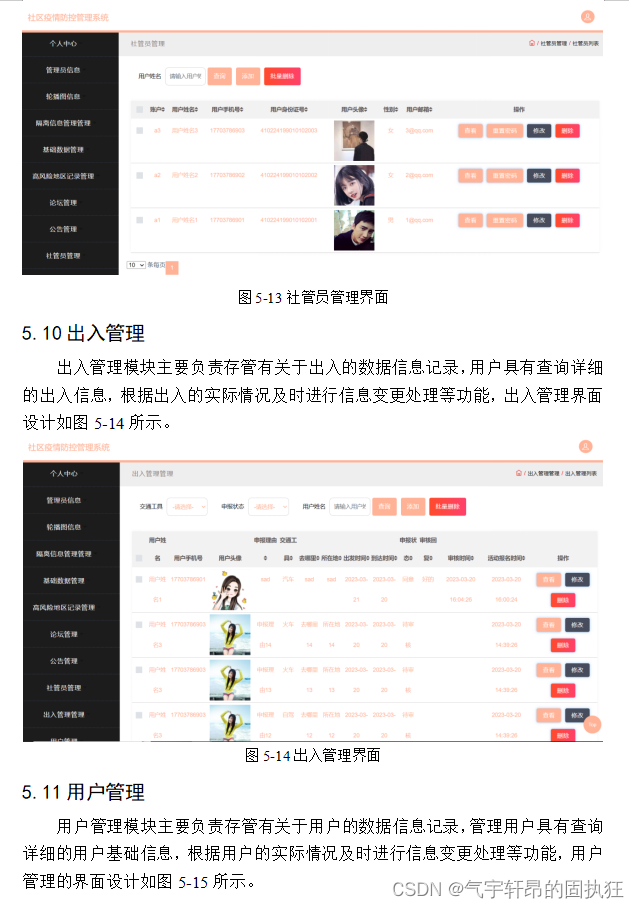
插入
BinTree Insert(BinTree BT, ElementType X) {if (!BT) {BT = (BinTree)malloc(sizeof(struct TNode));BT->Data = X;BT->Left = BT->Right = NULL;}else {if (X > BT->Data) {BT->Right = Insert(BT->Right, X);}else if (X < BT->Data) {BT->Left = Insert(BT->Left, X);}}return BT;
}
删除
二叉搜索树的删除比较复杂,需要考虑节点的位置
- 叶结点
可以直接删除,将其父节点指针置空即可。 - 只有一个孩子结点
要修改其父节点的指针,指向要删除结点的孩子结点。 - 有左、右两颗树
究竟用哪颗子树的根结点来填充删除节点的位置?有两种选择方式:选择左子树的最大元素,或者选择右子树的最小元素。无论哪种方式,最后被选择的结点必定最多只有一个孩子。
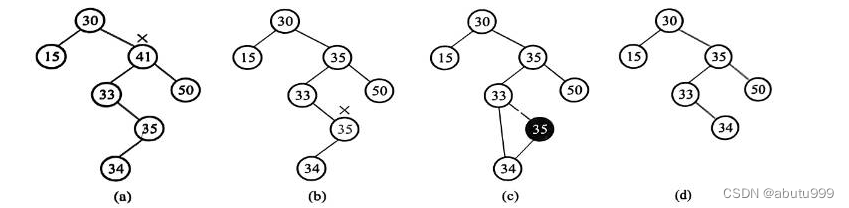
采用右子树的最小元素的删除代替策略。
代码思路: 先找到要删除元素的位置,若其具有左右子树,找到该位置的右子树里面的最小元素,赋值到该位置上,在其右子树中删除最小元素(递归调用),若只有一个子树或者没有,易操作。
BinTree DeleteBT(BinTree BT, ElementType X) {Position p;if (!BT) {printf("can't find the node\n");}else {if (X > BT->Data) {BT->Right = DeleteBT(BT->Right, X);}else if (X < BT->Data) {BT->Left = DeleteBT(BT->Left, X);}else {if (BT->Left && BT->Right) {//FIND THE Min OF Right TREEp = FindMin(BT->Right);BT->Data = p->Data;BT->Right = DeleteBT(BT->Right, p->Data);}else {p = BT;if (!BT->Left) {BT = BT->Right;}else { BT = BT->Left; }free(p);}}}return BT;
}