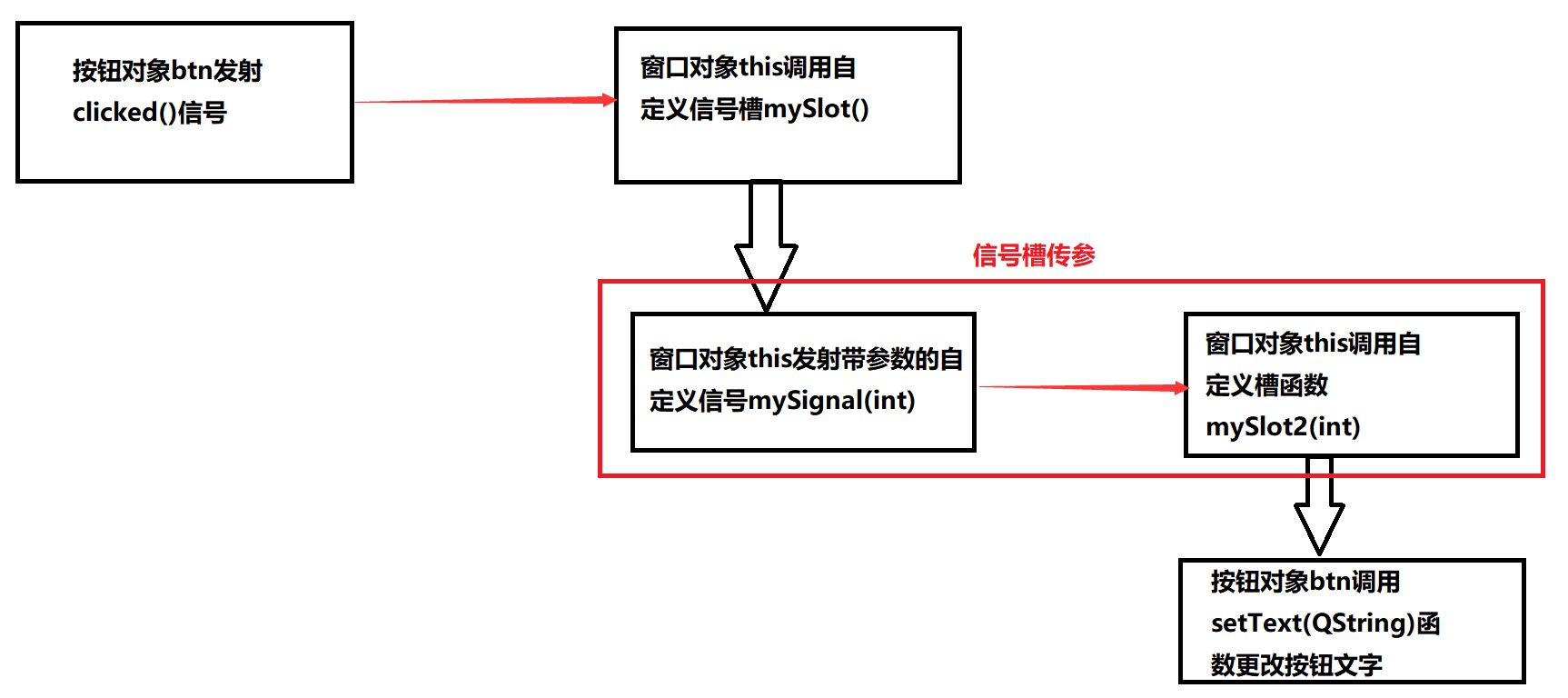
庖丁解牛-二叉树的遍历-编程知识

庖丁解牛-二叉树的遍历

在这里插入图片描述

〇、前言

01 文章内容

一般提到二叉树的遍历，我们是在说
- 前序遍历、中序遍历、后序遍历和层序遍历
或者说三序遍历+层序遍历，毕竟三序和层序的遍历逻辑相差比较大
下面讨论三序遍历的递归方法、非递归方法和非递归迭代的统一方法
然后再讨论一下层序的一般迭代方法（通过队列）

02 力扣网址

144. 二叉树的前序遍历 - 力扣（LeetCode）
94. 二叉树的中序遍历 - 力扣（LeetCode）
145. 二叉树的后序遍历 - 力扣（LeetCode）

一、前序遍历

01 递归实现

递归的基本逻辑是比较简单的，但是注意根据题目的需求不同，实现方式是存在差异的
如果题目要求主函数返回一个结果列表，那么就要构造一个辅助函数来帮助实现
如果题目只要求函数打印前序遍历的序列，那么一个函数就足够了

(1) 返回列表版本1

返回列表版本：辅助函数携带结果列表

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderTraversalHelper(root,result);return result;}
void preorderTraversalHelper(TreeNode root,List<Integer> result){if(root == null) return;result.add(root.val);inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);return;
}

(2) 返回列表版本2

返回列表版本：设置全局变量

List<Integer> result = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversalHelper(TreeNode root){if(root == null) return;result.add(root.val);inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);return;
}

(3) 纯真打印版本

public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversal(TreeNode root){if(root == null) return;System.out.print(root.val);inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);return;
}

(4) 面向对象版本

class Solution {class TraverBox{List<Integer> list;TraverBox(){list = new ArrayList<>();}void preorderTraversalHelper(TreeNode root) {list.add(root.val);}void preTraverHelper(TreeNode root) {if(root == null) return;list.add(root.val);preTraverHelper(root.left);preTraverHelper(root.right);}List<Integer> preTraver(TreeNode root) {preTraverHelper(root);return list;}}public List<Integer> preorderTraversal(TreeNode root) {TraverBox tox = new TraverBox();tox.preTraver(root);return tox.list;}
}

02 非递归实现

(1) 一般迭代法

(2) 统一迭代法

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root); //将根结点入栈while(!stack.isEmpty()){subRoot = stack.pop(); //弹出获取栈顶结点if(subRoot != null){//===右===if(subRoot.right != null){// 添加右结点（空结点不入栈）stack.push(subRoot.right);}//===左===if(subRoot.left != null){// 添加左节点（空结点不入栈）stack.push(subRoot.left);}//===中===stack.push(subRoot); // 添加中结点stack.push(null); // 中结点访问过，但是还没有处理，加入空结点做为标记。}else{ // 只有遇到空结点的时候，才将下一个结点放进结果集result.add(stack.pop().val); //重新取出栈中元素，加入到结果集}}return result;
}

二、中序遍历

01 递归实现

(1) 返回列表版本1

返回列表版本：辅助函数携带结果列表

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderTraversalHelper(root,result);return result;}
void preorderTraversalHelper(TreeNode root,List<Integer> result){if(root == null) return;inorderTraversalHelper(root.left,result);result.add(root.val);inorderTraversalHelper(root.right,result);return;
}

(2) 返回列表版本2

返回列表版本：设置全局变量

List<Integer> result = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversalHelper(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);result.add(root.val);inorderTraversalHelper(root.right,result);return;
}

(3) 纯真打印版本

void preorderTraversal(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);System.out.print(root.val);inorderTraversalHelper(root.right,result);return;
}

02 非递归实现

(1) 一般迭代法

void inOrderNonRecur(){Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = root;if (subRoot != null) {while (!stack.isEmpty() || subRoot != null) {if (subRoot != null) {stack.push(subRoot);subRoot = subRoot.left;} else {subRoot = stack.pop();System.out.print("【"+subRoot.val+"】");subRoot = subRoot.right;}}}
}

(2) 统一迭代法

带注释版本

public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root);while (!stack.isEmpty()) {subRoot = stack.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中if (subRoot != null) {//===右===if(subRoot.right != null){// 添加右节点（空节点不入栈）stack.push(subRoot.right);}//===中===stack.push(subRoot); // 添加中节点stack.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。//===左===if(subRoot.left != null){// 添加左节点（空节点不入栈）stack.push(subRoot.left);}} else { // 只有遇到空节点的时候，才将下一个节点放进结果集result.add(stack.pop().val); // 加入到结果集}}return result;
}

无注释版本

public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root);while (!stack.isEmpty()) {subRoot = stack.pop();if (subRoot != null) {if(subRoot.right != null) stack.push(subRoot.right);stack.push(subRoot);stack.push(null);if(subRoot.left != null) stack.push(subRoot.left);} else {result.add(stack.pop().val);}}return result;
}

三、后序遍历

01 递归实现

(1) 返回列表版本1

返回列表版本：辅助函数携带结果列表

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderTraversalHelper(root,result);return result;}
void preorderTraversalHelper(TreeNode root,List<Integer> result){if(root == null) return;inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);result.add(root.val);return;
}

(2) 返回列表版本2

返回列表版本：设置全局变量

List<Integer> result = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversalHelper(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);result.add(root.val);return;
}

(3) 纯真打印版本

void preorderTraversal(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);System.out.print(root.val);return;
}

02 非递归实现

(1) 一般迭代法

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root != null) {Stack<TreeNode> stack = new Stack<TreeNode>();stack.push(root);TreeNode subRoot = null;while (!stack.isEmpty()) {subRoot = stack.peek();if (subRoot.left != null && root != subRoot.left && root != subRoot.right) {stack.push(subRoot.left);} else if (subRoot.right != null && root != subRoot.right) {stack.push(subRoot.right);} else {result.add(stack.pop().val);root = subRoot;}}}return result;
}

(2) 双栈迭代法

public List<Integer> postOrderNonRecurByTwoStack(){List<Integer> result = new ArrayList<>();TreeNode subRoot = root;if (subRoot != null) {Stack<TreeNode> s1 = new Stack<TreeNode>();Stack<TreeNode> s2 = new Stack<TreeNode>();s1.push(subRoot);while (!s1.isEmpty()) {subRoot = s1.pop();s2.push(subRoot);if (subRoot.left != null) {s1.push(subRoot.left);}if (subRoot.right != null) {s1.push(subRoot.right);}}while (!s2.isEmpty()) {result.add(s2.pop().val);}}
}

(3) 统一迭代法

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root); //将根结点入栈while(!stack.isEmpty()){subRoot = stack.pop(); //弹出获取栈顶结点if(subRoot != null){//===中===stack.push(subRoot); // 添加中结点stack.push(null); // 中结点访问过，但是还没有处理，加入空结点做为标记。//===右===if(subRoot.right != null){// 添加右结点（空结点不入栈）stack.push(subRoot.right);}//===左===if(subRoot.left != null){// 添加左节点（空结点不入栈）stack.push(subRoot.left);}}else{ // 只有遇到空结点的时候，才将下一个结点放进结果集result.add(stack.pop().val); //重新取出栈中元素，加入到结果集}}return result;
}

四、层序遍历

01 不分层输出

class Solution {public int[] levelOrder(TreeNode root) {//if(root == null) return new int[]{};ArrayList<Integer> result = new ArrayList<Integer>();Queue<TreeNode> queue = new LinkedList<TreeNode>();TreeNode subRoot = new TreeNode();if(root != null) queue.offer(root);while(!queue.isEmpty()){subRoot = queue.poll();result.add(subRoot.val);if(subRoot.left != null) queue.add(subRoot.left);if(subRoot.right != null) queue.add(subRoot.right);}int[] dest = new int[result.size()];for(int i = 0 ; i < result.size() ; i++){dest[i] = result.get(i);}return dest;}
}

02 分层输出

public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ret = new ArrayList<List<Integer>>();if (root == null) {return ret;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> level = new ArrayList<Integer>();int currentLevelSize = queue.size();for (int i = 1; i <= currentLevelSize; ++i) {TreeNode node = queue.poll();level.add(node.val);if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}ret.add(level);}return ret;
}