堆/堆排序（C/C++）-编程知识

本篇文章将会较为全面的介绍堆的概念以及实现堆两个重要算法：向上调整算法和向下调整算法。接着实现了堆排序。

若想查看对应位置，可直接按照以下目录进行查看：

目录

1.堆的概念及结构

2.堆的实现

2.1 堆的向上调整算法

2.2 堆的向下调整算法

2.3 堆的插入

2.4 堆的删除

2.5 堆的实现

3.堆排序

1.堆的概念及结构

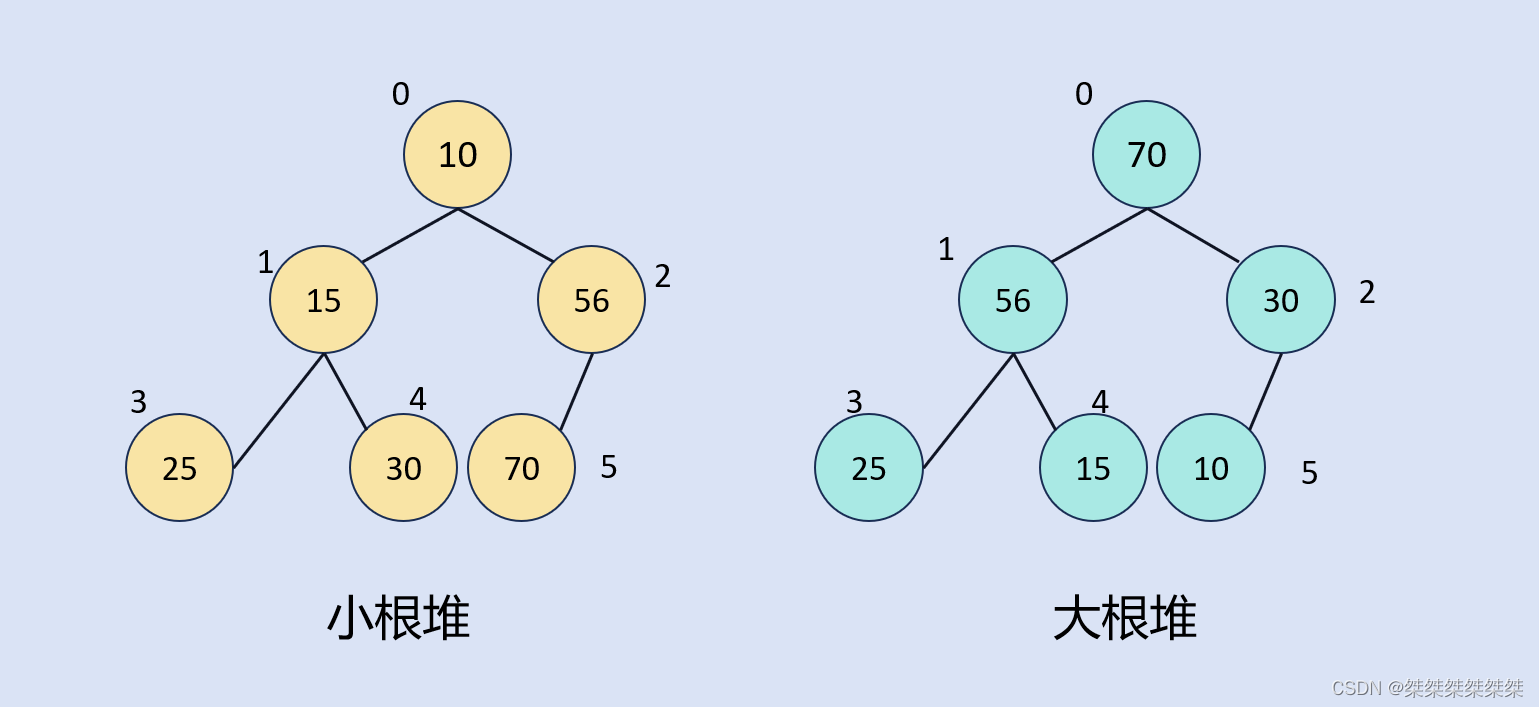
概念：若一个关键码的集合 $K=\left\{ k_0,k_1,k_2,k_3,...,k_{n-1} \right\}$ ，把它的所有元素按照完全二叉树的顺序存储方式存储在一个一维数组中，并满足：sss且xxx（xxx且zzzz），则称为小堆（大堆）。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

性质：1.堆中的某个节点的值总是不大于或不小于其父节点的值；

2.堆总是一颗完全二叉树；

3.堆中父节点的关系与孩子节点的关系为： $leftchild_k=parent_{2\times i+1},rightchild_k=parent_{2\times i+2}\,\,$

堆的结构如下：

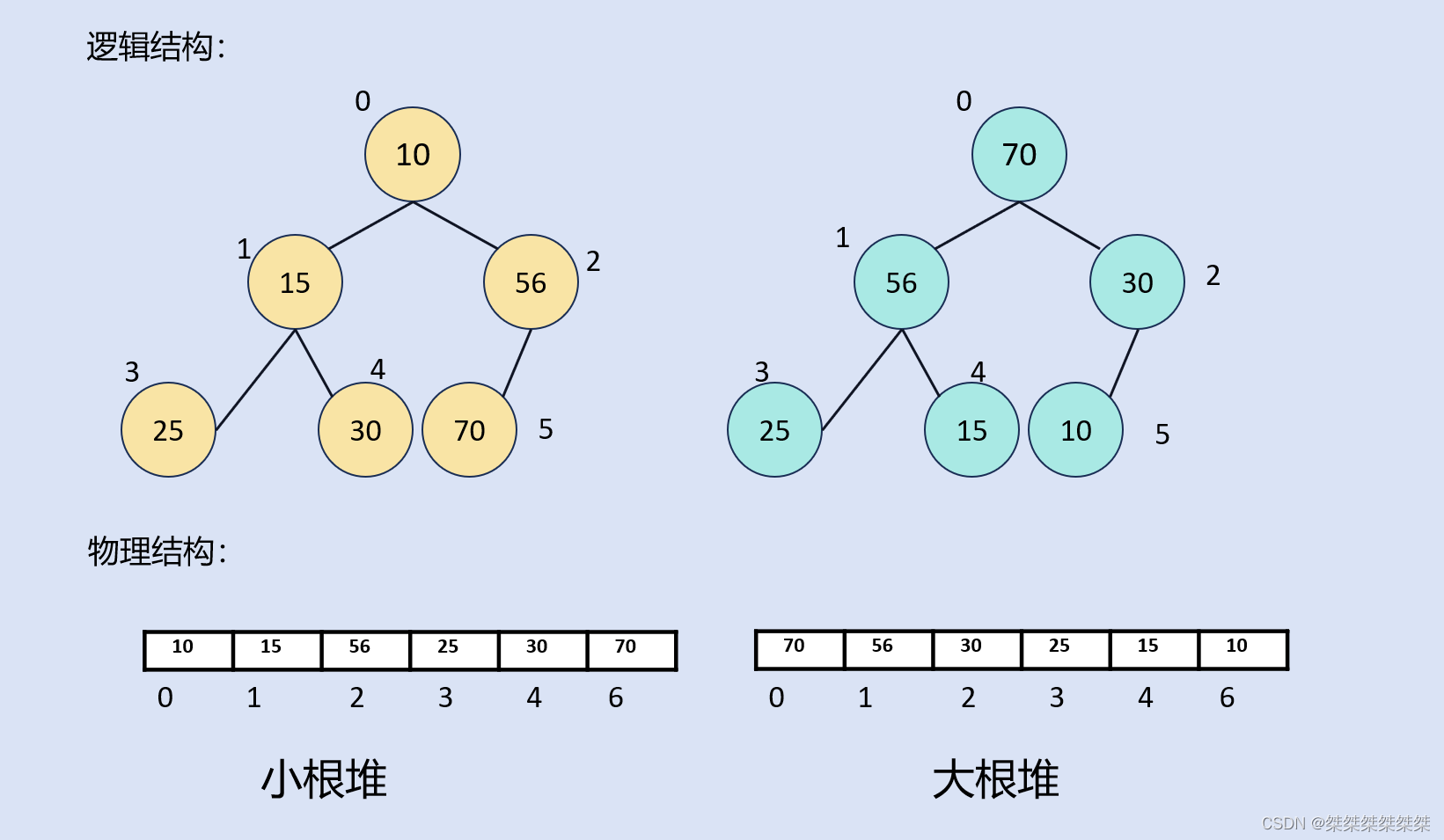
堆的存储结构：在数据结构中，对于二叉树的存储结构一般可以分为链式存储、顺序表存储；同样，对于堆的存储我们也可以选择链式存储和顺序表存储，但我们需要从中选出最优的存储结构。对于满二叉树和完全的二叉树的顺序表存储结构对于整个顺序表都可以将其存储满，并且下标的变化便于我们在堆中添加数据和调整数据。所以我们使用顺序表来存储堆。如下：

2.堆的实现

堆的实现主要的两个点为堆的建立和堆的调整，其中的主要思想为堆的向上调整算法和向下调整算法，具体的实现将会在下面实现。

2.1 堆的向上调整算法

堆的向上调整发算法是实现堆的插入核心算法。

对于堆的建立，假设我们将一组数据一个一个的加入到堆中，那么我们需要在每一个元素入堆时都要进行调整，我们将加入的元素存入到顺序表的最后，然后利用双亲结点和孩子结点之间的关系来判断是否需要调整，知道调整到根节点为止。对于此算法思想既可以使用递归算法，也可以使用循环算法，在这里我们使用循环算法，如下：

具体的实现算法如下：
void Swap(HPDataType* p1, HPDataType* p2) {HPDataType* tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0) {//建立小堆，若建大堆，将 < 改为 >if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}

2.2 堆的向下调整算法

向下调整算法是堆删除堆顶元素的核心算法。

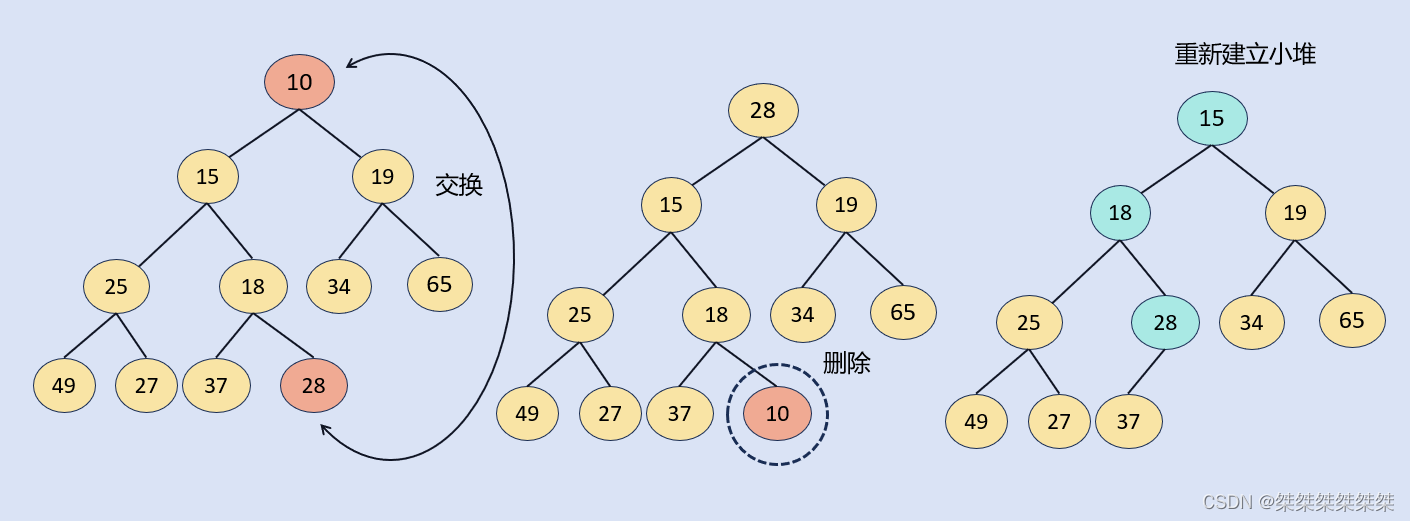
向下调整算法的主要作用为：当我们需要将堆顶的元素弹出时，将整个堆进行维护，建立一个新的堆。其主要思路是将当前元素的孩子结点与双亲结点进行比较，但是此时双亲节点的孩子节点有两个，我们需要找出最合适的那一个，比如：建小堆则找出最小的孩子结点，建大堆则找出最大的孩子结点。然后将孩子结点与双亲结点进行交换，以此迭代，直到迭代到叶子结点。

图示如下：

以建小堆的算法为例，算法如下：
//建小堆的向下调整算法
void AdjustDown(HPDataType* a, int size, int parent) {//左孩子结点与双亲结点的关系int child = parent * 2 + 1;//假若右孩子比左孩子更小，则将child变量加一。child + 1 <size 用于保证不会越界//若建大堆，改为if ((a[child + 1] > a[child]) && (child + 1) < size)if ((a[child + 1] < a[child]) && (child + 1) < size) {++child;}//当child>=size时表示已经到达叶子结点跳出循环while (child<size) {//双亲结点大于孩子结点交换//若建大堆，改为if (a[parent] < a[child])if (a[parent] > a[child]) {Swap(&a[parent], &a[child]);//进行迭代parent = child;child = parent * 2 + 1;if ((a[child + 1] < a[child]) && (child + 1) < size) {++child;}}//若双亲结点不在大于孩子结点，说明已经迭代结束，不在需要继续进行迭代else {break;}}
}

2.3 堆的插入

堆的插入就是在堆中插入元素，直接在堆的顺序存储的最后一个位置插入元素，然后调用向上调整算法，对堆进行维护。具体算法如下：

void HeapPush(Heap* php, HPDataType x) {assert(php);//判断顺序表的容量，是否需要扩容if (php->capacity == php->size) {int newCapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);HPDataType* tmp = (HPDataType*)realloc(php->a,newCapacity * sizeof(HPDataType));if (tmp == NULL) {perror("realloc failed:");exit(1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;//调用向上调整算法AdjustUp(php->a, php->size);php->size++;
}

2.4 堆的删除

堆的删除就是将堆顶的元素弹出，然后使用向下调整算法对堆进行维护。具体算法如下：
void HeapPop(Heap* php) {assert(php);assert(php->a > 0);//将最后一个元素调换在堆顶元素位置，便于进行向下调整算法php->a[0] = php->a[php->size - 1];php->size--;//调用向下调整算法AdjustDown(php->a, php->size, 0);
}

2.5 堆的实现

以下为堆的所有代码：

Heap.h

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>typedef int HPDataType;typedef struct Heap {HPDataType* a;int size;int capacity;
}Heap;void HeapInit(Heap* php);
void HeapDestroy(Heap* php);
void HeapPush(Heap* php, HPDataType x);
void HeapPop(Heap* php);
HPDataType HeapTop(Heap* php);
int HeapSize(Heap* php);
bool HeapEmpty(Heap* php);void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int size, int parent);
void Swap(HPDataType* p1, HPDataType* p2);

Heap.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"void HeapInit(Heap* php) {assert(php);php->a = NULL;php->capacity = 0;php->size = 0;
}void HeapDestroy(Heap* php) {assert(php);free(php->a);php->capacity = php->size = 0;
}void Swap(HPDataType* p1, HPDataType* p2) {HPDataType* tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0) {//建立小堆if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}void HeapPush(Heap* php, HPDataType x) {assert(php);if (php->capacity == php->size) {int newCapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);HPDataType* tmp = (HPDataType*)realloc(php->a,newCapacity * sizeof(HPDataType));if (tmp == NULL) {perror("realloc failed:");exit(1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;AdjustUp(php->a, php->size);php->size++;
}//建小堆的向下调整算法
void AdjustDown(HPDataType* a, int size, int parent) {//左孩子结点与双亲结点的关系int child = parent * 2 + 1;//假若右孩子比左孩子更小，则将child变量加一。if ((a[child + 1] < a[child]) && (child + 1) < size) {++child;}//当child>=size时表示已经到达叶子结点跳出循环while (child < size) {//双亲结点大于孩子结点交换if (a[parent] > a[child]) {Swap(&a[parent], &a[child]);//进行迭代parent = child;child = parent * 2 + 1;if ((a[child + 1] < a[child]) && (child + 1) < size) {++child;}}//若双亲结点不在大于孩子结点，说明已经迭代结束，不在需要继续进行迭代else {break;}}
}void HeapPop(Heap* php) {assert(php);assert(php->a > 0);php->a[0] = php->a[php->size - 1];php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(Heap* php) {assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(Heap* php) {assert(php);return php->size;
}bool HeapEmpty(Heap* php) {assert(php);return php->size == 0;
}

test.c

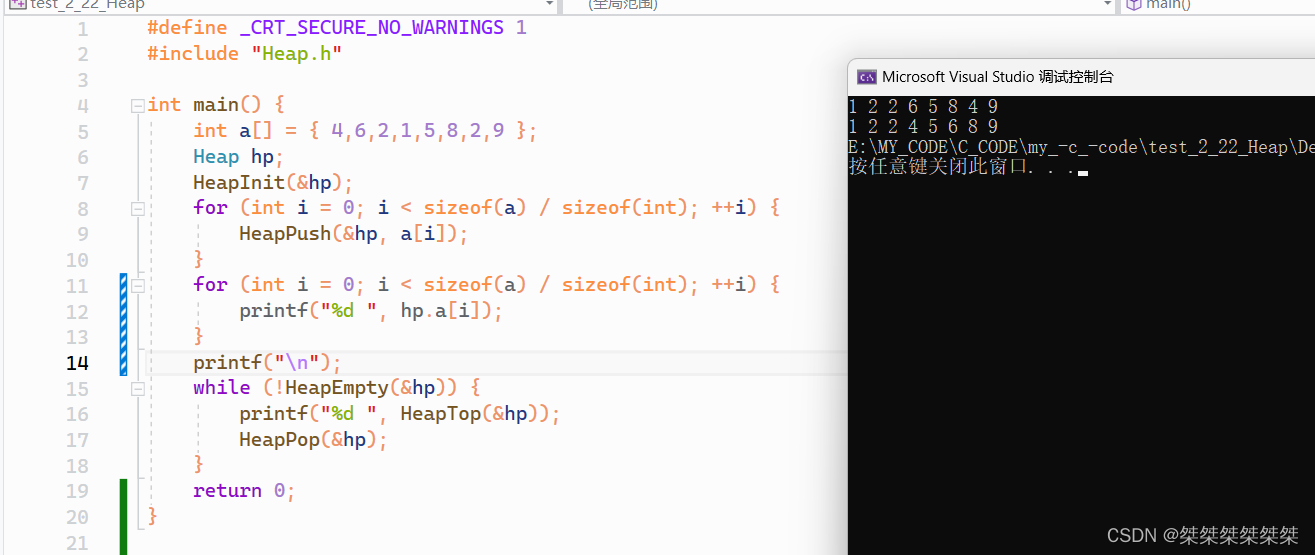
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"int main() {int a[] = { 4,6,2,1,5,8,2,9 };Heap hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); ++i) {HeapPush(&hp, a[i]);}for (int i = 0; i < sizeof(a) / sizeof(int); ++i) {printf("%d ", hp.a[i]);}printf("\n");while (!HeapEmpty(&hp)) {printf("%d ", HeapTop(&hp));HeapPop(&hp);}return 0;
}

测试结果：

3.堆排序

在上文中，已经较为介绍了堆的实现，现在实现堆的应用之一：堆排序。下午以降序排序为例进行介绍。

对于堆的作用，我们在上文可以很清楚的得知，在小堆中，堆顶元素就是整个数据中最小的数据，但是对于后面的数据，并不一定呈现有序的方式排列，所以只能保证小堆的堆顶元素为最小值。所以若要将一组数据进行排序，其主要思路是先将其建堆，然后将堆顶元素放在数据最后，在将前n - 1个数据进行建堆，然后放到第n - 1个位置，以此循环递归，直至将数据排列完成。

对于堆排序的排序原则为，降序排序为建大堆，升序排序为建小堆。以降序排序为例：当我们建立出小顶堆时，可以得出整列数据中最小的值，然后将最小值一致顺序表的最后位置，接着对前面的数据建堆，然后置换位置，以此迭代。若使用建大堆进行降序排列呢？每一次可以得到一个最大的值，然后将其放在第一个位置，对2 ~ n个位置的元素进行建堆。理论上可以，但是真正实行起来，对于第一个位置后的元素进行建堆这个步骤就会很麻烦，所以我们使用小堆进行降序排序。

升序排序思路和上面基本一致，只有建小堆和大堆的区别。具体代码如下：
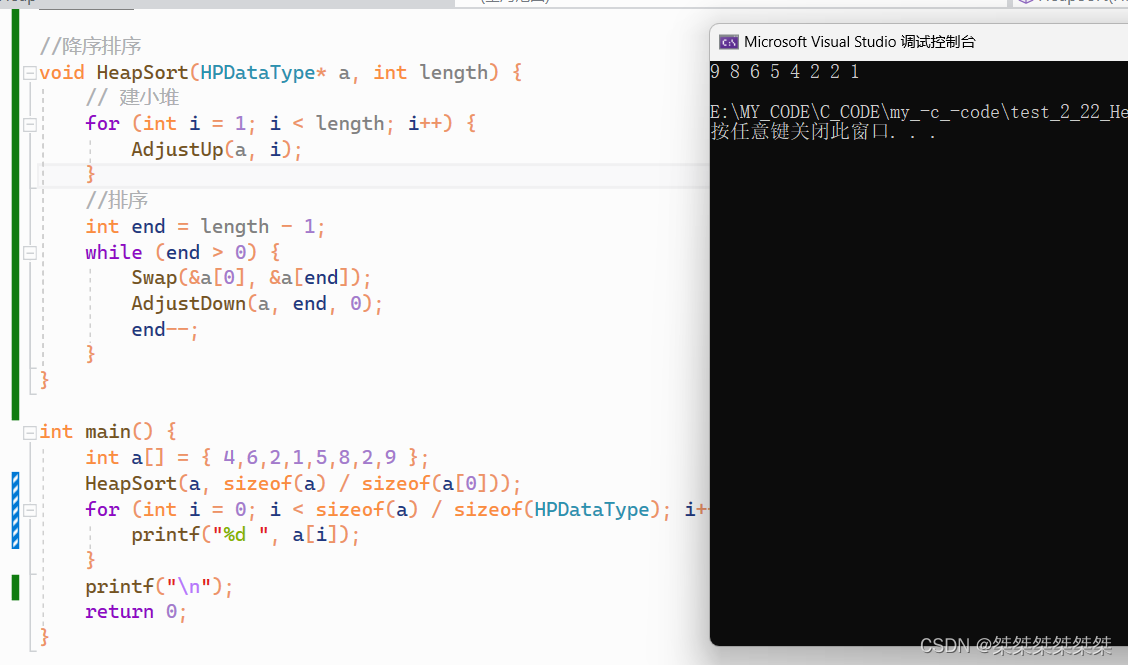
//降序排序
void HeapSort(HPDataType* a, int length) {// 建小堆for (int i = 1; i < length; i++) {AdjustUp(a, i);}//排序int end = length - 1;while (end > 0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}int main() {int a[] = { 4,6,2,1,5,8,2,9 };HeapSort(a, sizeof(a) / sizeof(a[0]));for (int i = 0; i < sizeof(a) / sizeof(HPDataType); i++) {printf("%d ", a[i]);}printf("\n");return 0;
}
测试结果：