二叉树创建字符串

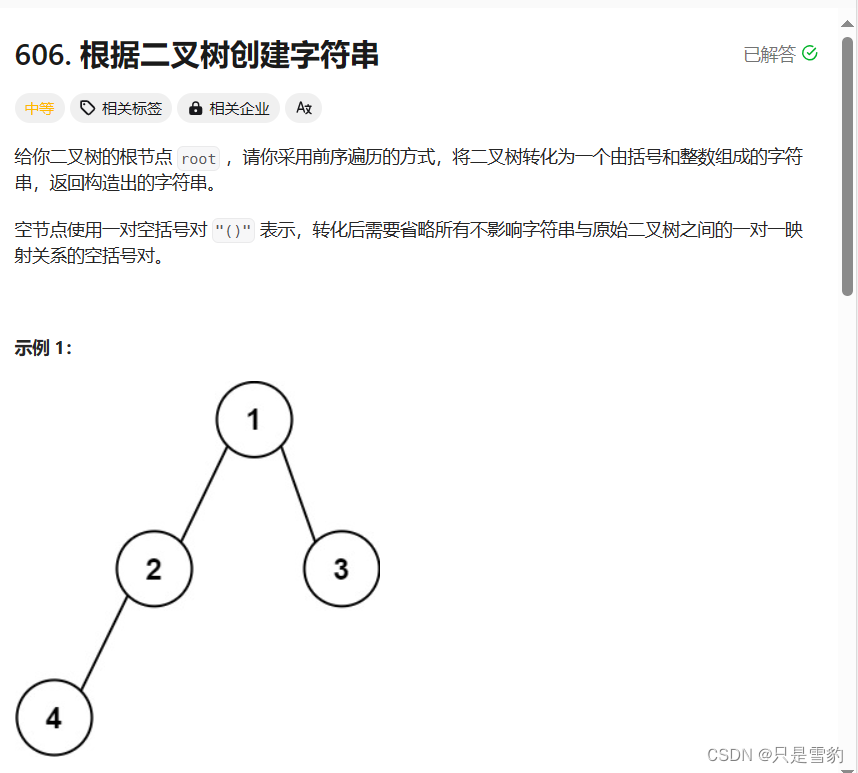
我们首先进行题目的解读：
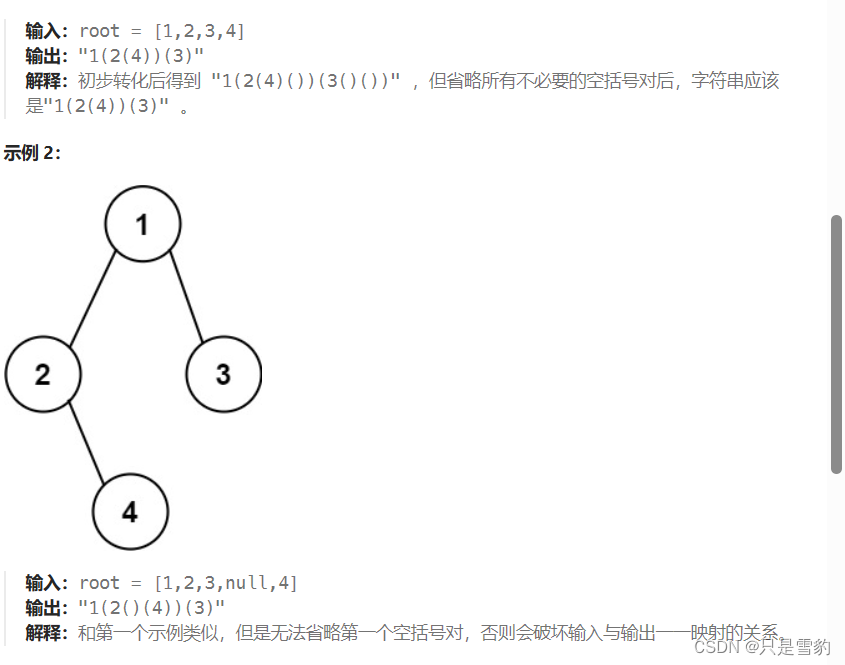
大概意思就是用（）把每个节点的值给括起来，然后再经过一系列的省略的来得到最后的结果

大家仔细观察题目给出的列子就可以发现，其实这个题目可以大致分为三种情况：

1 节点的左孩子和右孩子都在，不能省略括号
2 节点没有左孩子只有右孩子，不能省略括号
3 节点没有右孩子只有左孩子，可以省略这个空节点的括号，用来区分第二种情况，保证了一个字符串只能对应一个二叉搜索树

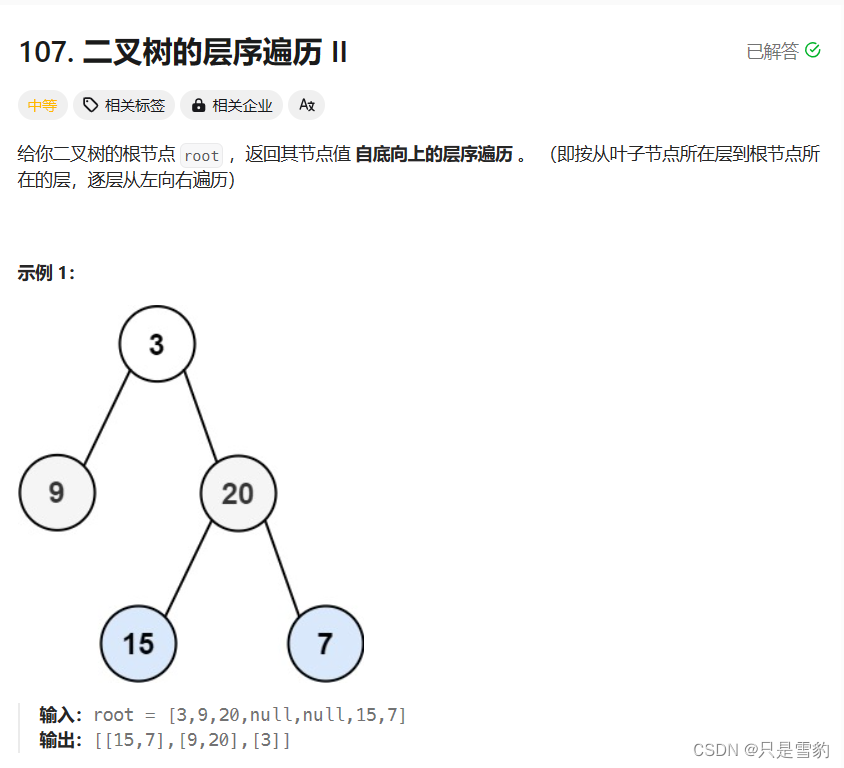
就比如例1：

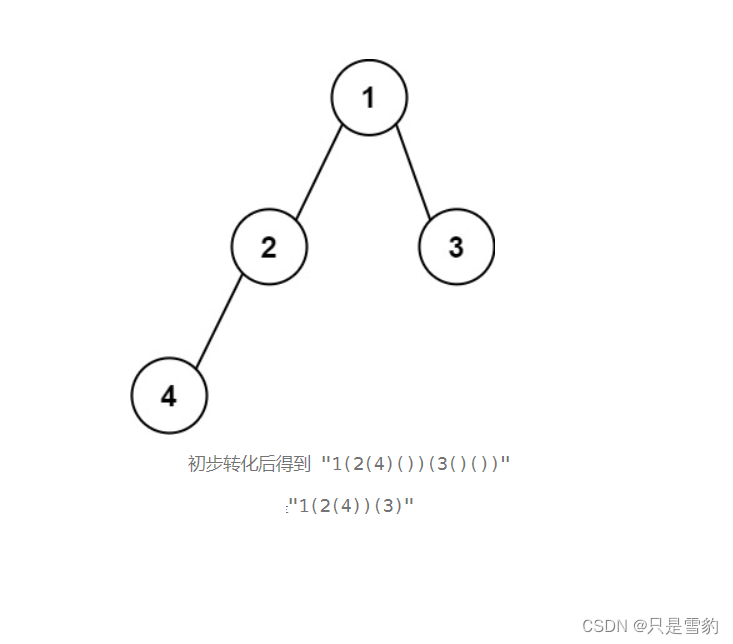
例子中给出的初步转化的字符串是没有经过省略的，其实4后面还要加上两个空括号才完美，这里题目有一点小误差

就比如节点2他的右孩子节点是空的，所以那个括号就要省略，4和3的两个括号都省略，就可以得到最后的结果了

代码如下：
我们首先定义一个字符串，如果根节点root为空，就直接返回这个空字符串，不为空先＋=root内存储的val
如果root的左孩子节点或者root的右孩子节点不为空的话，就要把root的左孩子节点的val用括号括起来，就算左孩子为空这个括号也不能省略
如果root的右孩子不为空就要把root的右孩子用括号括起来，最后 返回时str即可

class Solution {
public:string tree2str(TreeNode* root) {string str;if(root==nullptr)return str;str+=to_string(root->val);if(root->left||root->right){ str+='(';str+=tree2str(root->left);str+=')';}if(root->right){str+='(';str+=tree2str(root->right);str+=')';}return str;}
};

二叉树的分层遍历

正

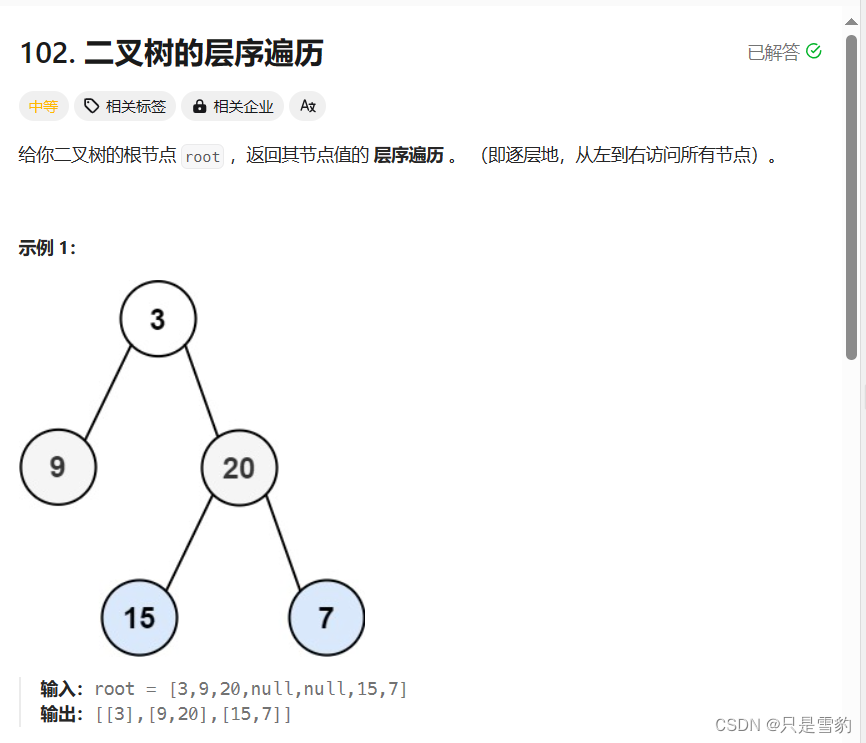
这个题目是一个典型的vector里面套vector(int)的题目，他最后返回的是双层结构

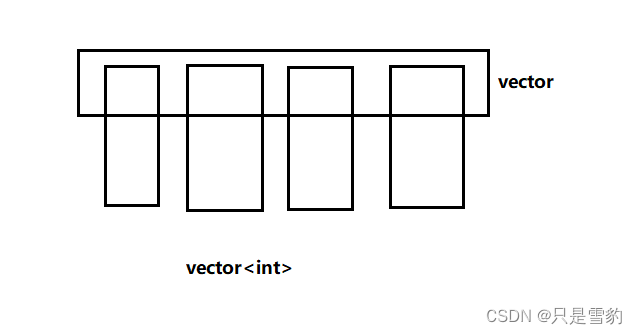
我们可以用到一个队列，这个队列用来存放节点，而双层的vector容器就用来存放层序遍历节点的val，最后返回

我们先将root节点放进队列，然后当他出来后，将他的左右孩子节点放入队列，只要队列不为空不就继续

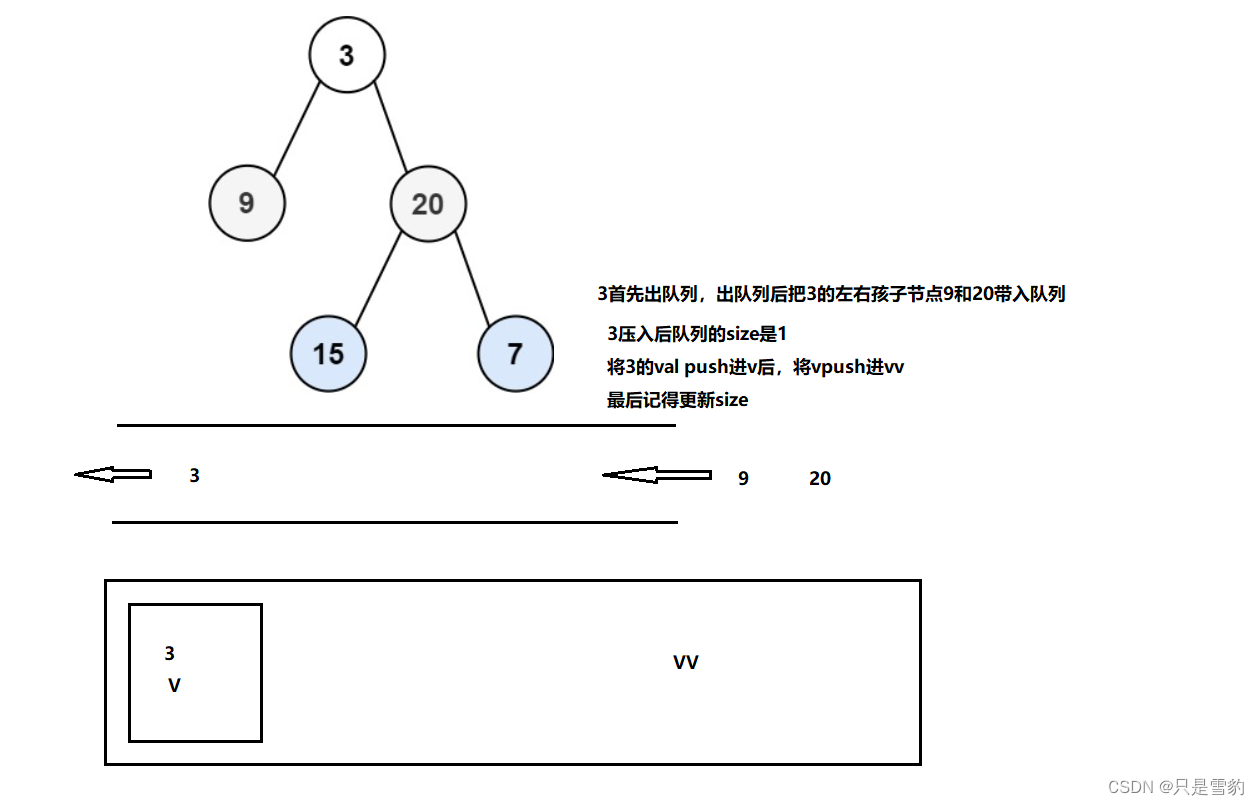
完整代码如下：

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> q;vector<vector<int>> vv;if(root==nullptr)return vv;int levelsize=0;q.push(root);levelsize=q.size();while(!q.empty()){vector<int> v;while(levelsize--){TreeNode* node=q.front();q.pop();v.push_back(node->val);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}vv.push_back(v);levelsize=q.size();}return vv;}
};

反

自底向上的层序遍历，我们就偷懒直接用上面的代码，用一个reverse函数反转即可：

将vv的迭代器反转

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> q;vector<vector<int>> vv;if(root==nullptr)return vv;int levelsize=0;q.push(root);levelsize=q.size();while(!q.empty()){vector<int> v;while(levelsize--){TreeNode* node=q.front();q.pop();v.push_back(node->val);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}vv.push_back(v);levelsize=q.size();}reverse(vv.begin(),vv.end());return vv;}
};

最近公共祖先

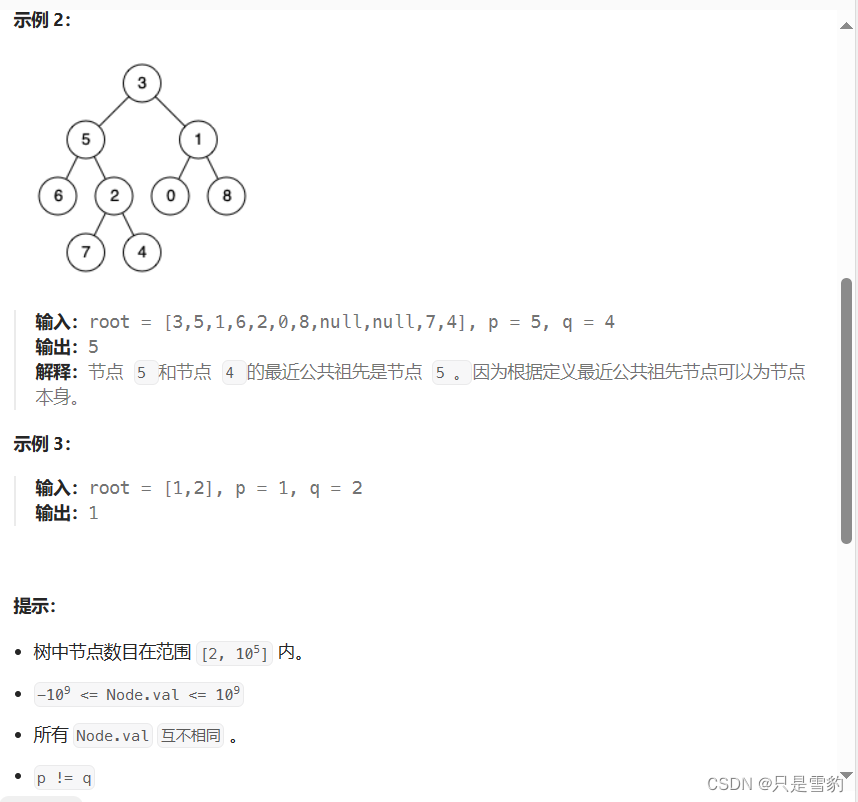
其实我们画图之后可以看到，公共祖先节点有几个很明显的特征：
如果一个节点在本节点的左子树，另一个在本节点的右子树上，那么这个节点就是那两个节点的公共祖先

如果两个节点都在一个节点的左或者右我们就用一个辅助函数来递归完成，都在左边或者右边那么两个节点之中有一个一定时他们两个节点的公共祖先

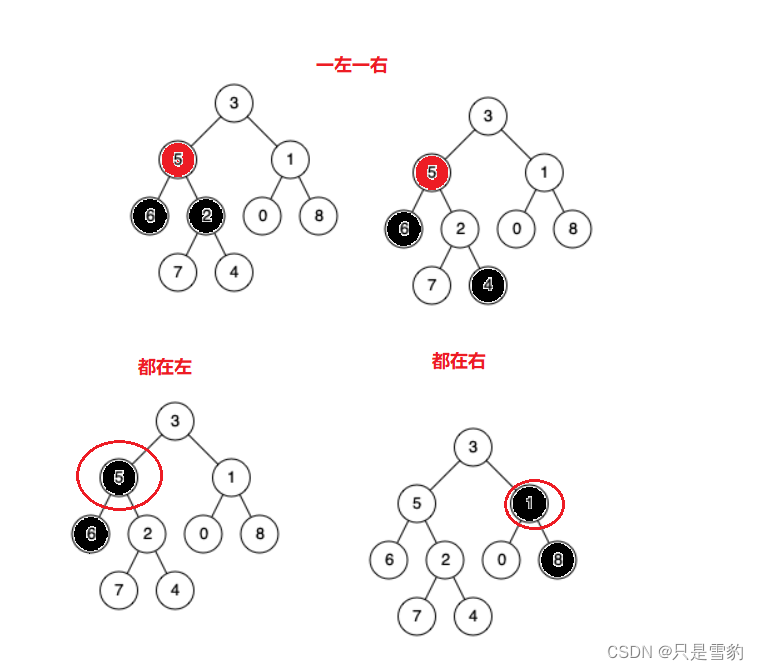
完整代码如下：

class Solution {
public:
//判断是否在这个树上
bool isintree(TreeNode* root,TreeNode* x)
{if(root==nullptr)return false;if(root==x)return true;return isintree(root->left,x)||isintree(root->right,x);
}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==p||root==q)return root;bool pinleft=isintree(root->left,p);bool pinright=isintree(root->right,p);bool qinleft=isintree(root->left,q);bool qinright=isintree(root->right,q);//一个在左一个在右if((pinleft&&qinright)||(pinright&&qinleft))return root;//都在左if(pinleft&&qinleft)return lowestCommonAncestor(root->left,p,q);//都在右if(pinright&&qinright)return lowestCommonAncestor(root->right,p,q);return nullptr;}
};

二叉树搜索树转换成排序双向链表

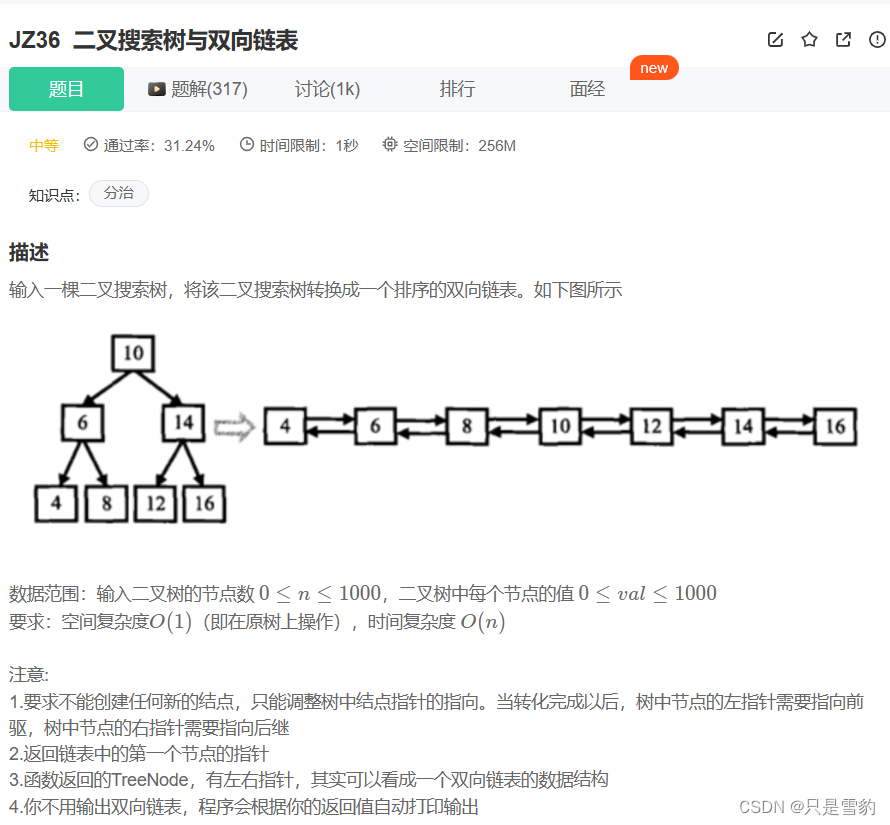
我们观察可以看到，最后排序出来的双向链表是一个有序的链表，而二叉搜索树的中序遍历一定是一个有序的序列，所以我们在这里要定义一个中序遍历的函数来用到解题

我们需要用到一个辅助的prev节点，令cur的left为prev，如果prev不为空就令prev的right为cur即可

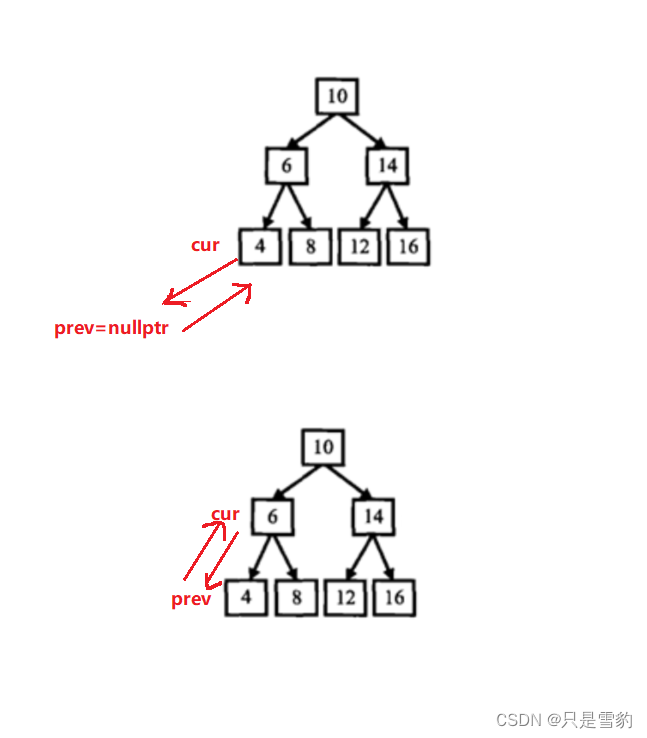
class Solution {
public:void inorder(TreeNode* cur,TreeNode*& prev){if(cur==nullptr)return;inorder(cur->left,prev);cur->left=prev;if(prev)prev->right=cur;prev=cur;inorder(cur->right,prev);}TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode* prev=nullptr;inorder(pRootOfTree,prev);TreeNode* head=pRootOfTree;while(head&&head->left){head=head->left;}return head;}
};

前序中序还原二叉树

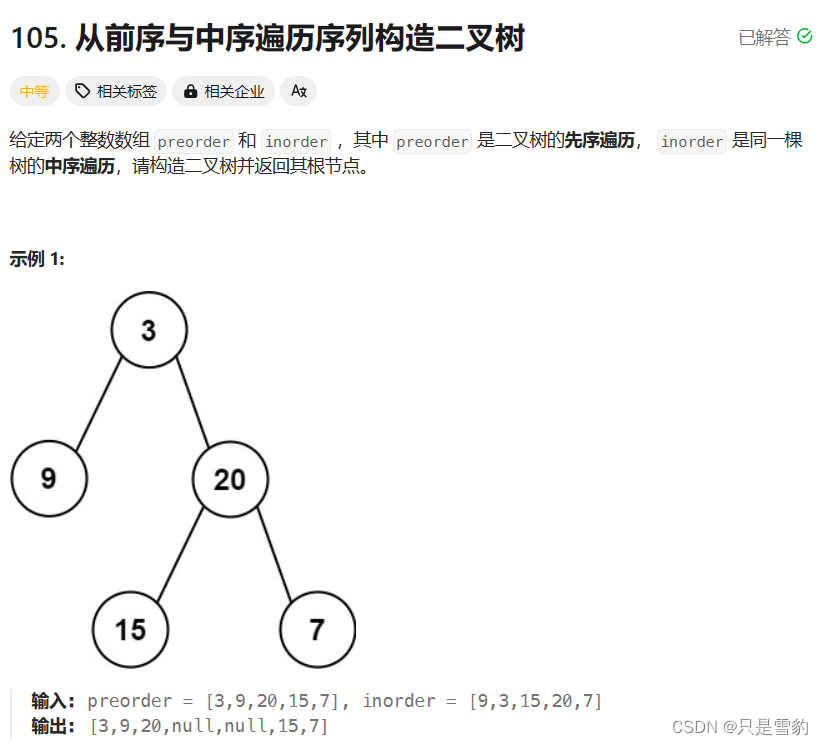
本题是根据前序和中序来构造二叉树，我们知道前序的第一个节点就是二叉树的根节点，而中序中根节点左边的就是左子树，右边为右子树，然后再遍历前序第二个节点，再次带入中序，前序的“根节点”能够将中序分为两个区间，分为区间后我们再递归两个区间

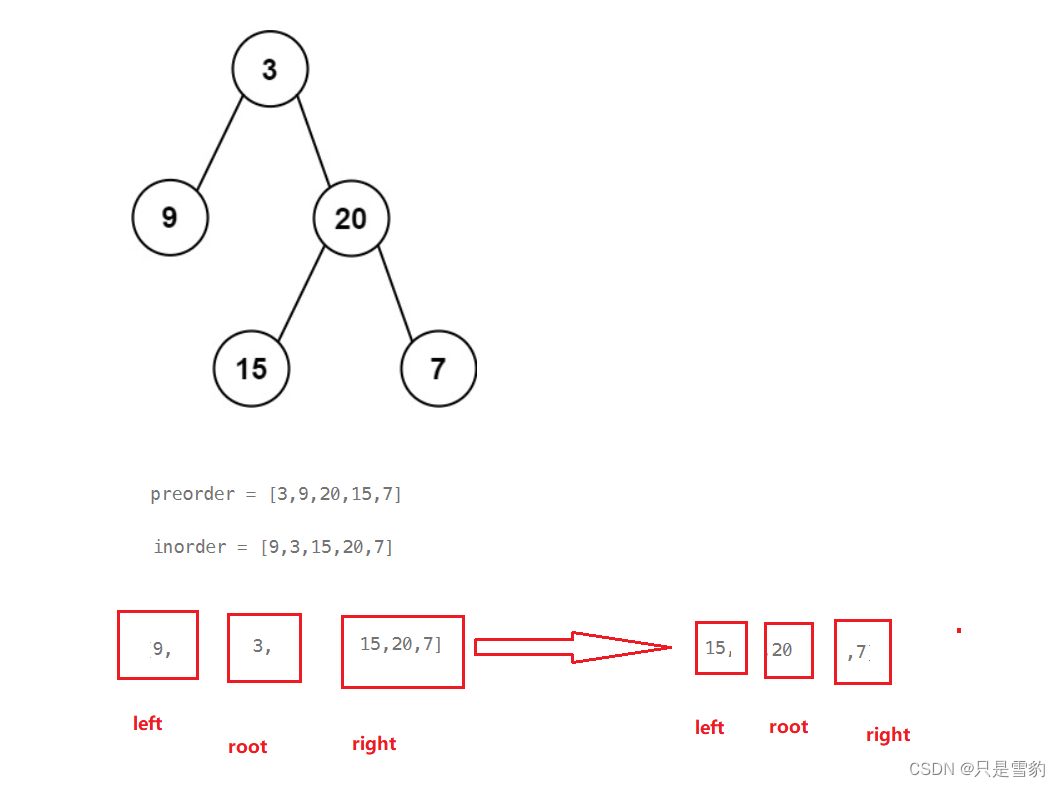
完整代码如下：

class Solution {
public:TreeNode* _buildTree(vector<int>& preorder,vector<int>& inorder,int& prei,int begin,int end){if(begin>end)return nullptr;TreeNode* root=new TreeNode(preorder[prei]);int rooti=begin;while(rooti<=end){if(inorder[rooti]==preorder[prei])break;elserooti++;}prei++;root->left=_buildTree(preorder,inorder,prei,begin,rooti-1);root->right=_buildTree(preorder,inorder,prei,rooti+1,end);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i=0;return _buildTree(preorder,inorder,i,0,inorder.size()-1);}
};

中序和后序还原二叉树

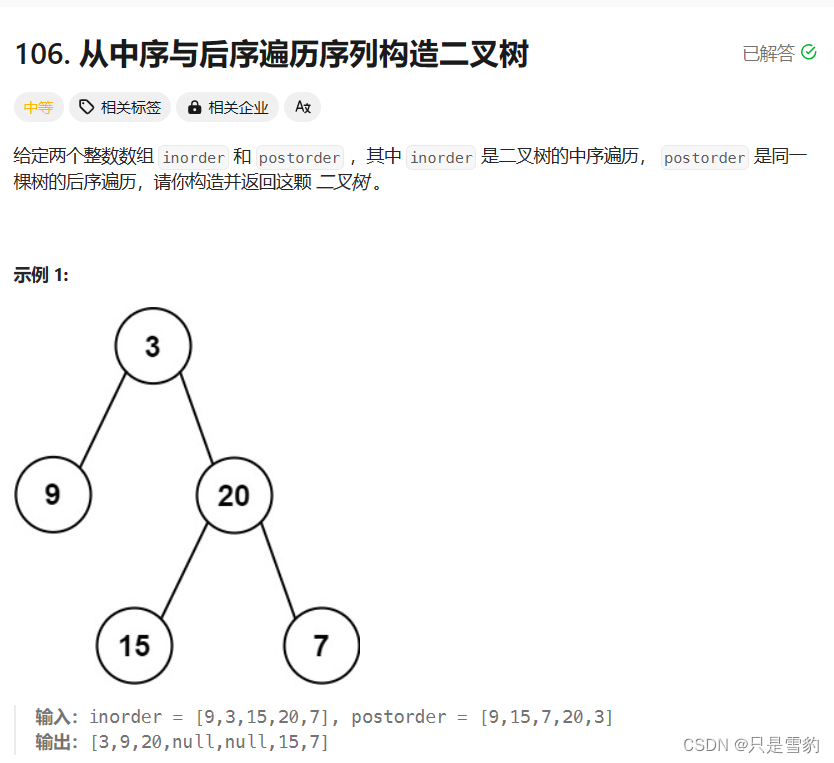
中序和后续构造二叉树就和前序和后续构造一样，转变一个思路：
但是要注意，由于后序是左右根，所以要先递归右在递归左

class Solution {
public:TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int& prei,int begin,int end){if(begin>end)return nullptr;TreeNode* root=new TreeNode(postorder[prei]);int rooti=begin;while(rooti<=end){if(inorder[rooti]==postorder[prei])break;elserooti++;}prei--;root->right=_buildTree(inorder,postorder,prei,rooti+1,end);root->left=_buildTree(inorder,postorder,prei,begin,rooti-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int i= postorder.size()-1;return _buildTree(inorder,postorder,i,0,inorder.size()-1);}
};