【LeetCode刷题】146. LRU 缓存-编程知识

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

思路：这道题的难点在于记录最近最少使用，使用map可以满足get的O(1)，但是无法记录最近最少使用的数据；如果使用数组，删除/增加的时间复杂度则是O(n)，也不满足。

使用哈希表 + 双向链表可以满足删除/增加的时间复杂度为O(1)。

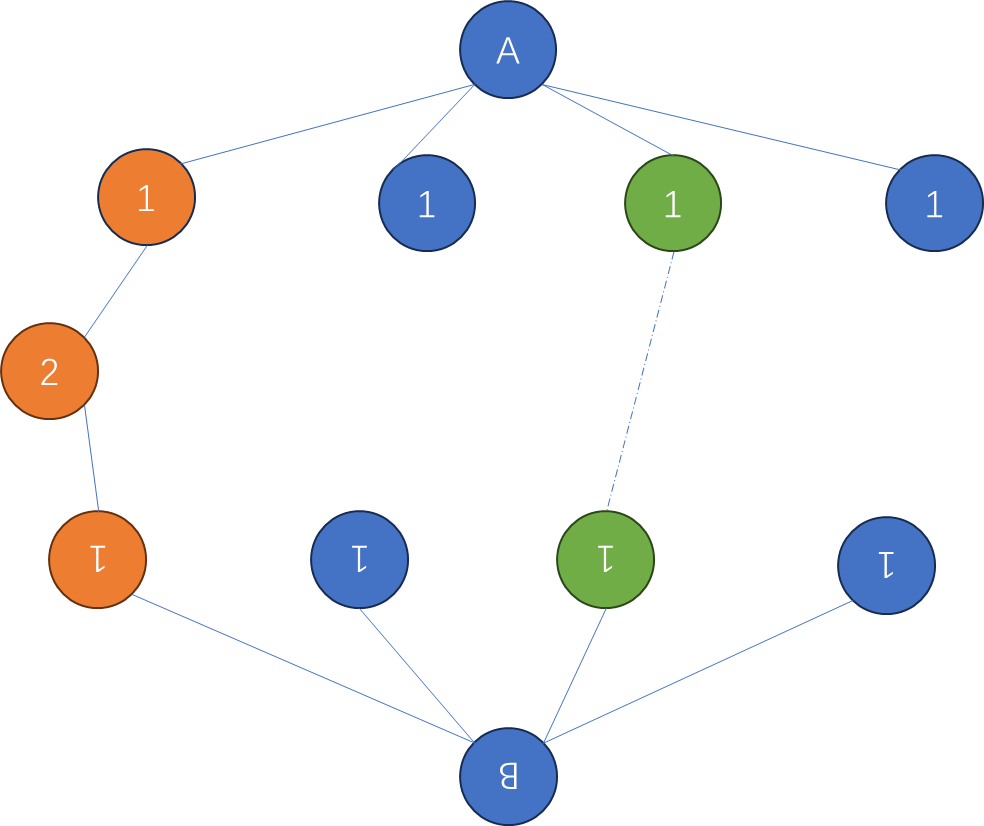
这个图太形象了。

（1）双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。

（2）哈希表即为普通的哈希映射（HashMap），通过缓存数据的键映射到其在双向链表中的位置。

（3）对于 get 操作，首先判断 key 是否存在：

（a）如果 key 不存在，则返回 −1；

（b）如果 key 存在，则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值。

（3）对于 put 操作，首先判断 key 是否存在：

（a）如果 key 不存在，使用 key 和 value 创建一个新的节点，在双向链表的头部添加该节点，并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量，如果超出容量，则删除双向链表的尾部节点，并删除哈希表中对应的项；

（b）如果 key 存在，则与 get 操作类似，先通过哈希表定位，再将对应的节点的值更新为 value，并将该节点移到双向链表的头部。

思路很清晰

class LRUCache {
public:LRUCache(int capacity) {}int get(int key) {}void put(int key, int value) {}
};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/

一步步实现：

（1）定义双链表

struct DLinkedNode {int key, value;             // k-vDLinkedNode* prev;          // 前向指针DLinkedNode* next;          // 后向指针// 两个构造函数DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};

（2）在LRUCache类中添加成员属性：哈希表+双向链表

class LRUCache {
public:// 新加的unordered_map<int, DLinkedNode*> cache;DLinkedNode* head;            // 伪头节点，不存数据DLinkedNode* tail;            // 伪尾节点，不存数据int size;                     // 当前存储的数量，当size==capacity时，要移出数据了int capacity;                 // 容量// 实现构造函数LRUCache(int _capacity): capacity(_capacity), size(0) {// 使用伪头节点和伪尾节点，不存数据head = new DLinkedNode();tail = new DLinkedNode();// 开始时一个数据都没有head->next = tail;tail->prev = head;}int get(int key) {}void put(int key, int value) {}
};

（3）实现双向链表中的【在头部添加数据】、【任意位置删除数据】、【数据移动到头部】、【从尾部删除数据】

在头部添加数据

    // 在头部添加数据void addToHead(DLinkedNode* node) {node->prev = head;node->next = head->next;head->next->prev = node;head->next = node;}

任意位置删除数据

    // 任意位置删除数据void removeNode(DLinkedNode* node) {node->prev->next = node->next;node->next->prev = node->prev;}

数据移动到头部

    // 移动数据到头部void moveToHead(DLinkedNode* node) {removeNode(node);addToHead(node);}

从尾部删除数据

    // 从尾部删除数据DLinkedNode* reoveTail() {DLinkedNode* node = tail->prev;removeNode(node);return node;}

（4）实现get函数

如果不存在直接返回-1，存在的话，先通过哈希表定位，再移动到头部

    int get(int key) {// 不存在if (cache.count(key) == 0) {return -1;}// 通过哈希找到，移动到头部DLinkedNode* node = cache[key];moveToHead(node);return node->value;}

（5）实现put函数

如果key不存在，则创建一个节点，注意size==capacity的情况，此时删除队尾数据

靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。

如果存在，修改value，再将该节点移动到队头

 void put(int key, int value) {// 不存在if (cache.count(key) == 0) {DLinkedNode* node = new DLinkedNode(key, value);cache[key] = node;          // 添加到哈希表中addToHead(node);            // 移动到队头size++;if (size > capacity) {DLinkedNode* removeNode = reoveTail();  // 删除尾部数据cache.erase(removeNode->key);           // 删除哈希中的数据delete removeNode;size--; }} else {DLinkedNode* node = cache[key];node->value = value;moveToHead(node);               // 移到队头}}

全部代码实现

struct DLinkedNode {int key, value;             // k-vDLinkedNode* prev;          // 前向指针DLinkedNode* next;          // 后向指针// 两个构造函数DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};class LRUCache {
public:unordered_map<int, DLinkedNode*> cache;DLinkedNode* head;DLinkedNode* tail;int size;int capacity;LRUCache(int _capacity): capacity(_capacity), size(0) {// 使用伪头节点和伪伪节点，不存数据head = new DLinkedNode();tail = new DLinkedNode();// 开始时一个数据都没有head->next = tail;tail->prev = head;}int get(int key) {// 不存在if (cache.count(key) == 0) {return -1;}// 通过哈希找到，移动到头部DLinkedNode* node = cache[key];moveToHead(node);return node->value;}void put(int key, int value) {// 不存在if (cache.count(key) == 0) {DLinkedNode* node = new DLinkedNode(key, value);cache[key] = node;          // 添加到哈希表中addToHead(node);            // 移动到队头size++;if (size > capacity) {DLinkedNode* removeNode = reoveTail();  // 删除尾部数据cache.erase(removeNode->key);           // 删除哈希中的数据delete removeNode;size--; }} else {DLinkedNode* node = cache[key];node->value = value;moveToHead(node);               // 移到队头}}// 在头部添加数据void addToHead(DLinkedNode* node) {node->prev = head;node->next = head->next;head->next->prev = node;head->next = node;}// 任意位置删除数据void removeNode(DLinkedNode* node) {node->prev->next = node->next;node->next->prev = node->prev;}// 移动数据到头部void moveToHead(DLinkedNode* node) {removeNode(node);addToHead(node);}// 从尾部删除数据DLinkedNode* reoveTail() {DLinkedNode* node = tail->prev;removeNode(node);return node;}};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/

参考：【字节一面】 LRU Cache 实现剖析_哔哩哔哩_bilibili

链接：. - 力扣（LeetCode）