如果有这么一个线性规划系统的例子:
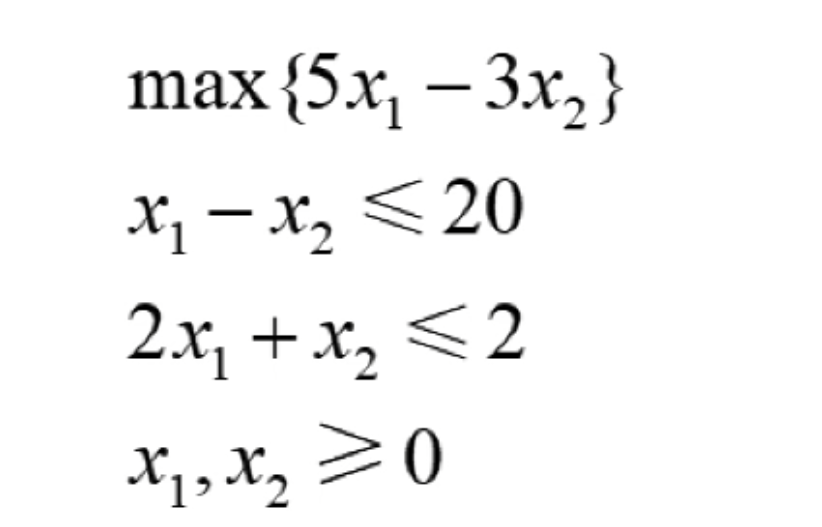
添加图片注释,不超过 140 字(可选)
将如上的线性规划系统转换为:
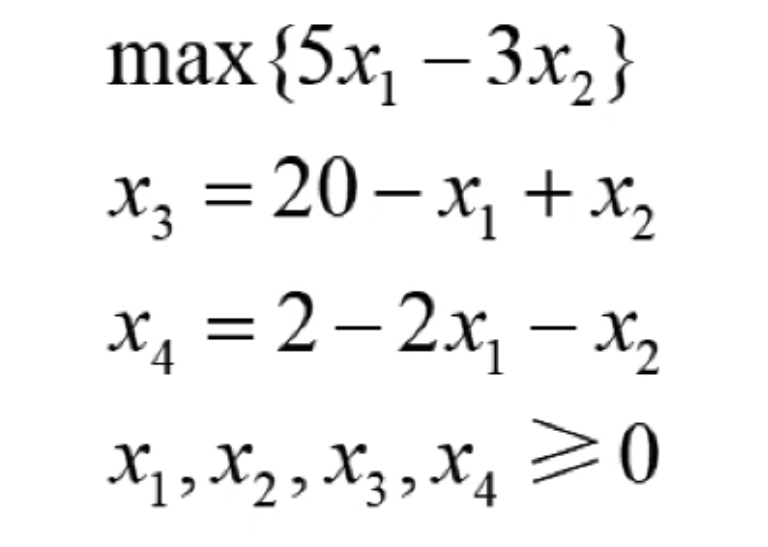
添加图片注释,不超过 140 字(可选)
这里要注意的是转换后的约束条件全部都变成了等号的约束,它与前面用的高斯消元法的方程组很相似,约束条件所形成的方程组有4个变量,但是只有两个方程,因此这个方程组有无限的解,这里只关注一些具有特定性质的解。
一些特定的解,就是把约束条件等号右边变量全部设置为0,然后得到等号左边变量的值,这种解也就是基本解,例如,将x1和x2设置为0,然后就得到了x3=20,x4=2,因此得到的一组基本解。
根据这组基本解,就有了目标函数的值是0,接下来要在这组基本解上反复的迭代变换,直到最后得到让目标条件最大化的解,从目标函数中找到一个系数为正数的变量,例如当前目标函数中的x1的系数是5,选中这个变量。
然后再不破坏约束条件的情况下,尽可能增加它的值,在x1增加时有可能会导致其他变量减少,但在约束条件中要求所有变量都必须要大于0,因此x1不能无限制的增加,从第一个约束条件可以看出,当x1增加超过20的时候变量x3就会变得小于0了,根据第二个约束条件可以看出,当x1增加超过1的时候,x4就会变得小于0了,由此可以确定x1的增加不能超过1。
由于第二个约束条件对应x1的增加量最少,所以要从第二个约束条件入手将x1反解出来变成如下的式子:

添加图片注释,不超过 140 字(可选)
然后将式子带入其他右边包含变量x1的约束条件中
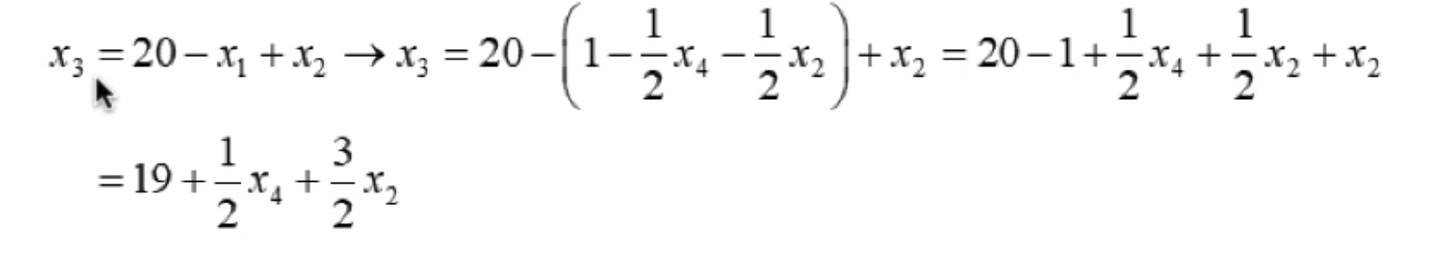
添加图片注释,不超过 140 字(可选)
同时也把目标函数中的变量x1也替换掉,得到的结果如下:
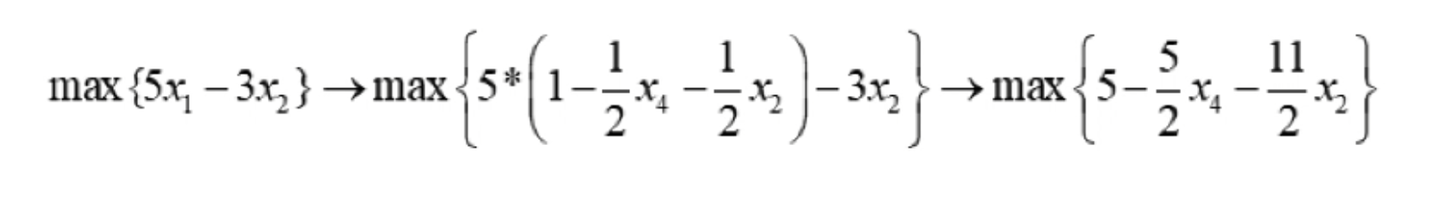
添加图片注释,不超过 140 字(可选)
于是原来的线性规划系统也就变成了:
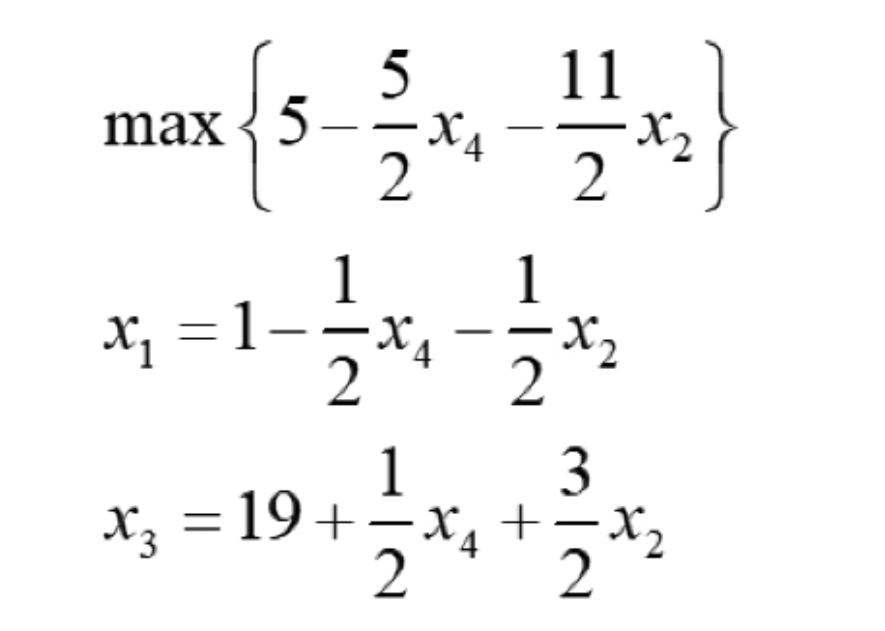
添加图片注释,不超过 140 字(可选)
这一个变换的过程也就叫做pivot变换,这个与变换前的线性规划系统对应目标函数带入基本解后的结果是一样的。

![[Vulnhub]靶场 Red](https://img-blog.csdnimg.cn/direct/908c0ef3ca7a40c38b753475fd84516d.png)