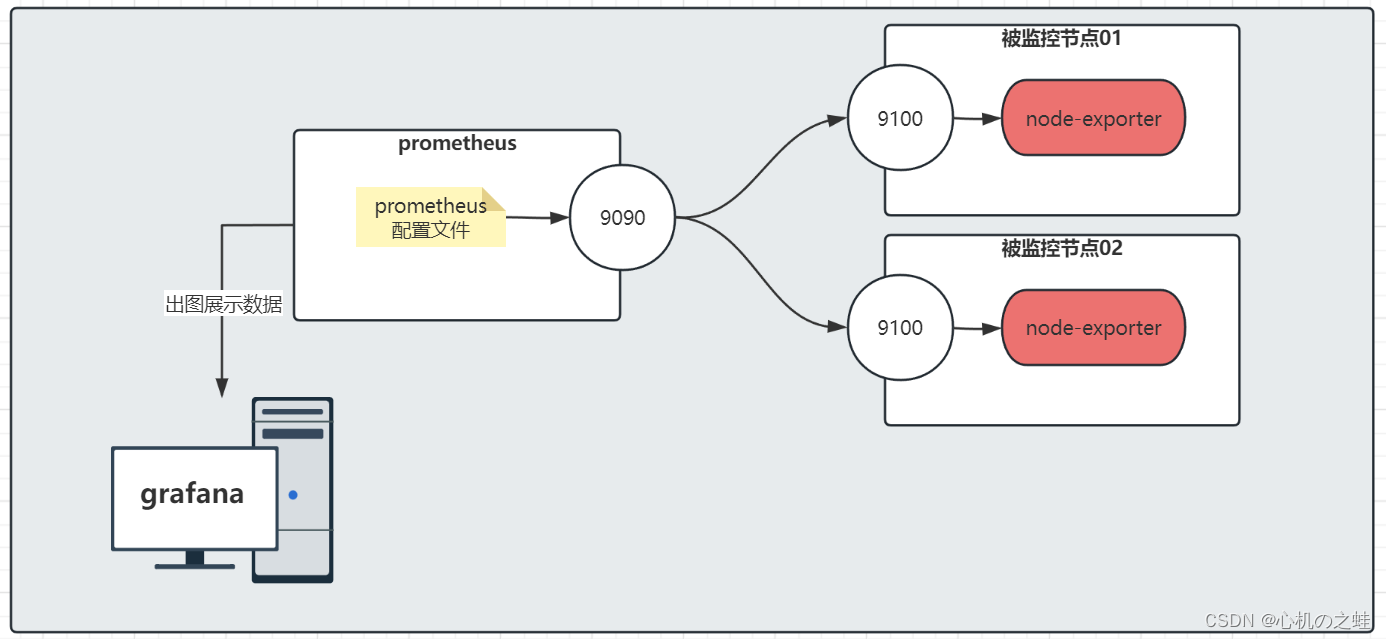
一、准备环境
为了实现下拉列表筛选的样例,我们监控两个linux节点;
目前,我们已经有了一个节点了,再添加一个;
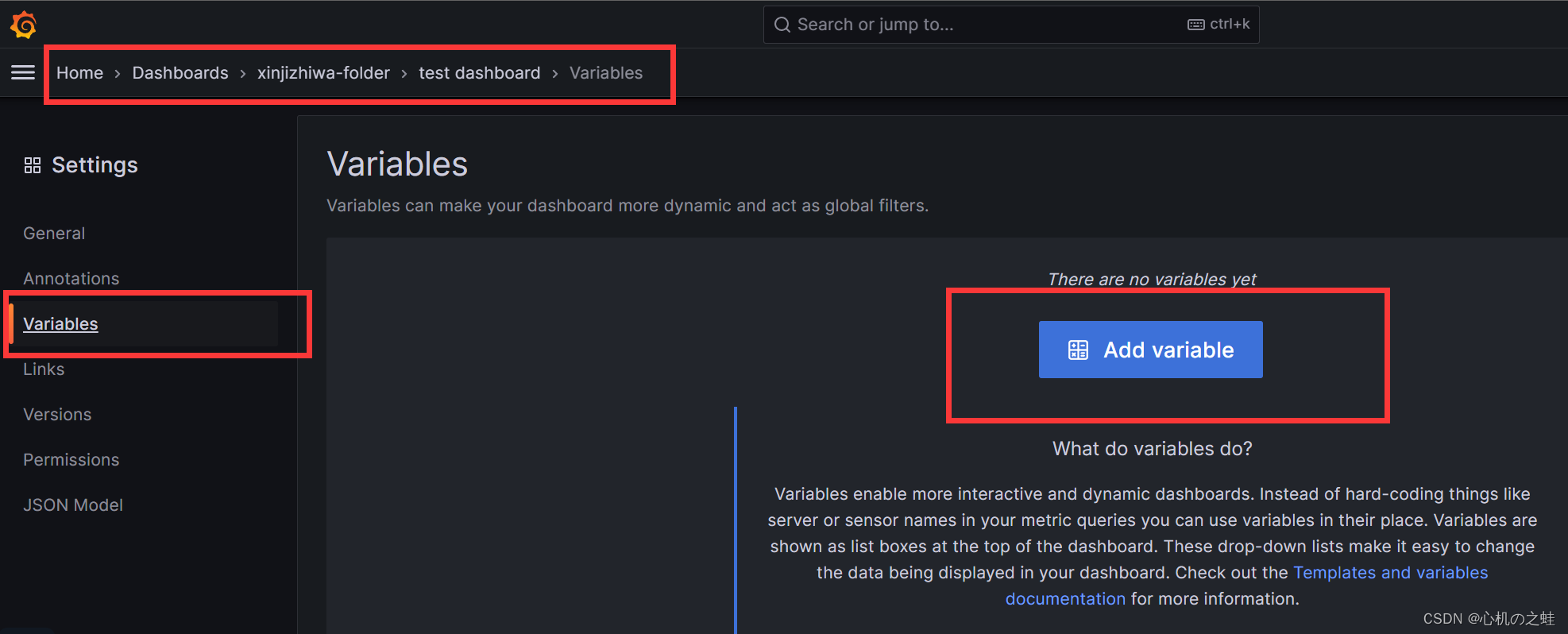
二、grafana的仪表盘变量
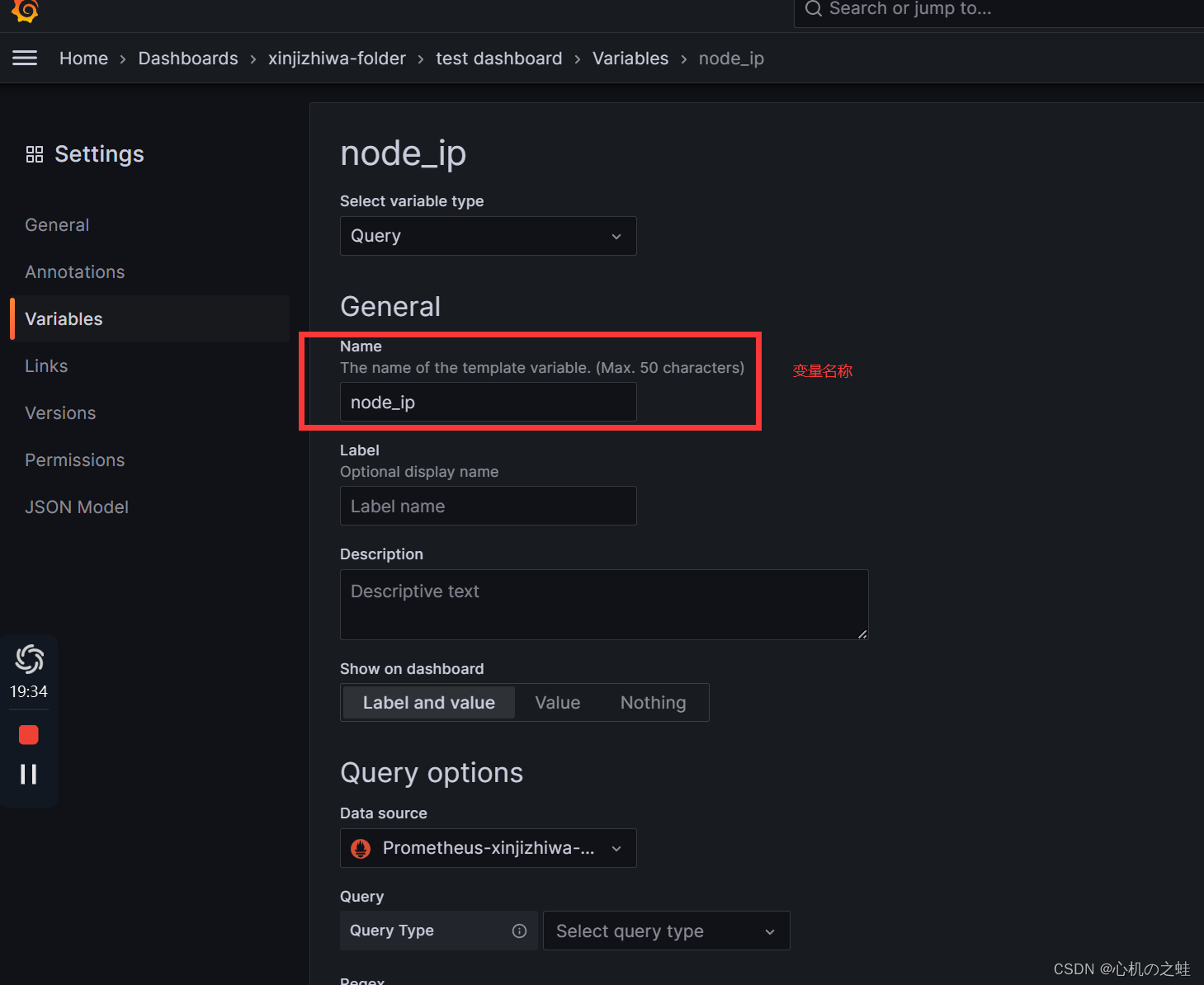
如果想给仪表盘自定义下拉列表,那么,需要设置变量,变量的位置如下图:
注意:是给仪表盘设置变量;
1,变量的名称
只能写数字、字母和“_”,其他的字符不还使;
变量名,就是引用的时候使用的。
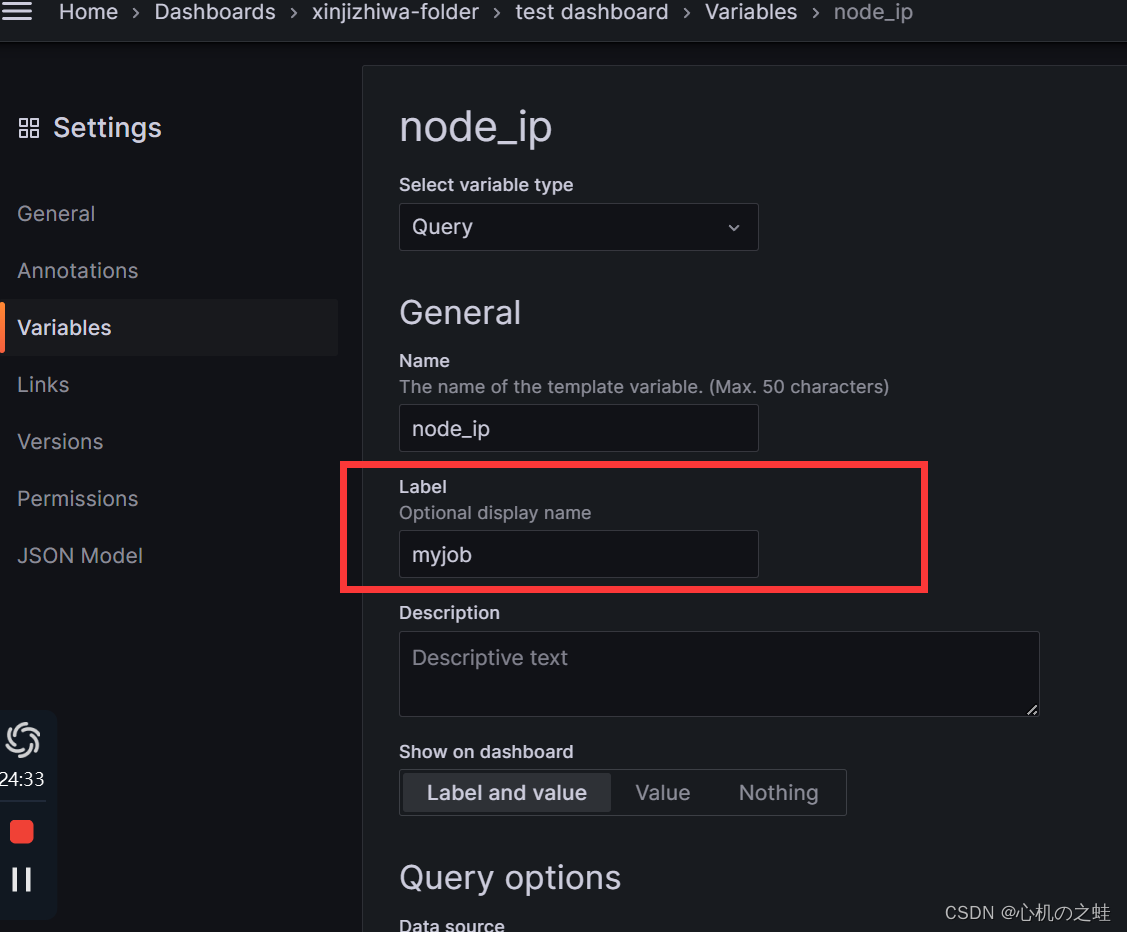
2,可选选项的名称
就是仪表盘下拉列表前面的指示字段
案例释义:
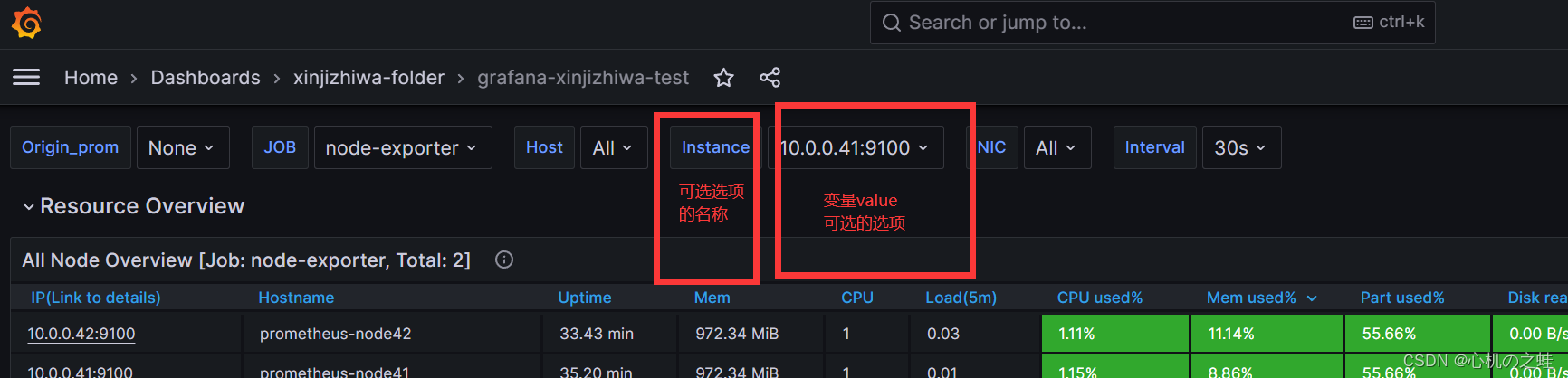
3,选择数据源和数据标量的key
实际意义就是,将数据源中的哪个key,当做下拉列表的字段;
操作那个数据作为变量?

job有很多个(我们目前是两个),选择哪个job?
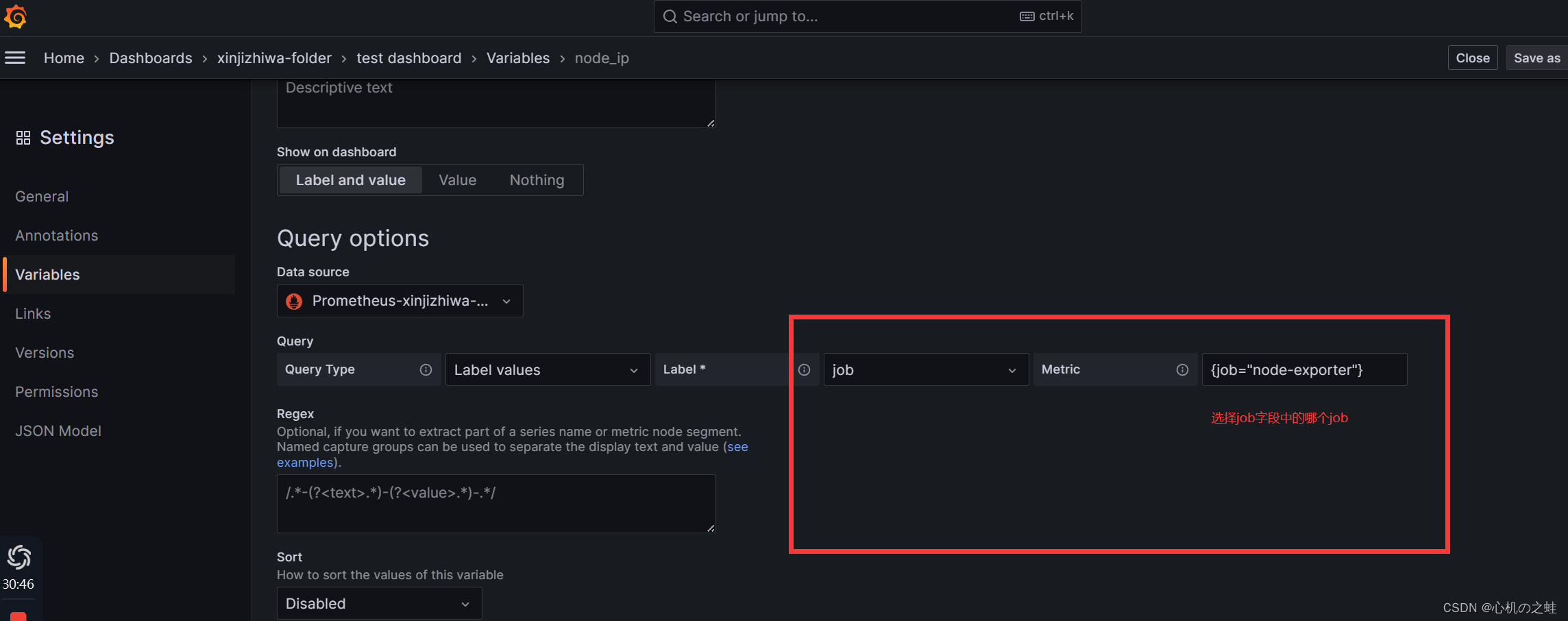
会自动显示出我们的编辑结果
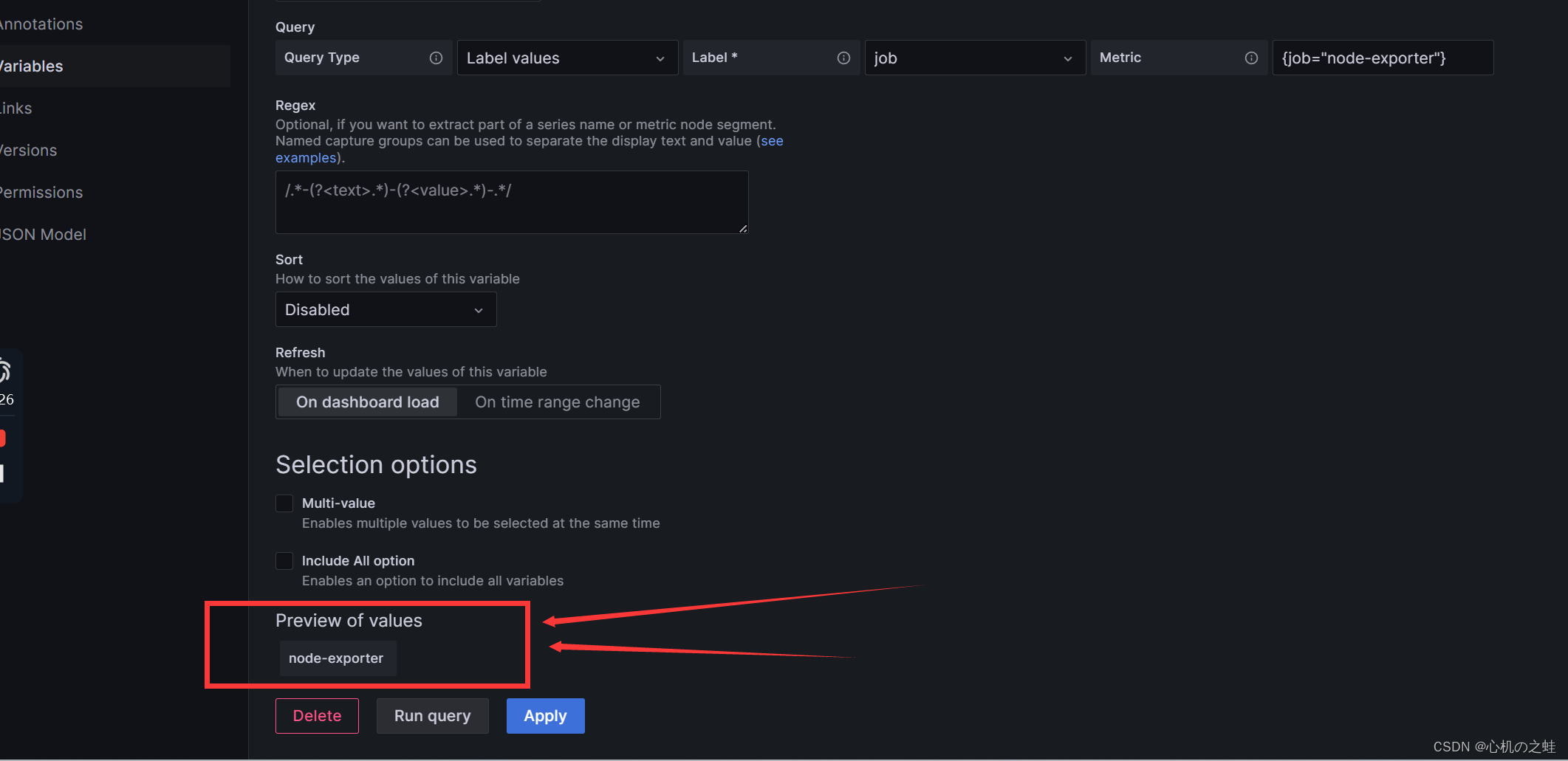
只要保存,我们的自定义的仪表盘就出现了这个变量的下拉列表;
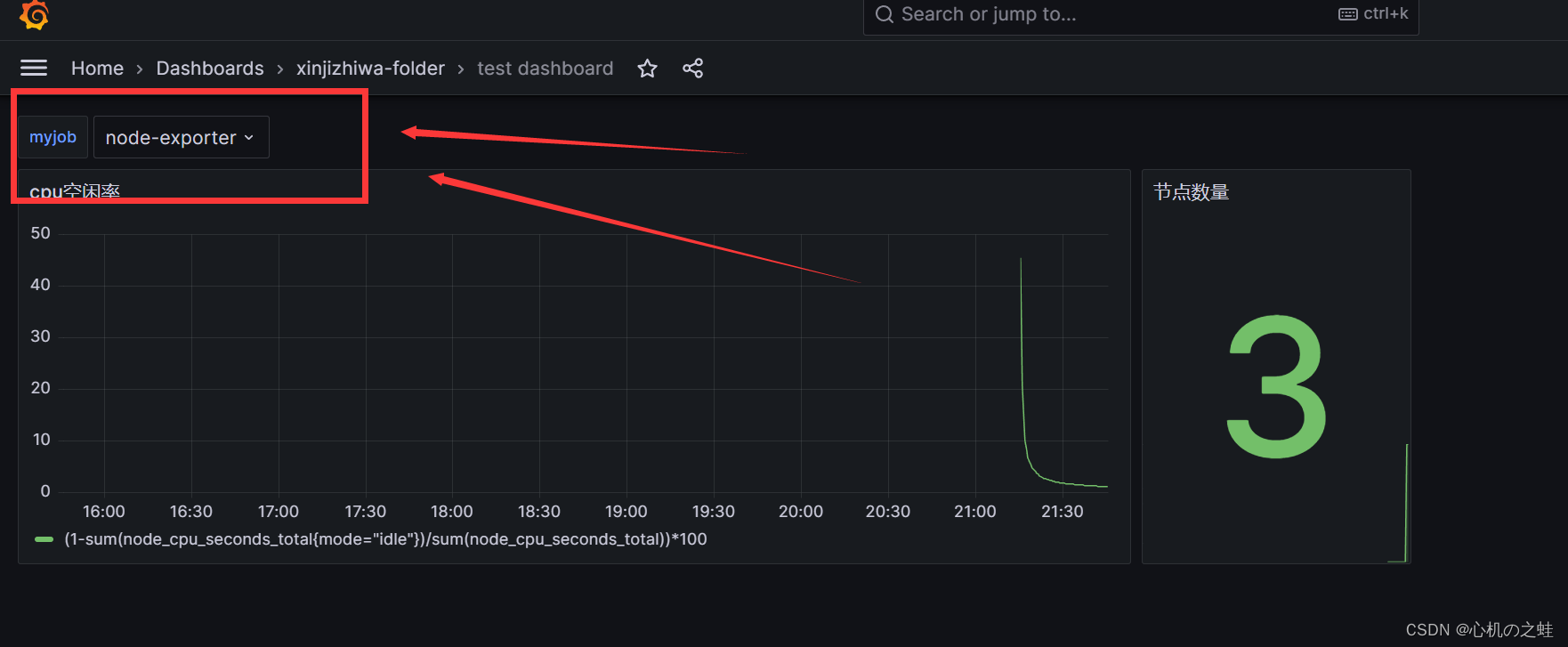
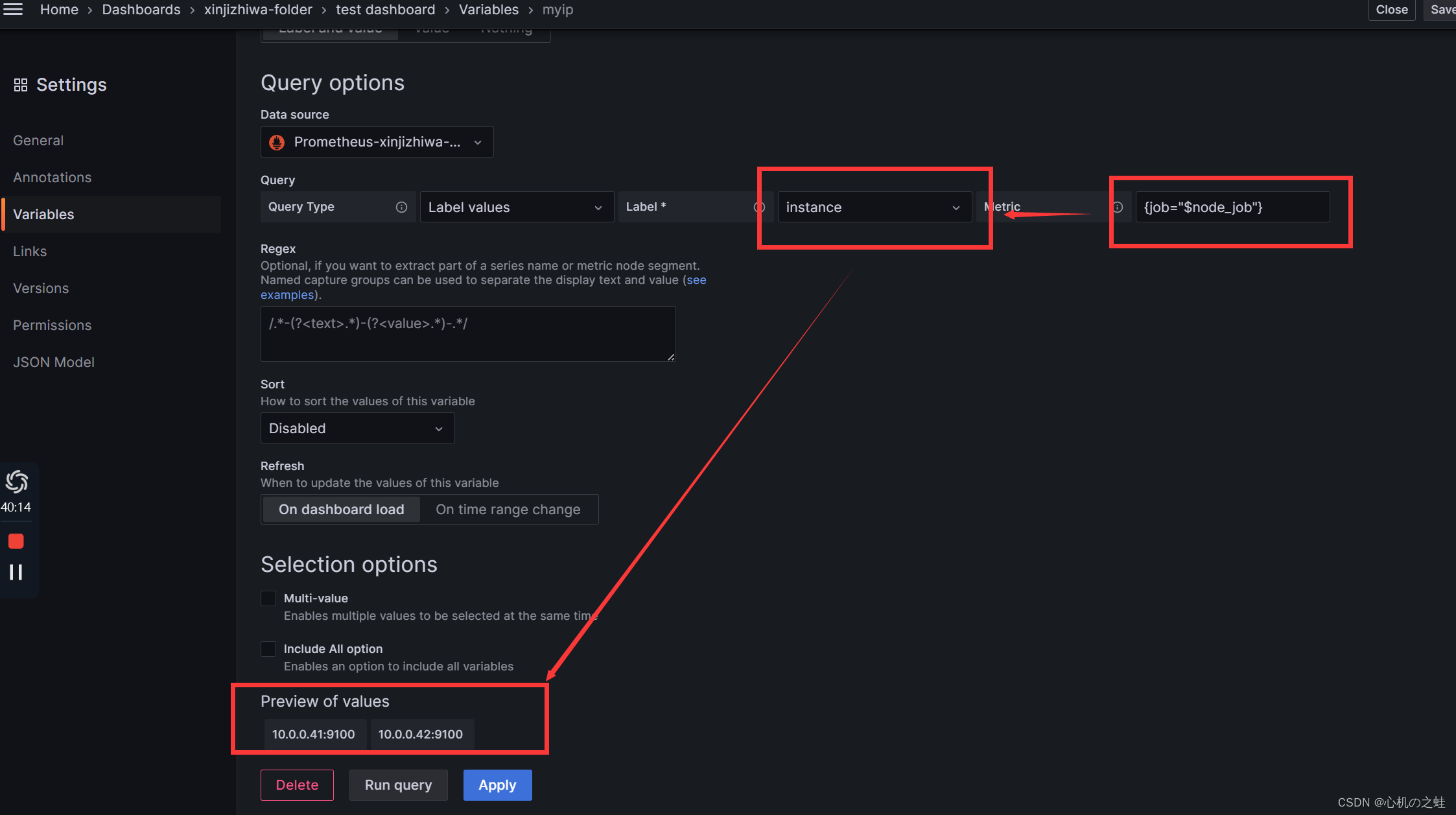
三、给变量设置变量
我们现在有了,job列表的选项,现在再添加一个ip列表的选项;
从myjob的变量中获取instance列表信息;
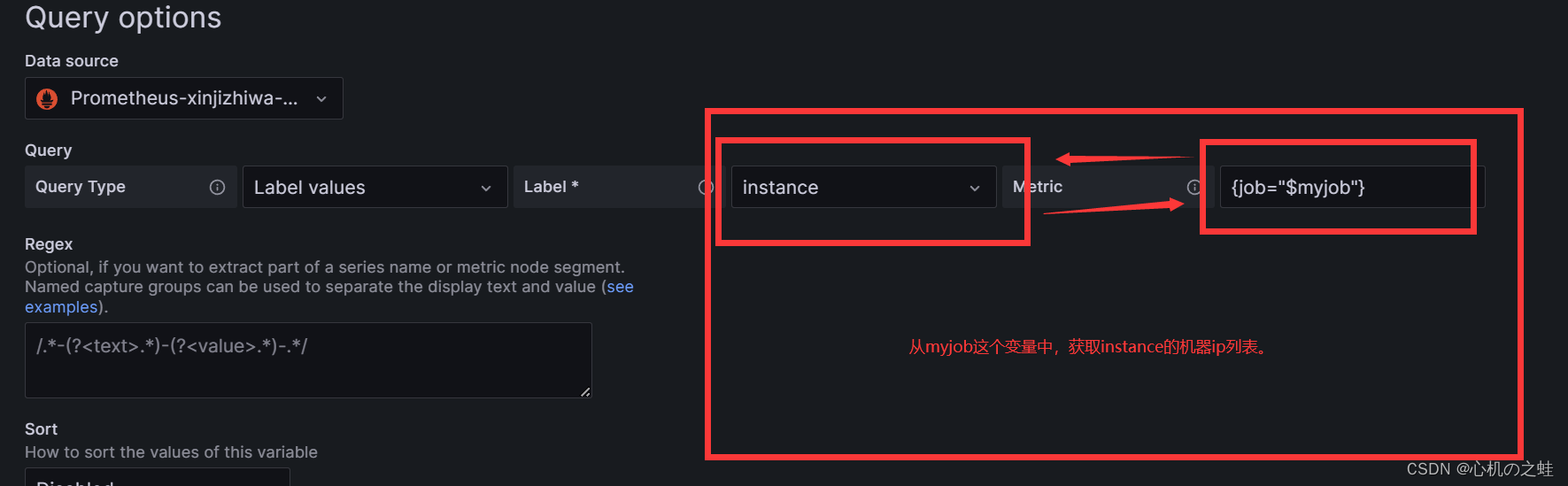
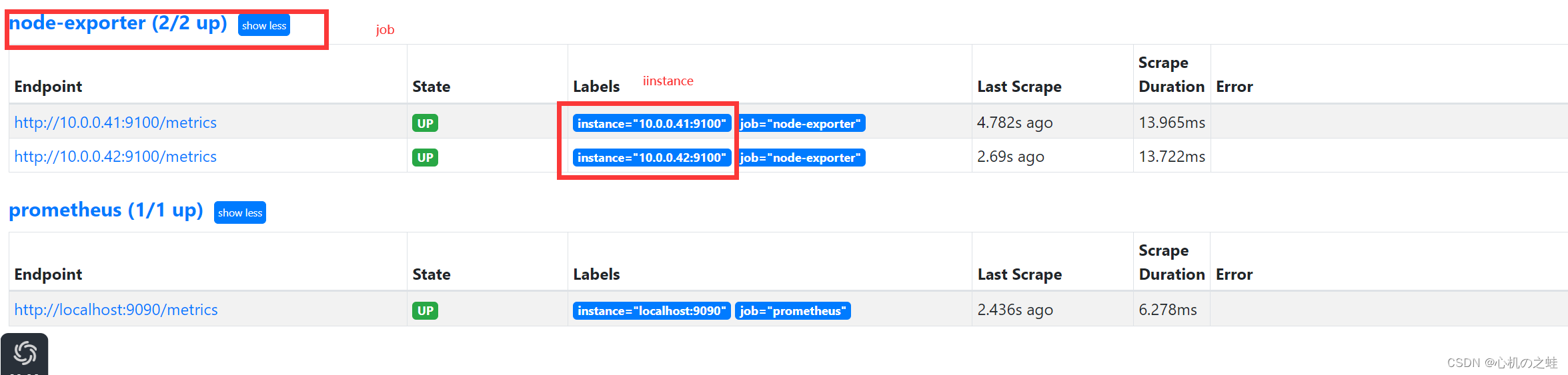
apply保存变量,回到仪表盘;就可以看见二级列表了;
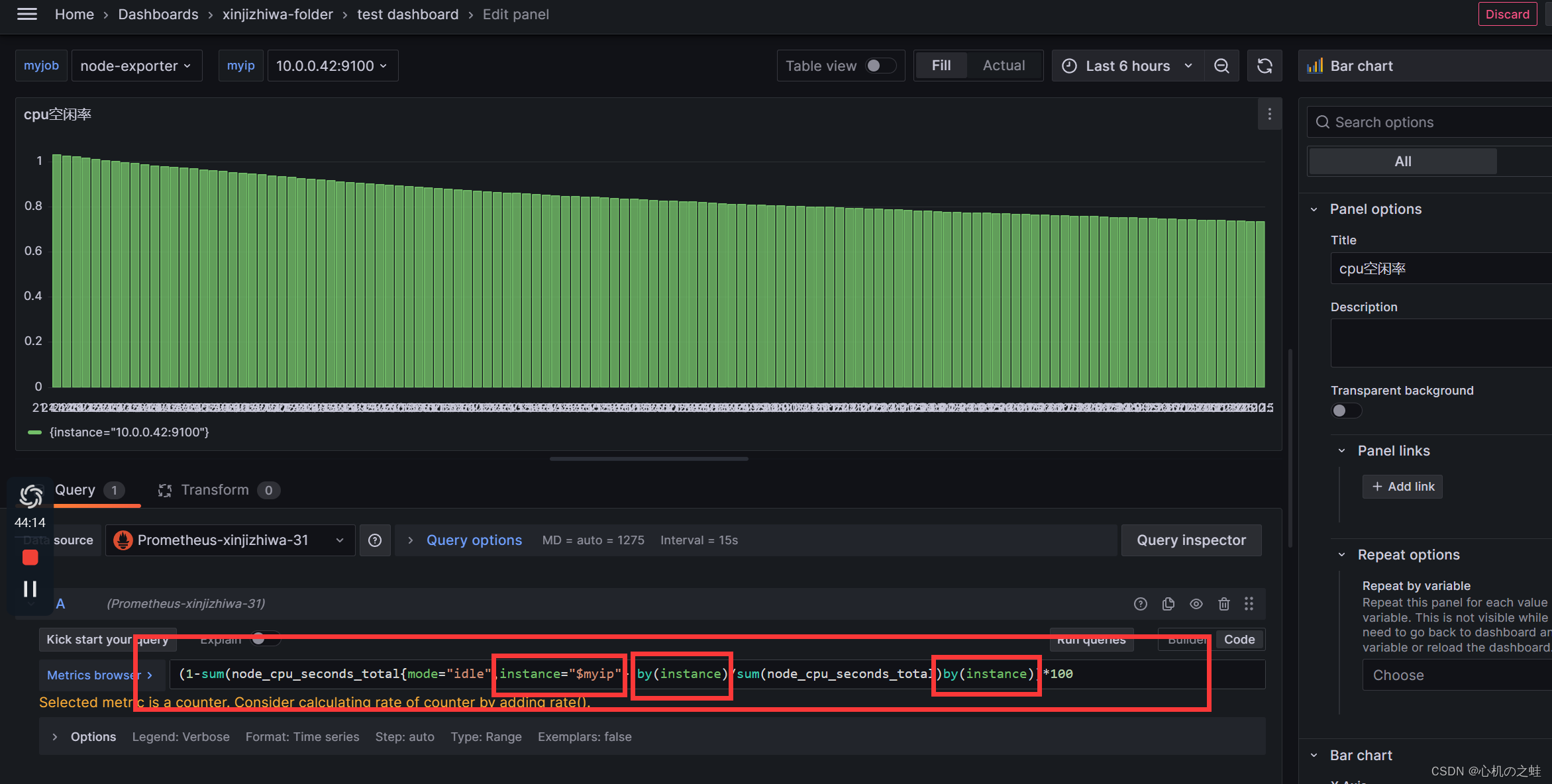
四、仪表盘模块代码引用变量
筛选数据的时候,引用变量筛选,再通过变量的结果进行分组,得到切换列表就切换数据的效果。
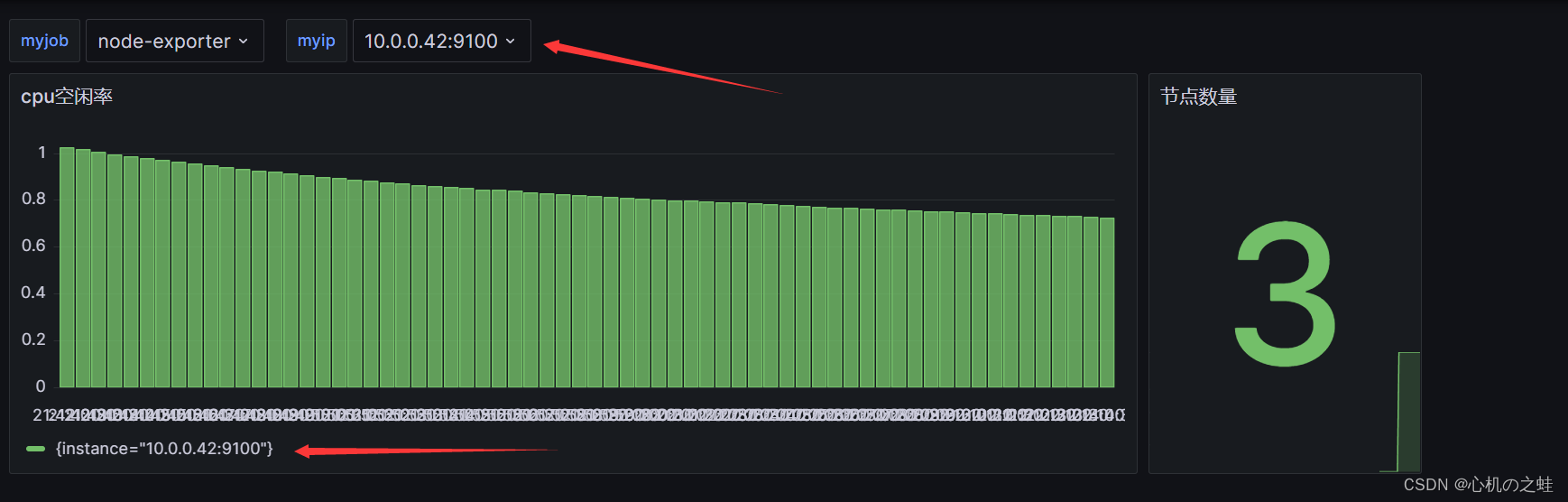
演示结果
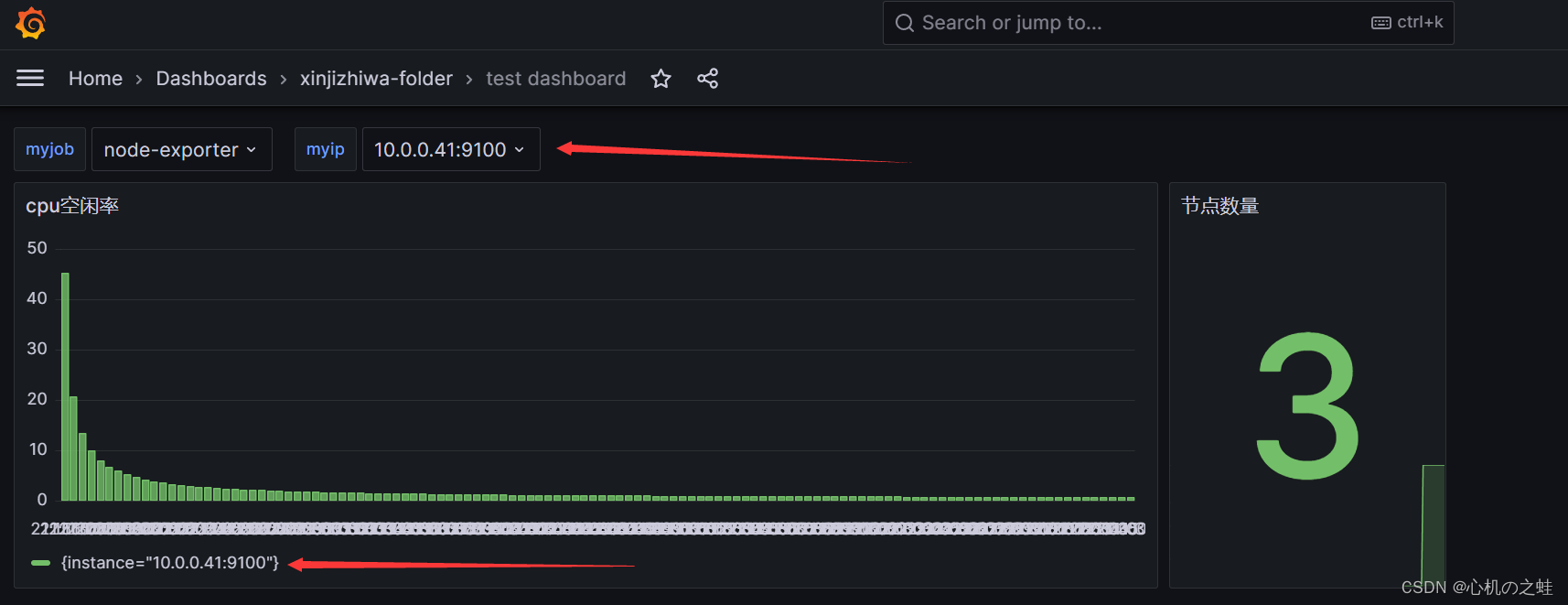
至此,grafana的变量,就学到这里,不会的群里反馈,或者评论区弹幕说出来,我随时会看,并在群中给大家详细讲解。