数字化时代,个人身份已不再仅仅局限于传统形式,分布式数字身份(Decentralized Identity,简称DID)正崭露头角,它允许个人通过数字签名等加密技术,完全掌握和控制自己的身份信息。研究报告显示,预计到2027年,全球分布式数字身份市场规模将达到68亿美元,年复合增长率高达88.7%。
在这篇文章里,我们将对DID作为个人身份标识符在连接Web2.0与Web3.0方面的应用进行探讨。
01
通往Web3.0的钥匙
以BSN的理念来看,我们正走向一个单方系统与基于分布式技术的多方系统并存的未来,也就是近两年来科技行业经常谈论的Web2.0与Web3.0。Web3.0不会取代Web2.0,而是在某些方面解决了效率问题,并开辟了新的应用场景。
在这一过程中,DID将在重新塑造人们与数字生态系统互动的方式上发挥关键作用,DID能够将人们与众多分布式应用连接起来。依托于区块链技术的固有特性:不可篡改性、去中心化和透明性,DID相较于传统的数字身份在以下几个方面具有显著的优势:
第一、自主身份:个人可以完全拥有和控制自己的数字身份;
第二、数据安全:不存在第三方持有或管理用户数据,避免了个人数据泄露或遭滥用的风险;
第三、互操作性:在当下高度碎片化的网络环境中,用户的数据被分割存储在各个业务平台数据库中。DID提供了一种安全的技术手段,通过授权签名将这些离散的数据关联起来,在保障用户隐私安全的前提下实现数据互操作。这不仅为商业模式的创新提供了重要基石,也使得基于多源异构数据的分布式决策和协作成为可能。
作为通往Web3.0世界的钥匙,分布式数字身份正在改变人们在数字世界的互动方式。依托区块链的技术优势,它赋予个人前所未有的数字身份控制权,并支持跨平台的身份关联与数据互操作。正因如此,在Web3.0时代实现碎片化数据的有效聚合整合与多方安全协作将成为分布式数字身份技术的重要应用之一。
02
重塑数字身份体系
在Web3.0中,DID将取代人们熟知的“用户名+密码”这种数字身份体系。用户不再需要设置和记忆多个账号和密码,而是可以通过DID和数字签名,选择性地将自己的身份与各类应用关联起来,无论是实名还是匿名场景。
这种变革大大简化了用户体验,用户不再需要重复注册账号、设置密码,也无需担心遗忘密码的尴尬。更为重要的是安全性得到了极大提升。在Web2.0时代,用户身份数据高度集中存储在业务平台数据库中,数据库被黑客攻击导致大规模信息失窃等情况屡见不鲜,这使得用户面临巨大的隐私泄露风险以及身份盗用风险,
而DID彻底颠覆了这一体系。基于加密算法的签名验证取代了密码验证,用户的敏感身份数据也不再集中存储,这样就消除了巨大的中心化数据库泄密风险。
不仅如此,DID还赋予了用户前所未有的数字身份自主控制能力。首先,用户可以选择性披露信息,不同验证方只能获取到用户主动授权的最小化数据;其次,即使选择披露,用户也可以随时收回数据访问权限;最后,在整个数据交互过程用户可以始终保持匿名,避免隐私泄漏。
通过以上技术手段,DID极大增强了用户对自身数字身份和个人敏感数据的控制力。在个人信息保护意识日益增强的今天,这种安全可靠的数字身份管理模式显得尤为重要,它将引领用户数据新一轮的安全升级革新。
03
BSN实名DID服务
2023年底,BSN正式推出了“BSN实名DID服务”,作为区块链产业和数字身份产业的创新融合,BSN实名DID服务充分融合了BSN区块链服务网络和CTID数字身份链两大基础设施,有效拓展了我国身份认证体系,能够更好地为Web3.0时代多方协作的分布式应用场景服务。
作为一项底层技术,BSN实名DID服务可以助力业务接入机构构建多元化的数字身份服务体系,打造覆盖个人数据实名确权、个人隐私保护登录、数据加密流转等各种场景的解决方案,有效保障个人隐私数据安全。
可以说,BSN实名DID服务正通过技术和应用双轮驱动,助力我国数字身份体系向纵深发展。它与传统身份体系的有机衔接,也将共同奠定Web3.0中新兴数字身份基础设施的发展方向,对整个互联网和IT系统的发展产生深远影响。
相信在不远的将来,随着数字化进程的不断深入,BSN实名DID服务将逐步拓展至所有需要进行实名认证的业务场景,创造出巨大的价值。也欢迎所有对BSN实名DID服务感兴趣的业务平台,与我们一起开拓更多的应用场景。
分布式数字身份:通往Web3.0世界的个人钥匙
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/513703.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
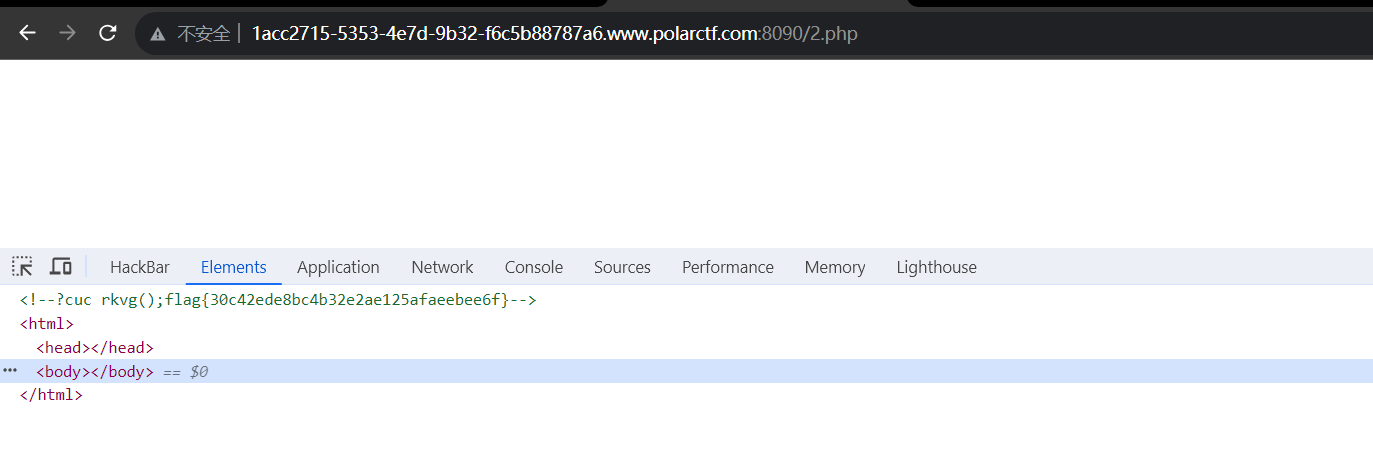
Polar 写shell
Polar 写shell
直接给了源码 还是没啥好说的,考点是die()死亡函数绕过之不同变量 **绕过原理: **通过base64解密或rot13解密使"<?php exit();"变为乱码,而传入的$content为base64编码,解码后为正常shell语句。通过…
智慧城市中的数字孪生:构建城市管理的未来框架
目录
一、引言
二、数字孪生技术概述
三、数字孪生技术在智慧城市中的应用
1、实时监测与预警
2、模拟与优化
3、智能化决策
4、协同与共享
四、数字孪生技术构建城市管理的未来框架的价值
1、提高管理效率
2、优化资源配置
3、提升公共服务水平
4、增强应对突发事…
K8s集群调度,亲和性,污点,容忍,排障
目录
1.调度约束
调度过程
指定调度节点
查看详细事件
获取标签帮助
修改成 nodeSelector 调度方式
2.亲和性
节点亲和性
Pod 亲和性
键值运算关系
硬策略
软策略
Pod亲和性与反亲和性
创建一个标签为 appmyapp01 的 Pod
使用 Pod 亲和性调度,创建多…
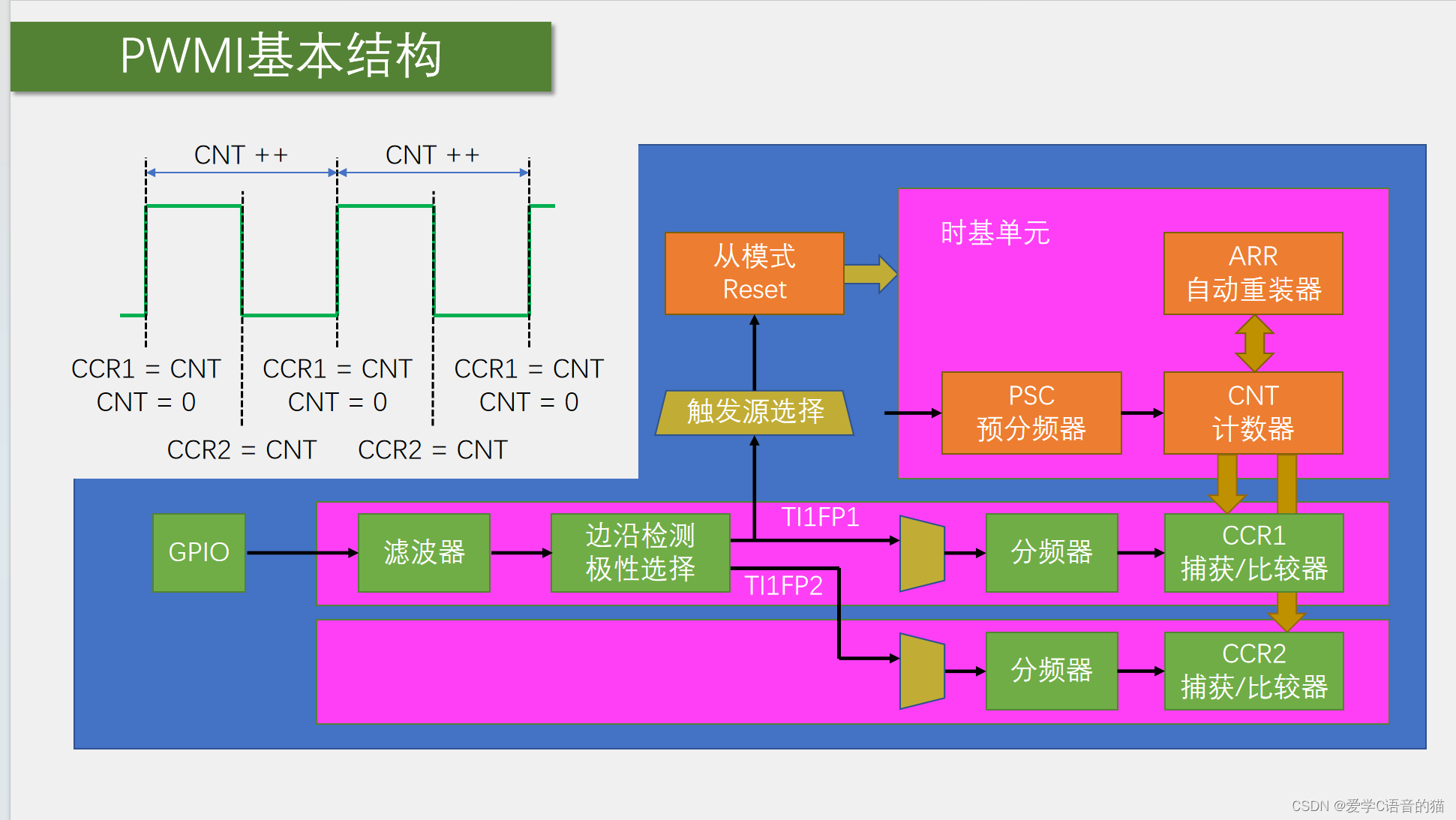
32单片机基础:TIM输入捕获
指定的电平跳变,就是上升沿或者下降沿,可以通过程序设置
PWMI模式,就是PWM的输入模式,是专门为测量PWM频率和占空比设计的,
可配合主从触发模式
这两个功能结合起来,测量频率占空比就是硬件全自动运行的…
分类算法入门:以鸢尾花数据集为例
近两年人工智能技术蓬勃发展,OpenAI连续放出ChatGPT、Sora等“王炸”产品,大模型、AIGC等技术带来了革命性的提升,很多人认为人工智能将引领第四次工业革命。国内各大互联网公司也是重点投资布局,从个人角度来说要尽快跟上时代的潮…
MyBatis操作数据库(SQL注入)
本文主要来讲解6大标签,以便更好的MyBatis操作数据库! <if>标签<trim>标签<where>标签<set>标签<foreach>标签<include>标签 前提需求:
MyBatis是一个持久层框架,和Spring没有任何关系&…
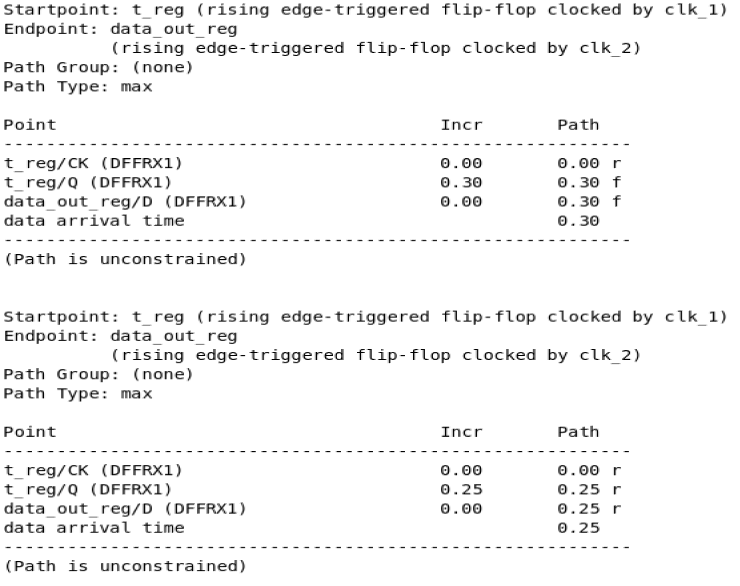
静态时序分析:SDC约束命令set_fasle_path详解
相关阅读
静态时序分析https://blog.csdn.net/weixin_45791458/category_12567571.html?spm1001.2014.3001.5482 目录
指定建立/保持时间检查
指定上升/下降沿
指定时序路径起点
删除虚假路径
添加注释
简单使用
写在最后 在之前的文章中,我们讨论了如何使…
持续集成(CICD)- Jenkins+Git+gogs综合实战(笔记二)
文章目录 七、拉取代码方法一:直接填写命令进行拉取(不建议用这种)方法二:使用源码管理拉取代码步骤一:确认环境(检查自己是否有Git插件)步骤二:构建项目时对项目的源码管理选择 Git步骤三:输入你仓库的SSH地址或者https地址,并且添加gitee的用户名和密方法一和方法二…
SpringCloud的Consul
0.介绍
Console是一款服务发现、健康检查、分布式配置中心,有单独的web可供配置和查看的Spring家族的一员。
1.下载
https://developer.hashicorp.com/consul/install?product_intentconsul
2.启动
consul agent-dev访问localhost:8500
3 Java使用注册中心
…
【李沐论文精读】GAN精读
论文:Generative adversarial nets 参考:GAN论文逐段精读、生成对抗网络、李沐视频精读系列 一、介绍 什么是GAN? GAN(Generative adversarial network,生成对抗网络),它由生成器G(Generator Neural Netwo…
Java 简单模拟银行存取钱
模拟银行存取钱 一、实验任务
在银行办理业务时,通常银行会开多个窗口,客户排队等候,窗口办理完业务,会呼叫下一个用户办理业务。本实验要求编写一个程序模拟银行存取钱业务办理。假如有两个用户在存取钱,两个用户分别…
力扣--动态规划413.等差数列划分
思路分析 :
开始时判断输入向量的大小是否小于等于2,若是,则返回0,因为少于3个元素不可能形成等差数列。初始化一个大小为n的动态规划数组dp,用于存储以每个位置为结尾的等差数列的数量。初始化一个变量result用于存储最终的结果…