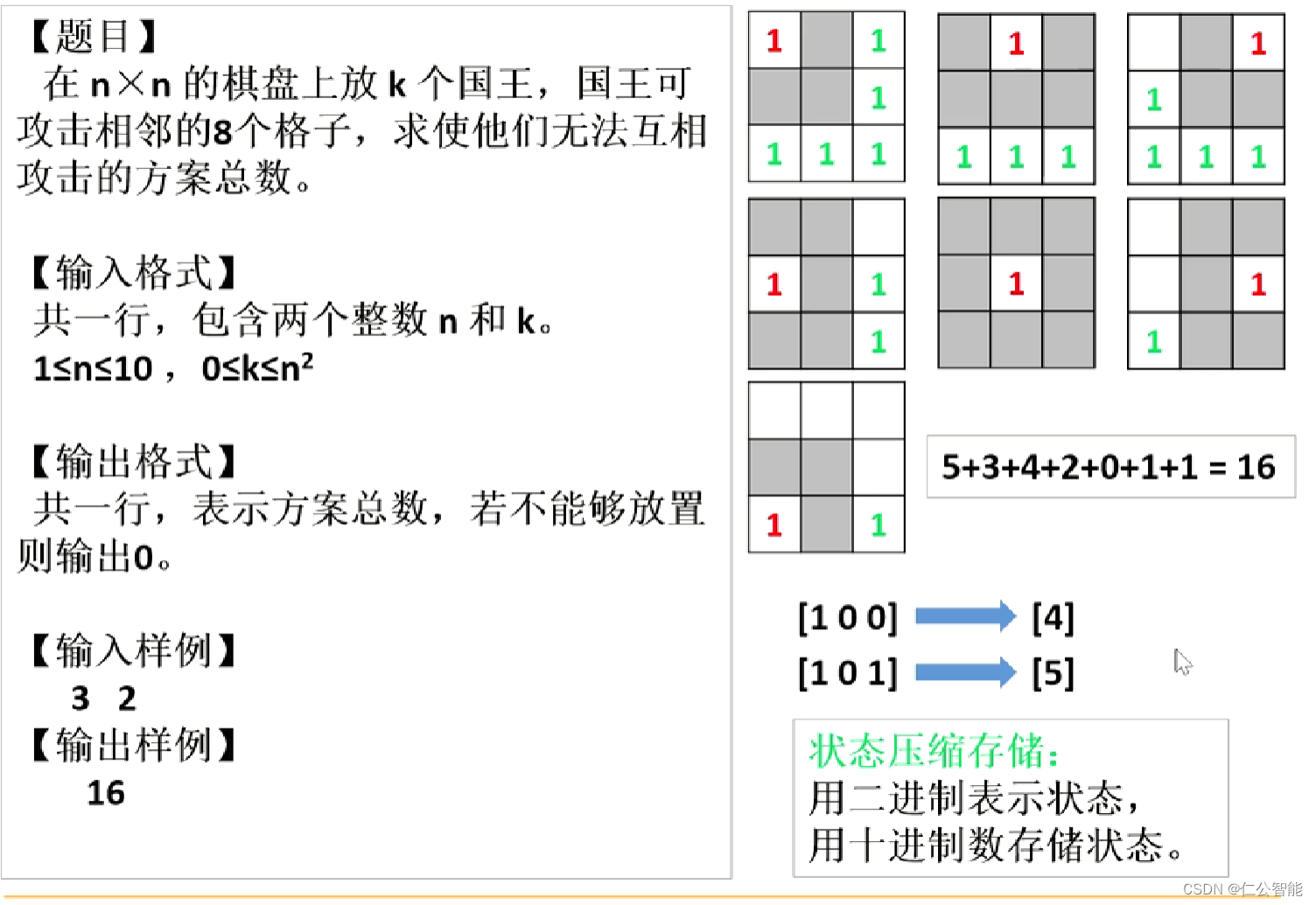
1、B站视频链接:E25 状态压缩DP 小国王_哔哩哔哩_bilibili
题目链接:[SCOI2005] 互不侵犯 - 洛谷



#include <bits/stdc++.h>
using namespace std;
int n,k;//棋盘行数、国王总数
int cnt;//一行合法状态的个数
int s[1<<12];//一行合法状态集,2的12次方钟状态
int num[1<<12];//每个合法状态包含的国王数
long long f[12][144][1<<12];
//f[i,j,a]//表示前i行已经放了j个国王,
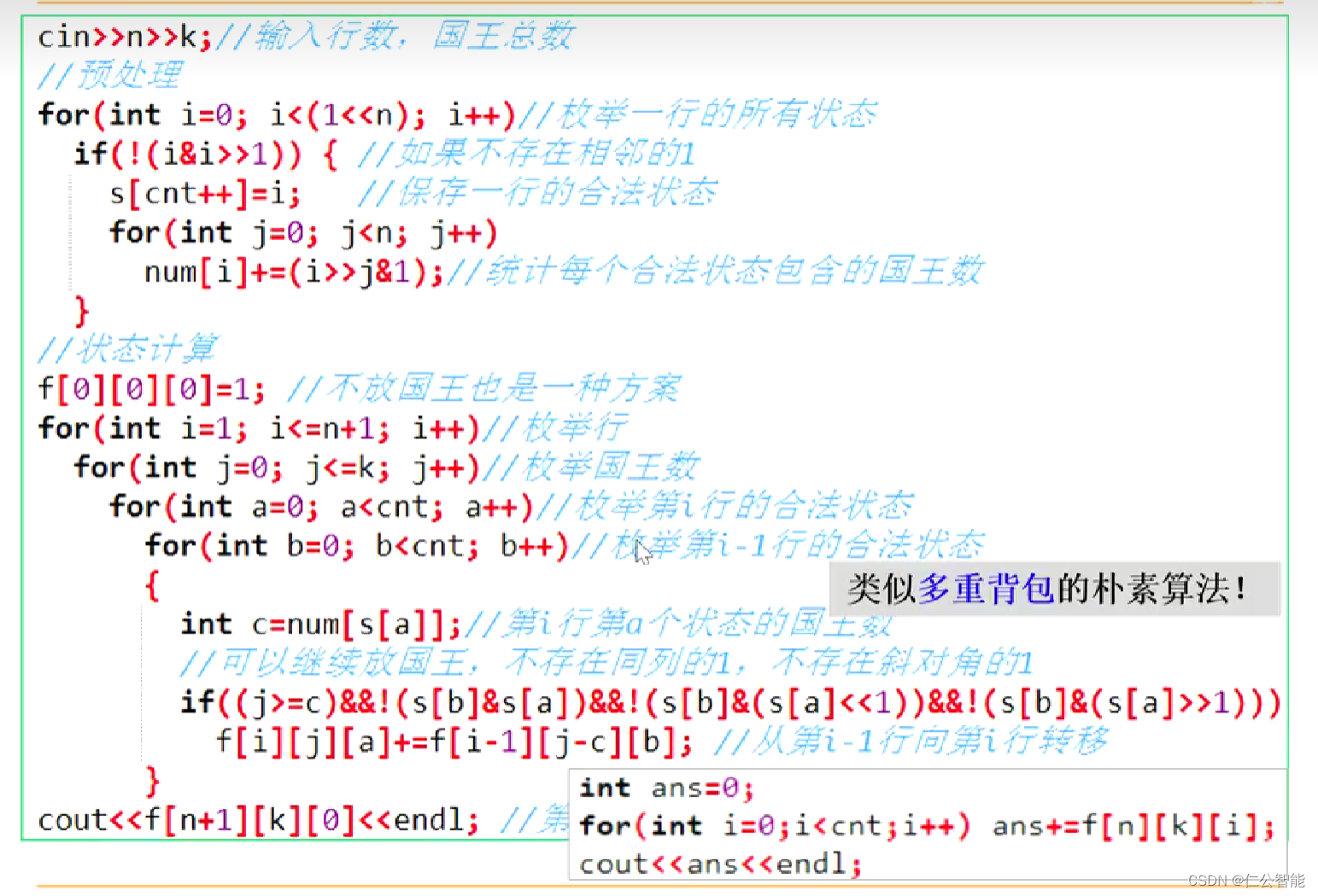
//第i行的第a个状态时的方案数int main(){cin>>n>>k;//预处理,选出合法状态和合法状态下的国王数 for(int i=0;i<(1<<n);i++){//枚举一行所有的状态 if(!(i&i>>1)){//如果不存在相邻的1 s[cnt++]=i;//记录一行合法的状态集 for(int j=0;j<n;j++){num[i]+=(i>>j&1);//每个合法状态包含的国王数 }}
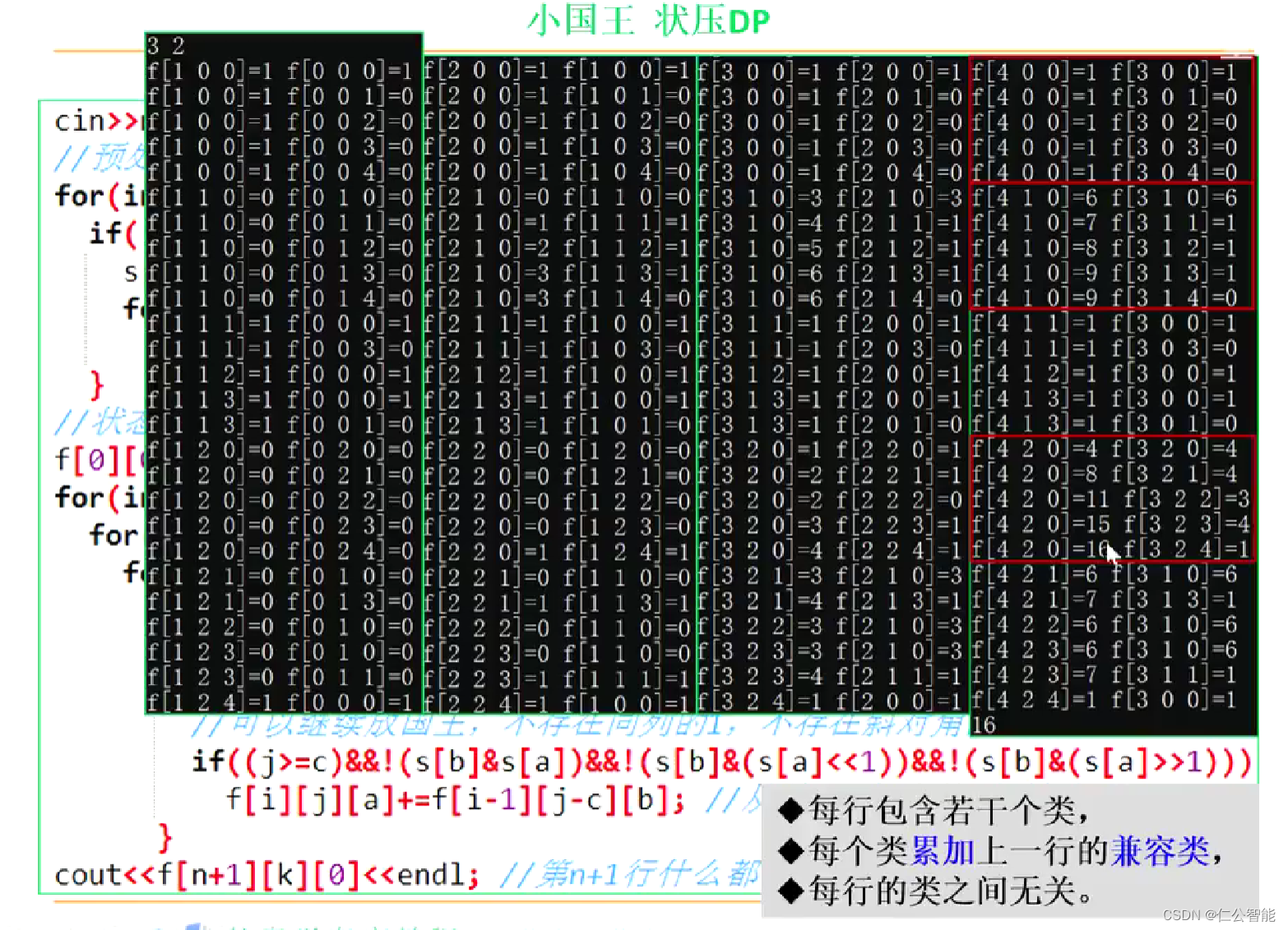
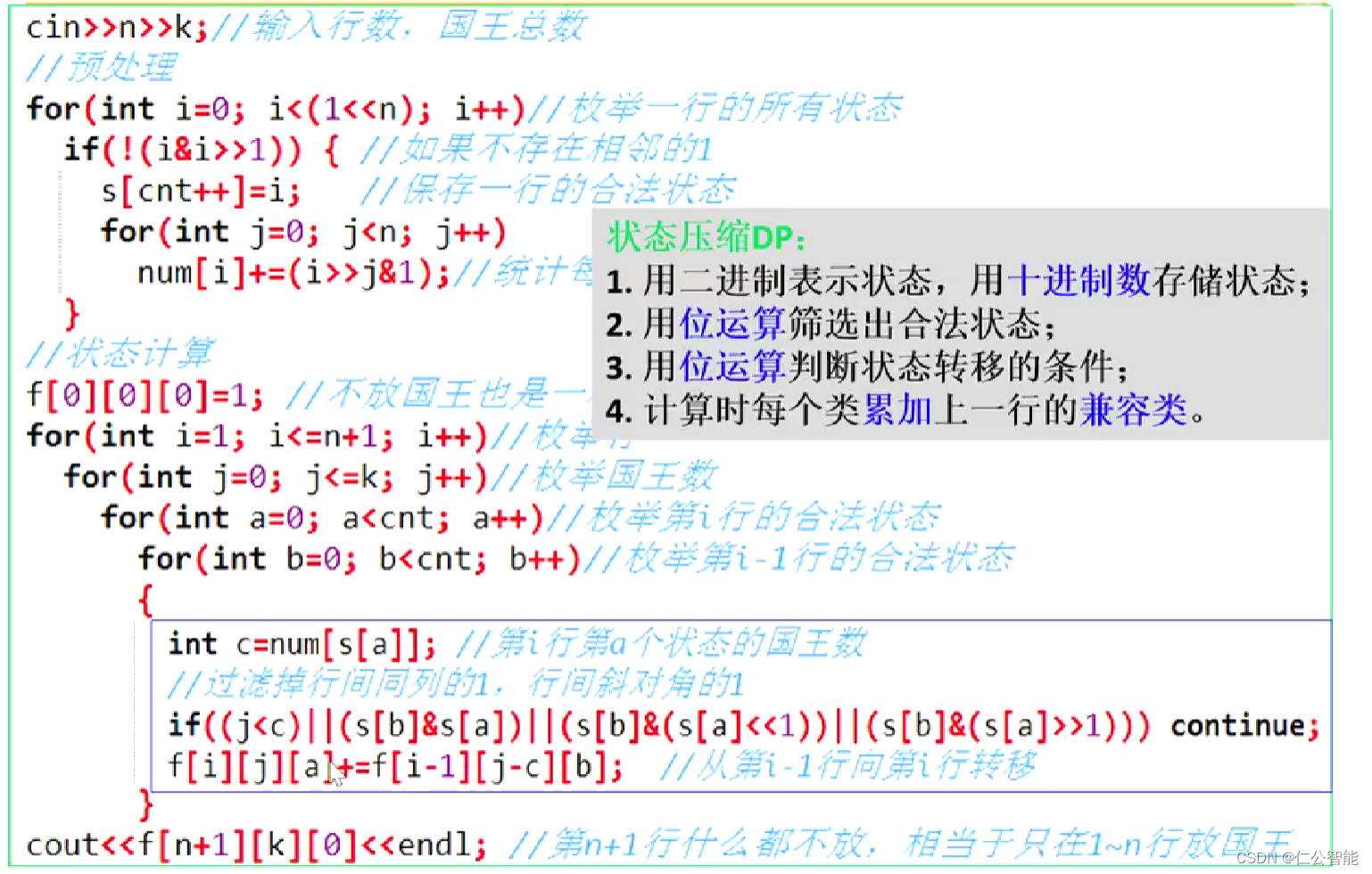
}f[0][0][0]=1;//边界 for(int i=1;i<=n+1;i++){//枚举行 for(int j=0;j<=k;j++){//枚举国王数 for(int a=0;a<cnt;a++){//枚举第i行的合法状态 for(int b=0;b<cnt;b++){//枚举第i-1行的合法状态 int c=num[s[a]];//第i行第a个状态的国王数if((j>=c) //可以继续放国王 &&!(s[b]&s[a])//不存在同列的1 &&!(s[b]&(s[a]<<1))//不存在写对角的1 &&!(s[b]&(s[a]>>1))){ f[i][j][a]+=f[i-1][j-c][b];//行间状态转移(累加求和) } }}}
} cout<<f[n+1][k][0]<<endl;//第n+1行不放国王的方案数,省去了累加步骤 return 0;
}
2、B站视频链接:E26 状态压缩DP 玉米田_哔哩哔哩_bilibili
题目链接:[USACO06NOV] Corn Fields G - 洛谷


#include <bits/stdc++.h>
using namespace std;
const int P=1e8;
int n,m;
int g[14];
int cnt;
int s[1<<14];
int f[14][1<<14];
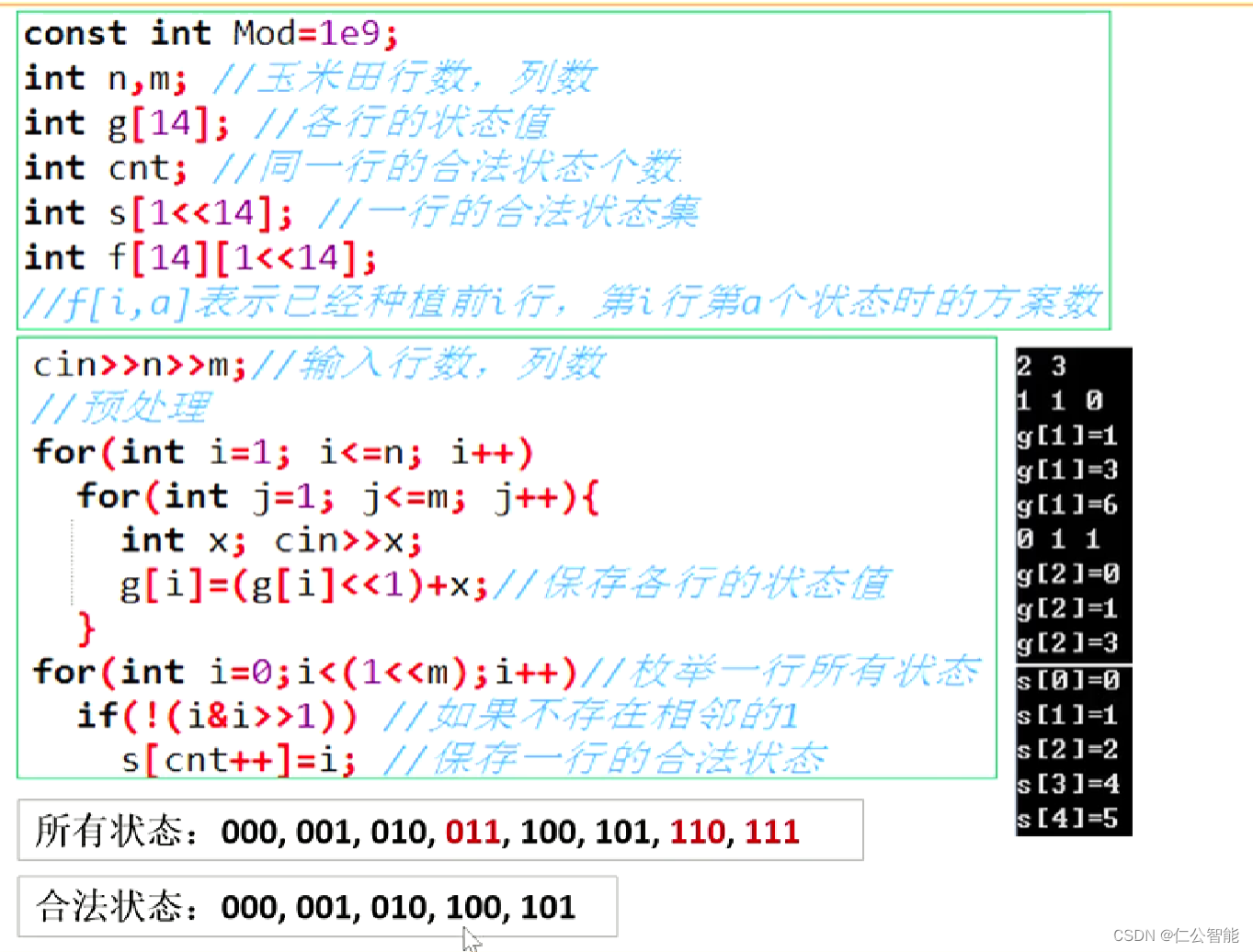
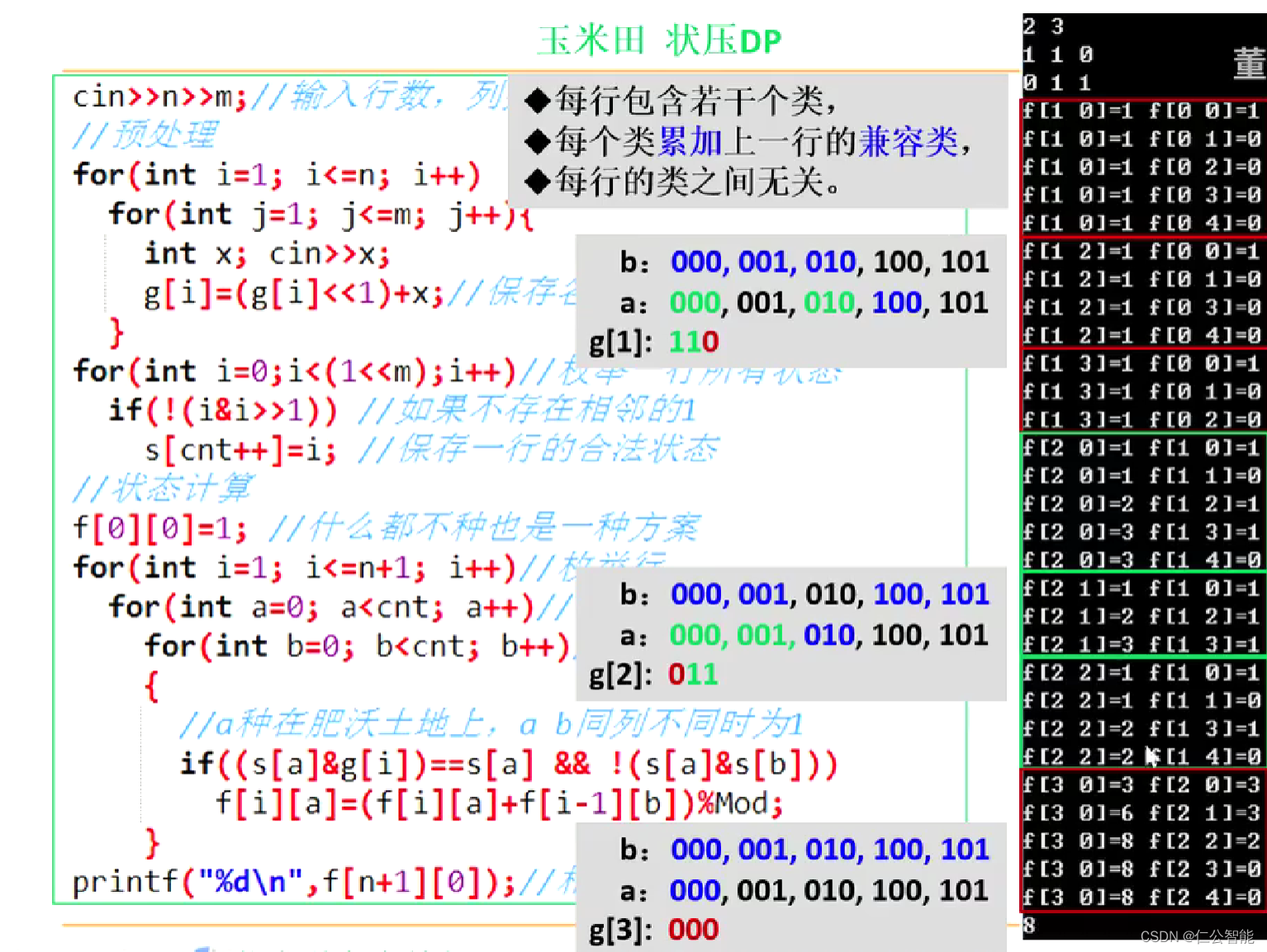
//f[i,a]表示已经种植前i行,第i行第a个状态的方案数int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){int x;cin>>x;g[i]=(g[i]<<1)+x;//各行的状态值(十进制) }}//预处理出合法状态for(int i=0;i<(1<<m);i++){//枚举状态,m列则有2的m次方种 if(!(i&i>>1)){//如果不存在相邻的1 s[cnt++]=i;} } f[0][0]=1;//状态计算for(int i=1;i<=n+1;i++){//枚举行 for(int a=0;a<cnt;a++){//枚举第i行的合法状态 for(int b=0;b<cnt;b++){//枚举第i-1行的 if(!(s[a]&s[b])//不能同列均为1 &&(s[a]&g[i])==s[a]){//种在肥沃土地上 f[i][a]=(f[i][a]+f[i-1][b])%P;}}}} printf("%d\n",f[n+1][0]);return 0;
} 3、B站视频链接:E27 状态压缩DP 炮兵部队_哔哩哔哩_bilibili
题目链接:[NOI2001] 炮兵阵地 - 洛谷
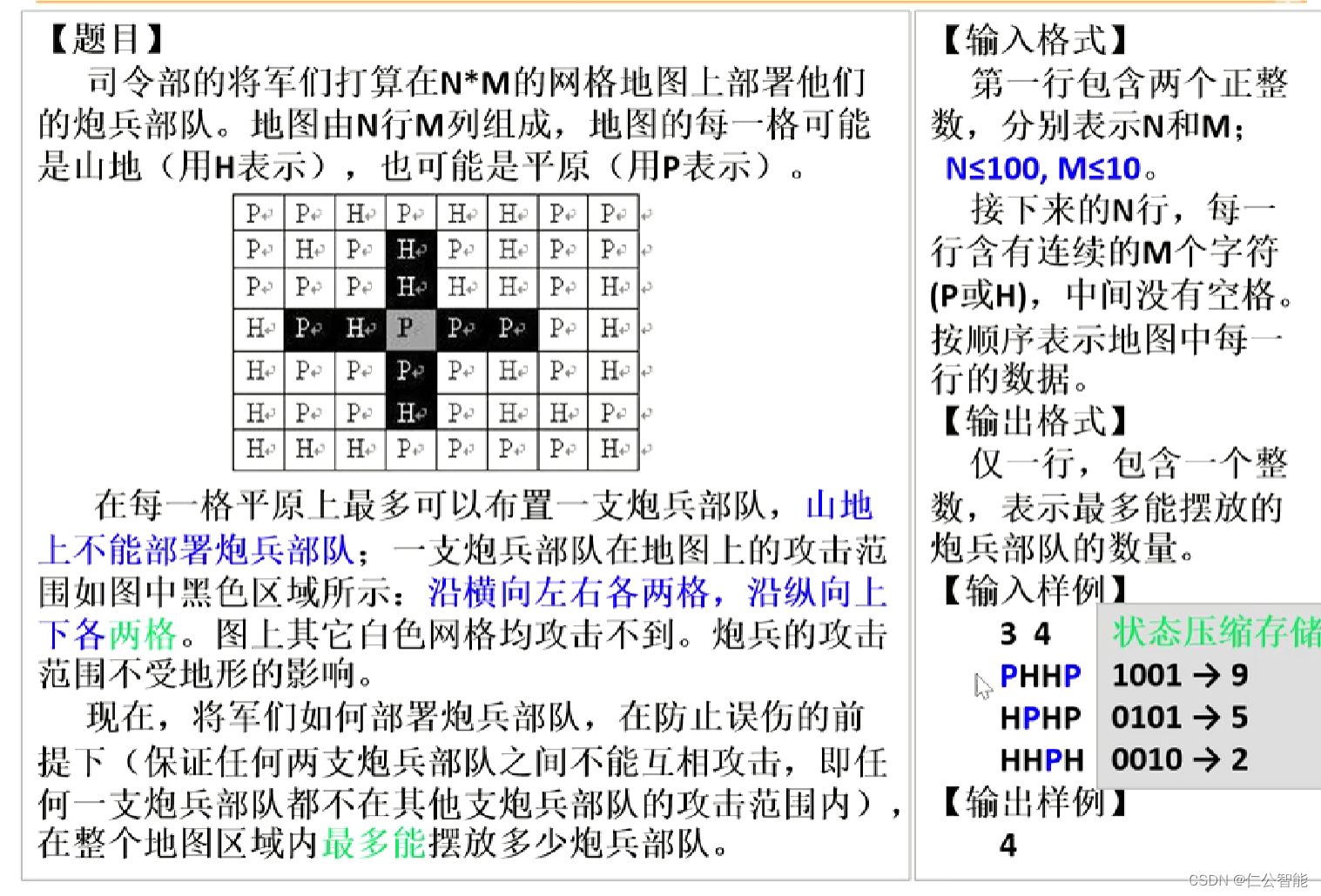
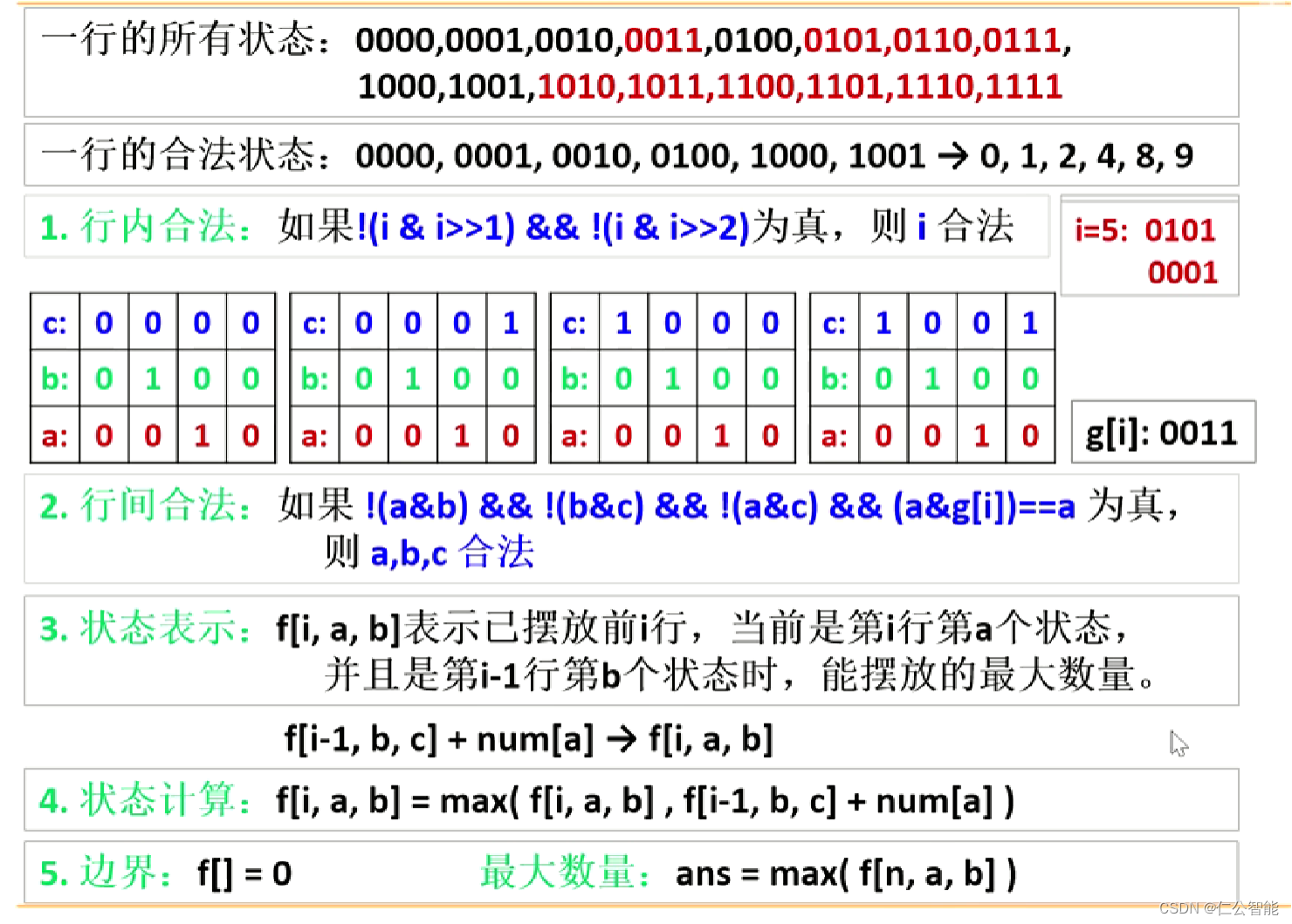
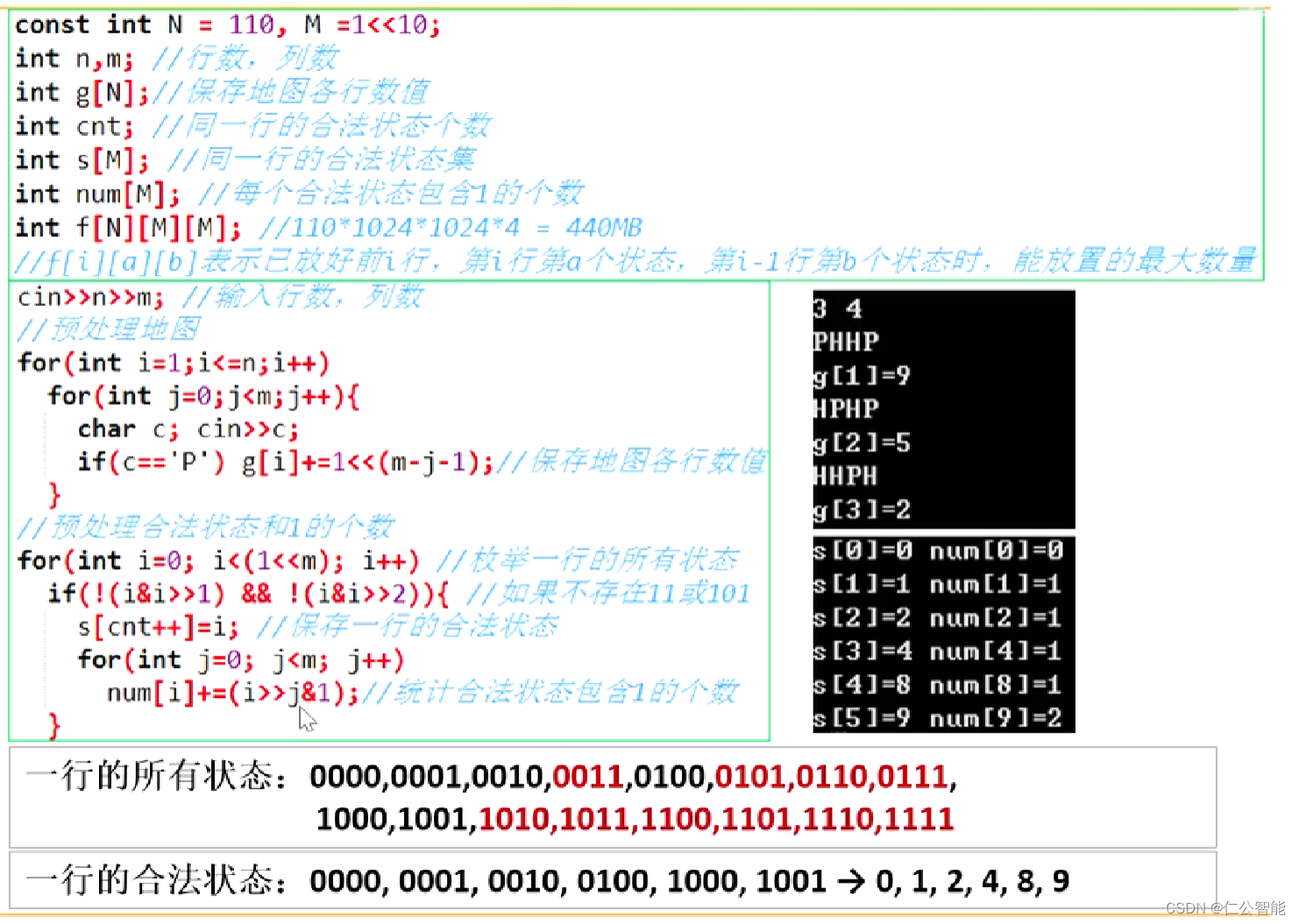
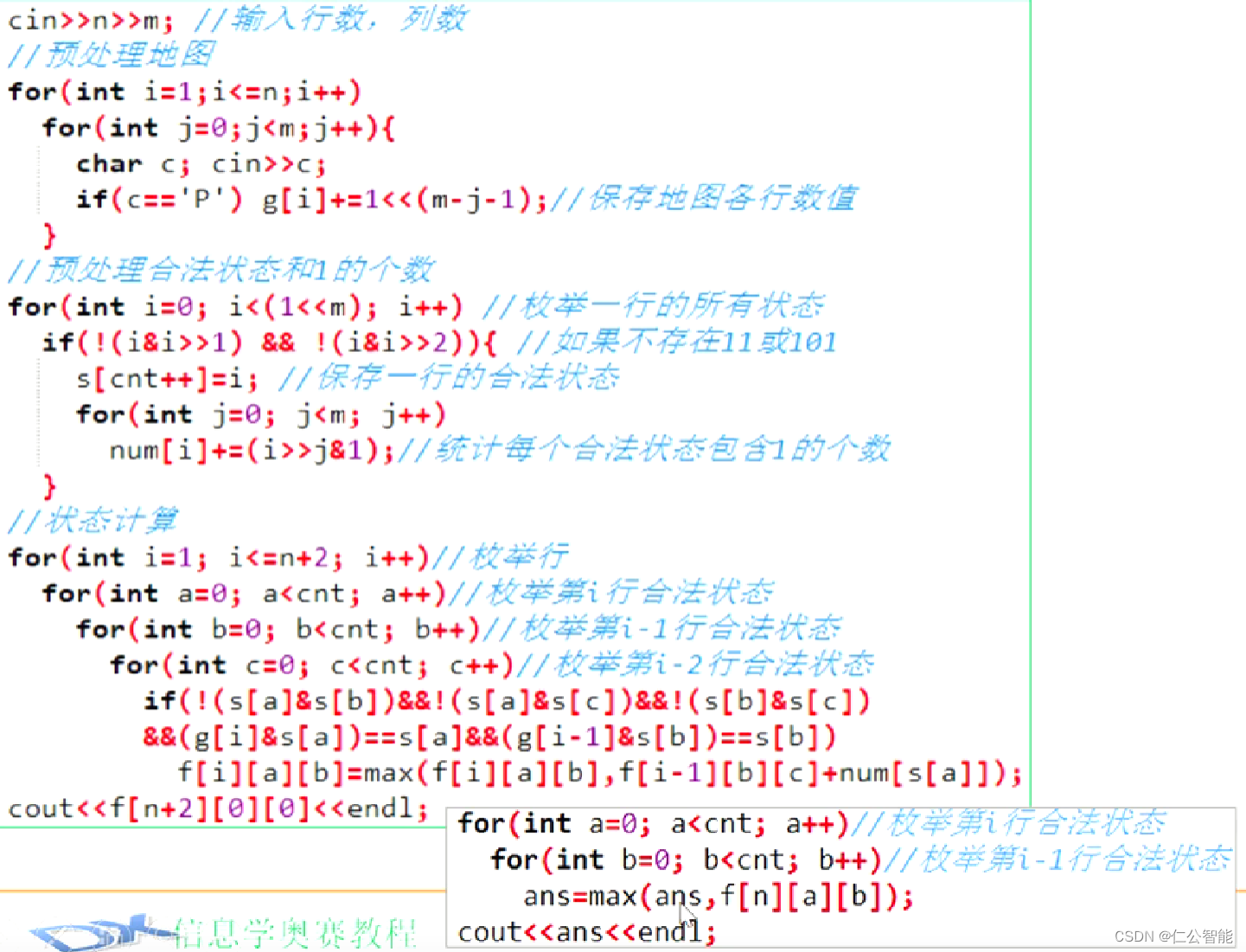
#include <bits/stdc++.h>
using namespace std;
const int N=110, M=1<<10;
int n,m; //行数,列数
int g[N]; //存储地图各行数值
int cnt; //一行的合法状态个数
int s[M]; //一行的合法状态集
int num[M]; //每个合法状态包含1的个数
int f[N][M][M]; //110*1024*1024*4 = 440MB
// f[i][a][b]表示已放好前i行,
// 第i行第a个状态,第i-1行第b个状态时,能放置的最大数量 int main(){cin>>n>>m;for(int i=1;i<=n;i++)for(int j=0;j<m;j++){char c; cin>>c; if(c=='P') g[i]+=1<<(m-j-1); //地图各行数值 }for(int i=0; i<(1<<m); i++) //枚举一行的所有状态 if(!(i&i>>1) && !(i&i>>2)){ //如果不存在11和101 s[cnt++]=i; //保存一行的合法状态for(int j=0; j<m; j++)num[i]+=(i>>j&1); //每个合法状态包含1的个数}for(int i=1; i<=n+2; i++) //枚举行for(int a=0; a<cnt; a++) //枚举第i行合法状态for(int b=0; b<cnt; b++) //枚举第i-1行合法状态for(int c=0; c<cnt; c++) //枚举第i-2行合法状态if(!(s[a]&s[b])&&!(s[a]&s[c])&&!(s[b]&s[c])&&(g[i]&s[a])==s[a]&&(g[i-1]&s[b])==s[b])f[i][a][b]=max(f[i][a][b],f[i-1][b][c]+num[s[a]]);cout<<f[n+2][0][0]<<endl;return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int N=110, M=1<<10;
int n,m; //行数,列数
int g[N]; //存储地图各行数值
int cnt; //一行的合法状态个数
int s[M]; //一行的合法状态集
int num[M]; //每个合法状态包含1的个数
int f[2][M][M]; //滚动数组 2*1024*1024*4 = 8MB
// f[i][a][b]表示已放好前i行,
// 第i行第a个状态,第i-1行第b个状态时,能放置的最大数量 int main(){cin>>n>>m;for(int i=1;i<=n;i++)for(int j=0;j<m;j++){char c; cin>>c; if(c=='P') g[i]+=1<<(m-j-1); //地图各行数值 }for(int i=0; i<(1<<m); i++) //枚举一行的所有状态 if(!(i&i>>1) && !(i&i>>2)){ //如果不存在11和101 s[cnt++]=i; //保存一行的合法状态for(int j=0; j<m; j++)num[i]+=(i>>j&1); //每个合法状态包含1的个数}for(int i=1; i<=n+2; i++) //枚举行for(int a=0; a<cnt; a++) //枚举第i行合法状态for(int b=0; b<cnt; b++) //枚举第i-1行合法状态for(int c=0; c<cnt; c++) //枚举第i-2行合法状态if(!(s[a]&s[b])&&!(s[a]&s[c])&&!(s[b]&s[c])&&(g[i]&s[a])==s[a]&&(g[i-1]&s[b])==s[b])f[i&1][a][b]=max(f[i&1][a][b],f[i-1&1][b][c]+num[s[a]]);cout<<f[n+2&1][0][0]<<endl;return 0;
}