堆排序是一种与插入排序和并归排序十分不同的算法。
优先级队列
Priority Queue
优先级队列是类似于常规队列或堆栈数据结构的抽象数据类型(ADT)。优先级队列中的每个元素都有一个相关联的优先级key。在优先级队列中,高优先级的元素优先于低优先级的元素。
虽然优先级队列通常使用堆heap实现,但它们在概念上与堆不同。优先级队列是一种抽象的数据结构,如列表或映射; 正如列表可以用链表或数组实现一样,优先级队列也可以用堆或其他方法(如有序数组)实现。
堆
Heap
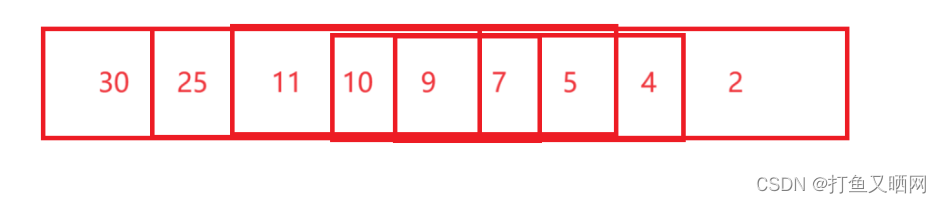
堆可以理解为由一个由数组来顺序存储的完全二叉树。
最大堆:任意节点的key ≥ 子节点的key
类似的
最小堆:任意节点的key ≤ 子节点的key
以最大堆为例,来讲解
最大堆
最大堆的操作
build_max_heap:根据一个未排序的数组生成一个最大堆
max_heapify: 如果子树的根节点违反最大堆的特性,就对其进行纠正。max_heapify的前提是子树的左右子树都是最大堆。
build_max_heap的伪代码:
for i = n/2 down to 1do max_heapify(A,i)max_heapify和build_max_heap的时间复杂度
对叶子结点上面一层的结点(level 1)进行max_heapify是O(1)的时间复杂度
对叶子结点上面i层 level i 的结点进行max_heapify是O(i)
n/4个结点是level 1,n/8个结点是level 2,n/16个结点是level 3 ... 1个结点是level logn
因此max_heapify的时间复杂度为O(logn),可计算出build_max_heap的时间复杂度为O(n)
计算过程在最底下
堆排序步骤
1.根据一个未排序的数组来创建最大堆
2.找到最大元素A[1]
3.交换元素A[n]和A[1],现在最大元素位于堆的尾部
4.移除A[n](最大元素),只需将存放堆的数组的大小减1
5.经过交换元素之后的堆也许违背了最大堆的定义,但是A[1]的孩子仍然是最大堆,因此进行max_heapify,经过修正后,整个堆就是最大堆;重复步骤2-5,n次。
class Solution {
public://堆是一个完全二叉树,因此适合使用顺序存储的方式。//堆排序步骤://1.根据一个未排序的数组来创建最大堆//2.找到最大元素A[1]//3.交换元素A[n]和A[1],现在最大元素位于堆的尾部//4.移除A[n](最大元素),存放堆的数组的大小减1//5.经过交换元素之后的堆也许违背了最大堆的定义,但是A[1]的孩子仍然是最大堆,因此进行max_heapify,经过修正后,整个堆就是最大堆;重复2-5,n次//时间复杂度O(nlogn)vector<int> sortArray(vector<int>& nums) {build_max_heap(nums);//堆排序int n = nums.size();while(n > 0){//重复n次//找到最大元素,并与堆末尾元素进行交换int max_elem = nums[0];nums[0] = nums[n-1];nums[n-1] = max_elem;--n;//移出末尾元素//进行max_heapifymax_heapify(nums, 0, n);}return nums;}void build_max_heap(vector<int>& nums){int size = nums.size();for(int i = size/2-1;i >= 0;--i){max_heapify(nums, i, size);}}void max_heapify(vector<int>& nums, int i, int size){//将A[i]修正为最大堆//A[i]的左孩子为A[2i+1],右孩子为A[2i+2]int left = (i<<1) + 1;int right = left + 1;int large = left;//默认较大元素为左节点while(large < size){if(right < size && nums[right] > nums[left]){//假如右结点大于左节点large = right;//记右结点为较大的}if(nums[i] < nums[large]){//假如父节点小于左右结点中较大的结点//将父节点与较大的结点进行交换,从而使父节点大于左右子结点,符合最大堆的约束int tmp = nums[i];nums[i] = nums[large];nums[large] = tmp;i = large;//i调节为其子结点largelarge = (i<<1)+ 1;//large调整为i的左子节点}else{break;}}}};