1.5 简述转置卷积的主要思想以及应用场景-编程知识

1.5 简述转置卷积的主要思想以及应用场景

普通的卷积主要思想：

普通的卷积操作可以形式化为一个矩阵乘法运算，即y=Ax（1-12）

其中，x和y分别是卷积的输入和输出(展平成一维向量形式)，维度分别为d⁽i⁾和d⁽⁰⁾；A是由卷积核、滑动步长决定的常对角矩阵，维度为其每一行对应着卷积核的一次滑动位置。以一维卷积为例，假设输入向量
$x=[a,b,c,d,e,f,g]^T$
卷积核为K=[x,y,z],卷积的滑动步长为2，则输出向量为

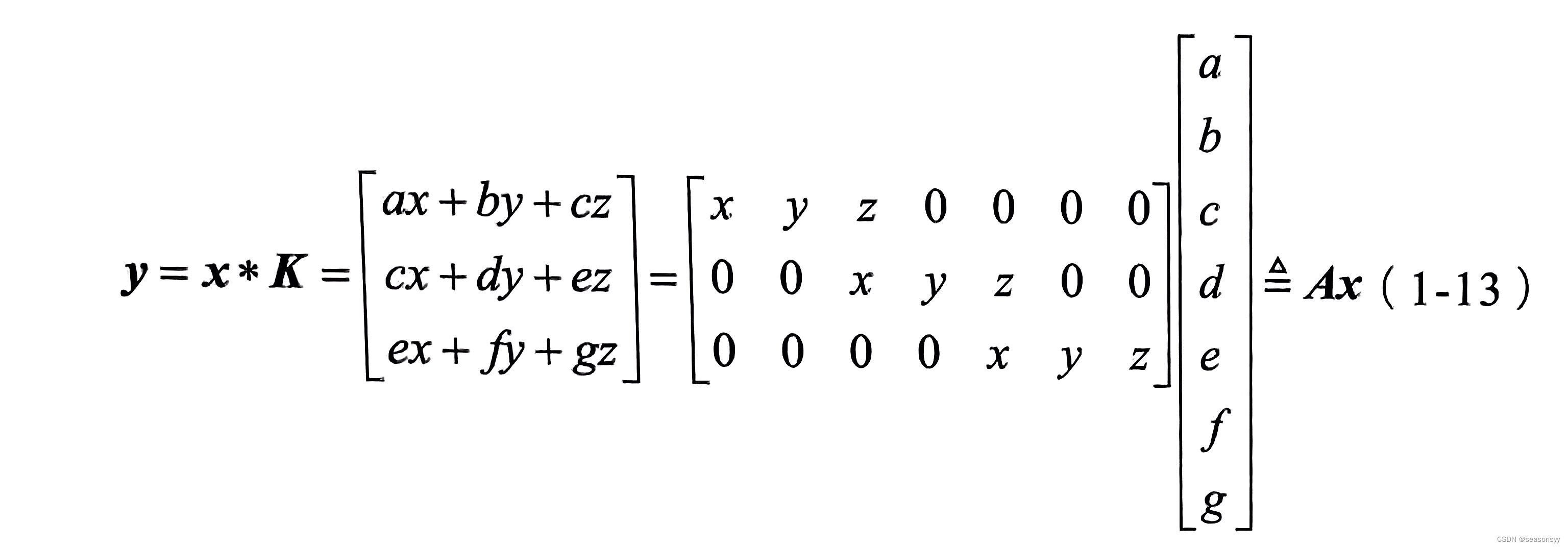
在这里插入图片描述

转置卷积主要思想：

反过来，记 $A^T$ 为矩阵A的转置，定义如下矩阵运算：

y^= $A ^T$ $x$ ^（1-14）

其所对应的操作被称为转置卷积，x^ 和 y^ 分别是转置卷积的输入和输出，维度分别为d⁽⁰⁾和d(i)。

转置卷积也被称为反卷积(deconvolution),它可以看作是普通卷积的一个“对称”操作，这种“对称性”体现在以下两个方面。

转置卷积能将普通卷积中输入到输出的尺寸变换逆反过来。

例如,式(1-12)中的普通卷积将特征图尺寸由d(1)变为d(1),而式(1-14)中的转置卷积则可以将特征图尺寸由d(0)复原为d(1)。这里需要注意的是，输入特征图经过普通卷积操作后再经过转置卷积，只是复原了形状，并不能复原具体的取值(因此将转置卷积称为反卷积并不是很合适)。
根据矩阵运算的求导知识，在式(1-12)所示的普通卷积中，输出y对于输入x的导数为
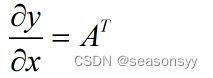
而在式(1-14)所示的转置卷积中，输出y^ 对于输入x^ 的导数为

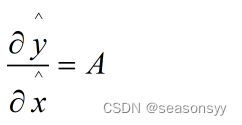
由此可以看出，转置卷积的信息正向传播与普通卷积的误差反向传播所用的矩阵相同，反之亦然。

以式(1-14)为例，我们可以写出转置卷积的具体计算公式：

可以看到，等号的右侧实际上就是一个普通卷积对应的矩阵乘法。

因此，转置卷积本质上就是一个对输入数据进行适当变换(补零/上采样)的普通卷积操作。

在具体实现时，以二维卷积为例，一个卷积核尺寸为Kw×Kh，滑动步长为(Sw，Sh)、边界填充尺寸为(pw，ph)的普通卷积，其所对应的转置卷积可以按如下步骤来进行。

对输入特征图进行扩张(上采样)：相邻的数据点之间，在水平方向上填充Sw-1个零，在垂直方向上填充Sn-1个零。

对输入特征图进行边界填充：左右两侧分别填充个零列，上下两侧分别填充个零行。

在变换后的输入特征图上做卷积核大小为、滑动步长为(1，1)的普通卷积操作。

在上述步骤2中，转置卷积的边界填充尺寸(pw^， pn^)是根据与之对应的普通卷积的边界填充尺寸(pw，pn)来确定的，很多深度学习框架(如PyTorch)就是按照这个思路来设定转置卷积的边界填充尺寸。

但在有些计算框架(如TensorFlow)中，做卷积时无法显式指定边界填充尺寸，只能选择一些预定义的填充模式(如padding=same或padding=valid)，此时，转置卷积的边界填充尺寸是根据与之对应的普通卷积的边界填充模式来设定的。

需要注意的是，当滑动步长大于1时，卷积的输出尺寸公式中含有向下取整操作，故而普通卷积层的输入尺寸与输出尺寸是多对一关系，此时转置卷积无法完全恢复之前普通卷积的输入尺寸，需要通过一个额外的参数来直接或间接地指定之前的输入尺寸，(如TensorFlow中的output_shape参数、PyTorch中的output_padding参数)。

应用场景：

普通卷积和转置卷积所处理的基本任务是不同的。前者主要用来做特征提取，倾向于压缩特征图尺寸；

转置卷积主要用于对特征图进行扩张或上采样，代表性的应用场景如下。

语义分割/实例分割等任务：由于需要提取输入图像的高层语义信息，网络的特征图尺寸一般会先缩小，进行聚合；此外，这类任务一般需要输出与原始图像大小一致的像素级分割结果，因而需要扩张前面得到的具有较高语义信息的特征图，这就用到了转置卷积。
一些物体检测、关键点检测任务，需要输出与源图像大小一致的热图。
图像的自编码器、变分自编码器、生成式对抗网络等。