【Leetcode】top 100 双指针-编程知识

283 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

分析：双指针初始为0；left指针找零值，right指针找非零值；由于需要保持非零元素的相对顺序，right只能在left的右边寻找（这里不要将right=left+1，会造成right的回退）结束循环条件 right < len(nums)；
class Solution(object):def moveZeroes(self, nums):""":type nums: List[int]:rtype: None Do not return anything, modify nums in-place instead."""i, j, m = 0, 0, len(nums)while j < m:   if nums[i] == 0:while j < m: if nums[j] != 0:  #j指向i后第一个非零值nums[i], nums[j] = nums[j], nums[i]break                  j+=1    i, j = i+1, j+1return nums

11 盛最多的水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

分析：双指针指向一头一尾，使宽度最大；

在移动指针时，宽度减小，只能通过用更大的高度值替换现有较小的高度值来增加水量；

当height[left] < height[right]时，移动left指针，若找到比height[left]更大的元素时，更新水量和left指针；

若找不到比height[left]更大的元素时，当前水量为最大；
class Solution(object):def maxArea(self, height):""":type height: List[int]:rtype: int"""out = min(height[0], height[-1]) * (len(height) - 1)left, right = 0, len(height) - 1while left < right:if height[left] < height[right]:           #移动左侧idx = left+1while idx < right:if height[idx] > height[left]:     #可能需要更新out = max(out, min(height[idx],height[right]) * (right-idx))breakidx+=1left = idxelse:idx = right-1while idx > left:if height[idx] > height[right]:     #可能需要更新out = max(out, min(height[idx],height[left]) * (idx-left))   breakidx-=1right = idxreturn out
官方思路：不在乎height[idx] 和 height[left] 的大小，反正left指针需要更新到height[left] > height[right]
class Solution(object):def maxArea(self, height):""":type height: List[int]:rtype: int"""left, right, out = 0, len(height) - 1, 0while left < right:if height[left] < height[right]:           out = max(out, height[left] * (right-left))left += 1else:out = max(out, height[right] * (right-left))   right -= 1return out
相当于用增加的idx内存换out更新次数的减少；

还有一个提前结束的条件： out >= max(height) * (right - left) 因为再更新也无法找到更大的高度值；

15 三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

分析：当固定nums[i]时，该问题转为在nums[i:]中找到两数之和为-nums[i]，可以搭配hashmap；

去重处理...本来想用set的自动去重，但list不满足可哈希条件，无法实现set(list)，这里list为二维或更高维列表...还是选择用hashmap：键用tuple，这里需要搭配排序使三元组中元素的相对位置一致；
class Solution(object):def threeSum(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""out = {}for i in range(len(nums)-1):hashmap = {}for j, num in enumerate(nums[i+1:]):if -nums[i]-num in hashmap:outt = [nums[i], num, -nums[i]-num]outt.sort()out[tuple(outt)] = jelse:hashmap[num] = j return list(out)#改变排序位置
class Solution(object):def threeSum(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""out = {}nums.sort()for i in range(len(nums)-1):hashmap = {}for j, num in enumerate(nums[i+1:]):if -nums[i]-num in hashmap:out[tuple([nums[i], num, -nums[i]-num])] = jelse:hashmap[num] = j return list(out)#时间复杂度过高O(nlogn)+O(n^2)+O(n)?
官方思路：同样先进行排序，再用一层循环固定一个值，将其转换为两数之和，这里要求固定的值不出现重复；在两数之和问题上使用一头一尾双指针，因为b+c=-a，随着b的增大c必然要减小，这里要求b的值不出现重复，自然c的值就不会出现重复；

优化点：提前结束条件：最小三个值的和大于0或最大三个值的和小于零
class Solution(object):def threeSum(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""nums.sort()if sum(nums[0:3])>0 or sum(nums[-3:])<0: return []out = []for i in range(len(nums)):if i>0 and nums[i] == nums[i-1]:continue               #nums[i]不重复left, right = i+1, len(nums)-1while left<right:if left>i+1 and nums[left]==nums[left-1]:          #nums[j]不重复left+=1continueif nums[left]+nums[right]<-nums[i]:left+=1elif nums[left]+nums[right]>-nums[i]:right-=1else:out.append([nums[i],nums[left],nums[right]])   left, right = left+1, right-1         return out

42 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

分析：用减法更方便计算

以 [a,b,c,d,e]为例：固定a时，要在[b,c,d,e]中找到>=a的第一个值（假设是c），故a-c蓄水ax1-b—ac宽度好计算，但需要用变量储存ac中间的体积；

固定c时，要在[d,e]中找到>=c的第一个值（假设不存在），故c无法作为较小的壁蓄水；改判断c作为较大的壁蓄水：在向右遍历时添加一个指向[d,e]第一个最大值的指针mid，同时也需要用变量储存c-mid中间的体积；
class Solution(object):def trap(self, height):""":type height: List[int]:rtype: int"""left, mid, right = 0, [1,0], [1,0]out = 0while left < len(height)-1:flag = 1while right[0] < len(height):if height[right[0]] >= height[left]:     #找到>=height[left]的值out += height[left]*(right[0]-left-1)-right[1]flag = 0breakelse:if height[right[0]] > height[mid[0]]:mid = right[:]           #mid更新right[0], right[1] = right[0]+1, right[1]+height[right[0]]if flag:                                    #遍历找不到>=height[left]的值out += height[mid[0]]*(mid[0]-left-1)-mid[1]left = mid[0]mid, right = [left+1, 0], [left+1, 0]else:left = right[0]mid, right = [left+1, 0], [left+1, 0]return out#时间复杂度太大，巨长的案例会超出时间限制
官方思路：

思路一：动态规划：对于下标 i 能接住的雨水为左侧最大值和右侧最大值的最小值减去 height[i]

用leftmax[i]代表[:i]的最大值，用rightmax[i]代表[i:]的最大值，

递推式：leftmax[i] = max( leftmax[i-1], height[i] )

rightmax[i] = max( rightmax[i+1], height[i] ) 这里发现rightmax适合倒序遍历

边界条件：leftmax[0] = height[0]

rightmax[-1] = height[-1]
class Solution(object):def trap(self, height):""":type height: List[int]:rtype: int"""leftmax, rightmax = [height[0]], [height[-1]]for i in range(1,len(height)):leftmax.append(max(leftmax[i-1], height[i]))rightmax.insert(0, max(rightmax[-i], height[-i-1]))#左右遍历合并out = 0for i in range(len(height)):out += min(leftmax[i], rightmax[i]) - height[i]return out
#return sum(min(leftmax[i], rightmax[i])-height[i] for i in range(n))
思路二：双指针：使用双指针来缩减动态规划中的空间开销；

因为对于下标 i 能接住的雨水为左侧最大值和右侧最大值的最小值减去 height[i]，所以已知左侧最大值和右侧最大值的大小关系时，该式可简化，对应更新left/right指针的下标即可；
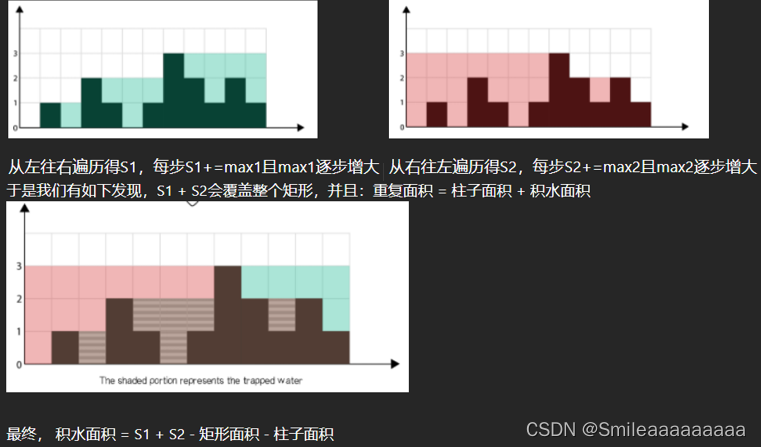
class Solution:def trap(self, height):out = 0left, right = 0, len(height) - 1leftmax = rightmax = 0while left < right:leftmax = max(leftmax, height[left])rightmax = max(rightmax, height[right])if leftmax < rightmax:                  out += leftmax - height[left]left += 1else:out += rightmax - height[right]right -= 1return out
思路三：两个方向计算当前最高值围成的有效面积，该面积=矩形面积+柱子面积+积水面积
class Solution(object):def trap(self, height):""":type height: List[int]:rtype: int"""# 同时从左往右和从右往左计算有效面积s1, s2 = 0, 0max1, max2 = 0, 0for i in range(len(height)):if height[i] > max1:max1 = height[i]if height[-i-1] > max2:max2 = height[-i-1]s1 += max1s2 += max2# 积水面积 = S1 + S2 - 矩形面积 - 柱子面积res = s1 + s2 - max1 * len(height) - sum(height)return res