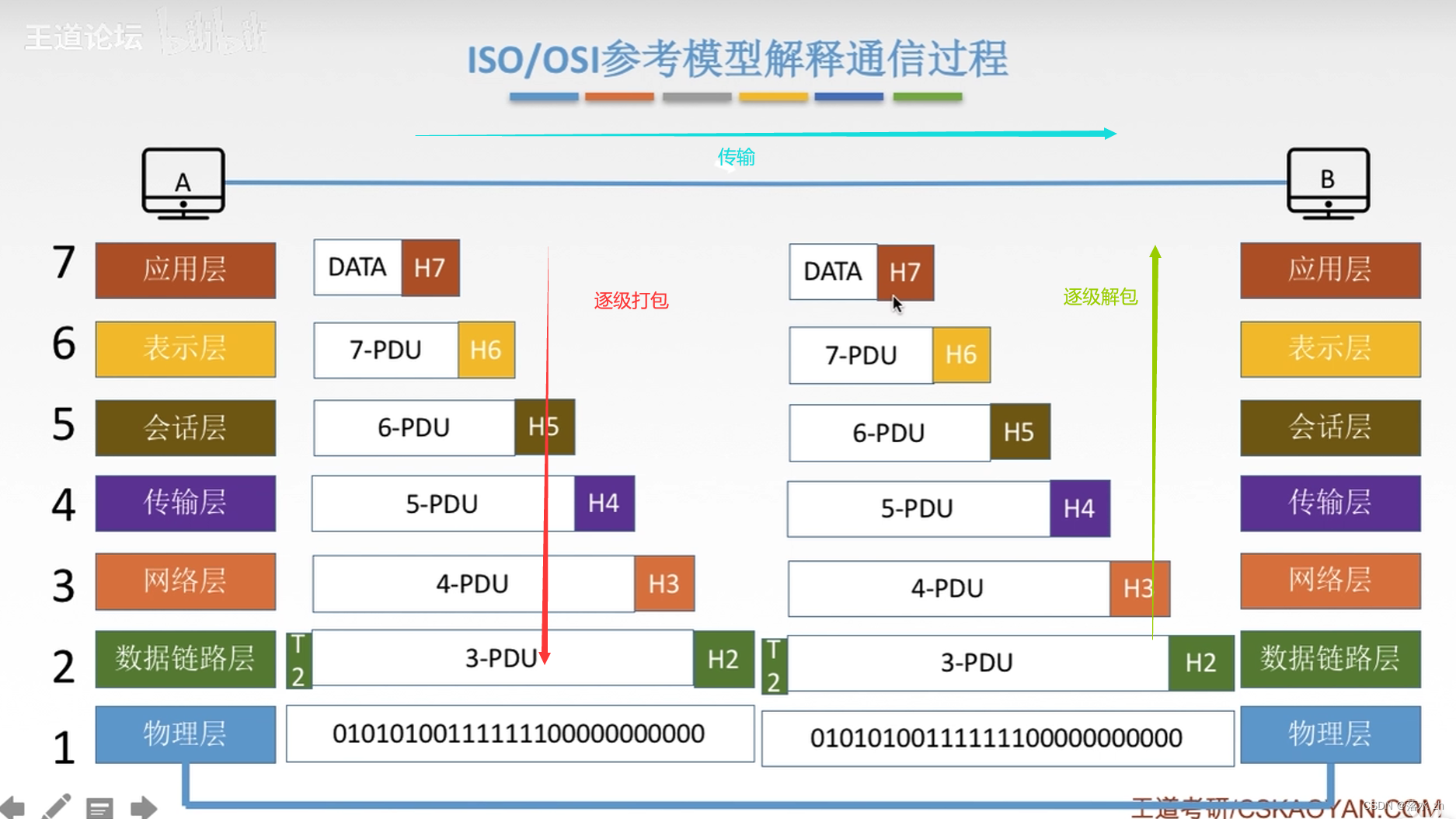
Logistic回归在医学科研、特别是观察性研究领域，无论是现况调查、病例对照研究、还是队列研究中都是大家经常用到的统计方法，而在影响因素研究筛选自变量时，大家习惯性用的比较多的还是先单后多，P＜0.05纳入多因素研究，很少用逐步回归法，有些同学可能听过但是了解也不多，这里先简单介绍一下。

那么什么时候推荐用逐步回归呢？有以下2种情况，可以考虑使用：

①构建预测模型时候，就放心大胆的用。其他场景，一般不建议用逐步回归法。

②探索性研究、探讨多个影响因素时，候选的影响因素实在太多（单因素分析后P值<0.05者，仍然超过10个），或者样本量不大。

逐步回归法的原理听上去很复杂，但是用R语言几行代码也可以搞定，只是R语言需要一定的代码基础，一时半会儿也无法学会，因此，这里结合实操案例为大家介绍一个智能在线免费统计分析平台——风暴统计。

一、实操数据介绍

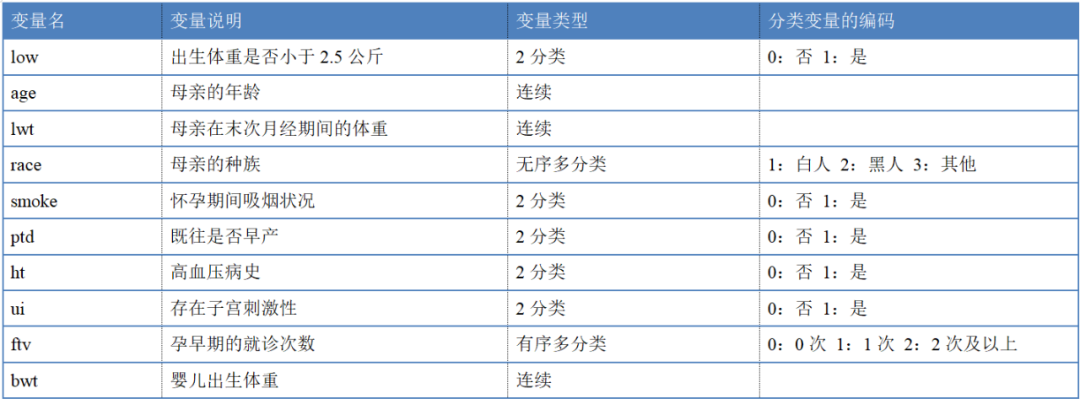
这里我们使用的是R语言自带数据集MASS中的birthwt，birthwt是一份与婴儿出生体重低相关的危险因素数据，其中包含的变量见下表，根据研究设计，以“low”作为结局变量。

二、风暴统计智能在线免费平台复现

目前风暴统计平台可以非常快速准确的完成logistic回归，只需2步!

• 选入回归自变量
  

• 选择自变量筛选方式
  

全部是菜单式操作，完成后，界面直接给出规范三线表结果！还可以随着变量的调整实时更新结果，在数据探索初期，可以节省不少工作量！在撰写报告时，也不用再手工绘制三线表，填写数据了！统计小白也可以轻松上手！

1.logistic回归自变量选择

首先，选入变量，包括因变量、定量自变量、分类自变量。

①因变量

这里因变量建议使用0和1进行表示，0代表阴性结局（如：未患病、二分类变量中值较小的组），1代表阳性结局（如：患病或二分类结局中值较大的组)。

②定量自变量

平台会将分类数大于5的变量自动归为定量自变量，并在选取定量自变量时，优先显示在上方，便于选取。

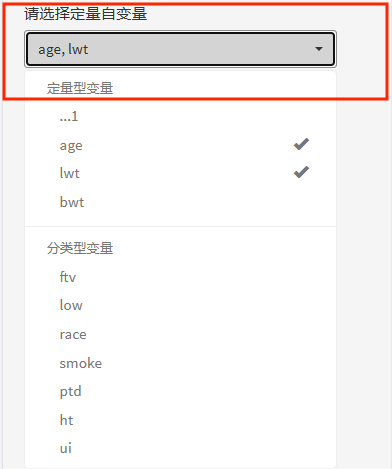
③分类自变量

同理，分类数小于5类的变量归入分类变量，在选取变量时，优先显示分类变量。

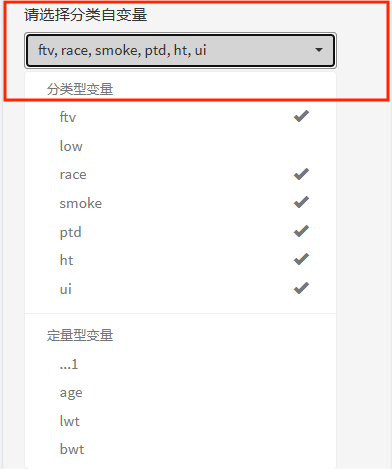
接着，选择自变量的筛选方式，包括先单后多法、逐步回归法。

2.选择自变量筛选方式

根据研究需要，如果需要开展先单后多的自变量筛选方式，那么“是否开展逐步回归分析”选择“否”。P阈值自行选择，如果自变量个数过少，可以适当放宽标准，0.1、0.2也都是可以的。当选择不限制时，选入的全部自变量都将纳入多因素回归分析。

如果需要选择逐步回归法，平台也提供了多种选择：双向逐步回归，向前逐步回归，向后逐步回归以及考虑到有时P值大于0.05的变量在逐步回归时也会留在模型中，新增了根据P<0.05的原则开展逐步回归！

这里我们选择单因素P<0.05的变量进入多因素开展逐步回归。

3.下载结果

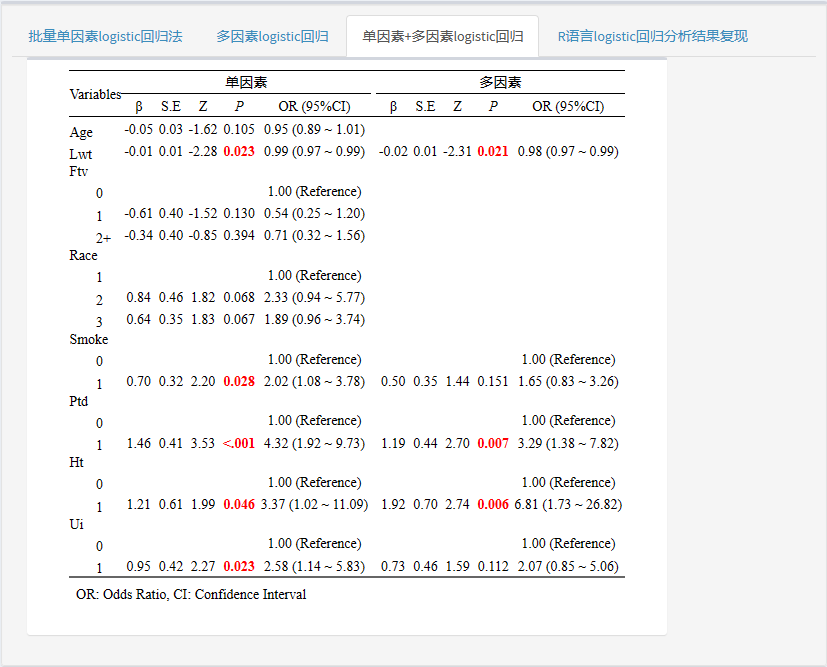
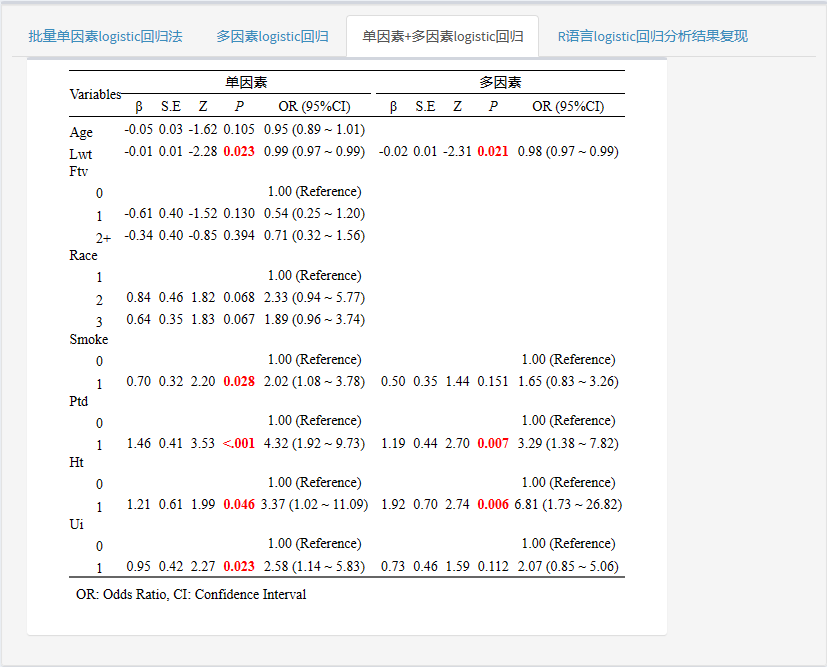
平台给出了多种结果展示，仅展示单因素回归结果，仅展示多因素回归结果，单因素+多因素显示在同一个表格中!

然后也可以选择小数位数，默认情况下，P值为3位小数，其他统计量为2位小数。

指定小数位数后，P值与统计量的小数位数将会统一。调整完成后，下载最终的三线表结果，平台支持下载excel或word！

三、R语言软件复现

这里采用autoReg包，autoReg包是一款功能十分强大的R包，不仅可以快捷完成基线表的制作，还可以直接一行代码输出回归分析（支持线性模型、广义线性模型和比例风险模型）的表格。

1.logistic回归模型构建

使用glm() 函数构建回归模型，glm(y~x1＋x2＋x3＋x4＋x......,data=数据集名，family="binomial")，指定因变量与自变量，设置数据集名。

logfit<-glm(low ~ age + lwt + race + smoke + ptd + ht + ui + ftv,data=bwt,family = "binomial")
summary(logfit)

此处参数family规定了回归模型的类型：family="binomial"指适用于二元离散因变量(binary)。

2.逐步回归法

autoReg逐步回归法的参数，就是Final=T 还是F，Final=T 提供逐步回归分析结果。另外，还有threshold，设定P值来挑选单因素分析的变量开展多因素回归。

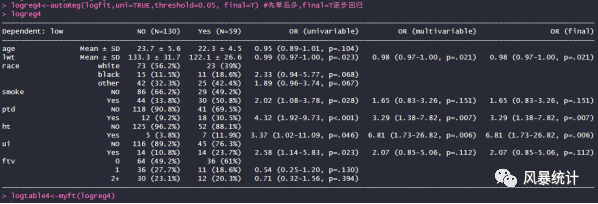
logreg4<-autoReg(logfit,uni=TRUE,threshold=0.05, final=T)   #final=T逐步回归
logreg4
logtable4<-myft(logreg4)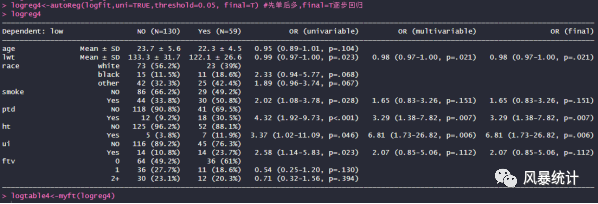

四、总结

通过对比，风暴统计与R语言先单后多的分析结果完全一致，风暴统计对于P值还有单独成列，结果更加清晰直观！这也是由于平台的构建依托于R代码进行分析。同时结果输出更加快捷，迅速，大家进行统计分析时不妨试一试！