一、基本概念
二叉搜索树(Binary Search Tree),又称为二叉查找树或二叉排序树,是一种具有特定性质的二叉树。
-
定义:二叉搜索树可以是一棵空树,也可以是具有以下特性的非空二叉树:
- 若其左子树不空,则左子树上所有结点的值均小于其根结点的值。
- 若其右子树不空,则右子树上所有结点的值均大于其根结点的值。
- 它的左、右子树也分别为二叉排序树。
-
结构:二叉搜索树是以二叉树的形式组织的,通常可以使用链表数据结构来表示。每个结点除了包含关键字(key)和可能的其他数据外,还包含指向其左孩子(lchild)和右孩子(rchild)的指针,以及指向其父结点(parent)的指针(如果需要的话)。如果某个孩子结点或父结点不存在,则相应属性的值为空(NIL)。
-
元素特性:二叉搜索树中存储的元素必须具备可比较性,例如整数(int)或浮点数(double)等。如果是自定义类型,需要指定比较方式。
-
应用:二叉搜索树作为一种经典的数据结构,具有链表快速插入与删除操作的特点和数组快速查找的优势。因此,它在许多场合下都有广泛的应用,如在文件系统和数据库系统中用于高效的排序与检索操作。
二叉搜索树是一种非常有效的数据结构,它能够保持数据的有序性,同时提供快速的查找、插入和删除操作。
二、插入操作实现
代码实现
# 定义树的节点
class BiTreeNode:def __init__(self, data):self.data = dataself.lchild = Noneself.rchild = Noneself.parent = Noneclass BST:def __init__(self): # 初始化二叉搜索树self.root = Nonedef insert(self, node, val): # 递归定义插入if not node:node = BiTreeNode(val) # 如果是空树,那么直接创建新的节点插入elif val < node.data: # 当插入的值小于根节点,就向左子树插入node.lchild = self.insert(node.lchild, val) # 调用递归函数实现插入节点node.lchild.parent = node # 并与父节点链接起来elif val > node.data: # 当插入的值大于根节点,就向右子树插入node.rchild = self.insert(node.rchild, val) # 调用递归函数实现插入节点node.rchild.parent = node # 并与父节点链接起来return nodedef insert_no_rec(self, val): # 非递归定义插入 在下面详细解释p = self.rootif not p: # 空树self.root = BiTreeNode(val) # 空树时直接新建节点插入即可returnwhile True:if val < p.data:if p.lchild: # 左孩子存在p = p.lchildelse: # 左孩子不存在时直接创建节点插入p.lchild = BiTreeNode(val)p.lchild.parent = pelif val > p.data:if p.rchild: # 右孩子存在p = p.rchildelse: # 右孩子不存在时直接创建节点插入p.rchild = BiTreeNode(val)p.rchild.parent = preturnelse:return非递归插入详细过程
使用非递归函数插入数据详细过程
1、随便定义一颗二叉搜索树(非空),将val = 12 插入到树中 。通过循环比较来实现数值的插入。
先将定义的 p 指针指向根节点,然后开始 val 与 根节点数值的比较。

2、 根据图中数值可知, val = 12 < p.data = 17,且 p点的左孩子 (p.lchild)存在,那么 p 指针向下移动,只执行 if val < p.data: 这块代码,变为如下图所示。
while True:if val < p.data:if p.lchild:p = p.lchildelse:p.lchild = BiTreeNode(val)p.lchild.parent = p 
3.此时, val = 12 < p.data = 13,且 p点的左孩子 (p.lchild)存在,执行 p = p.lchild 语句,那么 p 指针向下移动,变为如下图所示。

4.此时, val = 12 > p.data = 7, 那么他要往右子树进行插入,且p.data 的右孩子不存在,就直接创建新的节点进行插入即可。
elif val > p.data:if p.rchild: # 右孩子存在p = p.rchildelse: # 右孩子不存在时直接创建节点插入p.rchild = BiTreeNode(val)p.rchild.parent = preturn最后插入结果为:

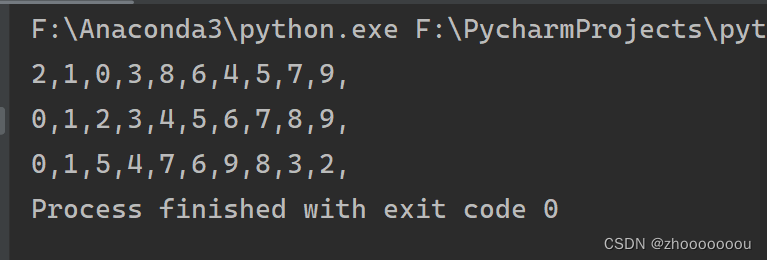
测试结果
对定义的函数进行测试,分别以先序,中序,后序输出。中序遍历都是从小到大输出,可以用作一种排序。
import random
class BiTreeNode:def __init__(self, data):self.data = dataself.lchild = Noneself.rchild = Noneself.parent = Noneclass BST:def __init__(self, li=None):self.root = Noneif li:for val in li:self.insert_no_rec(val)def insert(self, node, val): # 递归定义插入if not node:node = BiTreeNode(val)elif val < node.data:node.lchild = self.insert(node.lchild, val)node.lchild.parent = nodeelif val > node.data:node.rchild = self.insert(node.rchild, val)node.rchild.parent = nodereturn nodedef insert_no_rec(self, val):p = self.rootif not p: # 空树self.root = BiTreeNode(val)returnwhile True:if val < p.data:if p.lchild:p = p.lchildelse:p.lchild = BiTreeNode(val)p.lchild.parent = pelif val > p.data:if p.rchild:p = p.rchildelse:p.rchild = BiTreeNode(val)p.rchild.parent = preturnelse:returndef pre_order(self, root):if root:print(root.data, end=",")self.pre_order(root.lchild)self.pre_order(root.rchild)def in_order(self, root):if root:self.in_order(root.lchild)print(root.data, end=",")self.in_order(root.rchild)def post_order(self, root):if root:self.post_order(root.lchild)self.post_order(root.rchild)print(root.data, end=",")li = list(range(0, 10))
random.shuffle(li)tree = BST(li)
tree.pre_order(tree.root) # 先序
print(" ")
tree.in_order(tree.root) # 中序
print(" ")
tree.post_order(tree.root) # 后序输出结果