离散系统描述模型及其转换
常用离散模型 \textbf{常用离散模型} 常用离散模型
系统传递函数模型 t f \bf{tf} tf
H ( z ) = Y ( z ) X ( z ) = b 0 + b 1 z − 1 + . . . + b M z − M 1 + a 1 z − 1 + a 2 z − 2 + . . . + a N z − N H(z)=\frac{Y(z)}{X(z)}=\frac{b_0+b_1z^{-1}+...+b_Mz^{-M}}{1+a_1z^{-1}+a_2z^{-2}+...+a_Nz^{-N}} H(z)=X(z)Y(z)=1+a1z−1+a2z−2+...+aNz−Nb0+b1z−1+...+bMz−M
零-极点增益模型 z p k \bf{zpk} zpk
对系统传递函数进行分解得到:
H ( z ) = k ( z − q 1 ) ( z − q 2 ) . . . ( z − q M ) ( z − p 1 ) ( z − p 2 ) . . . ( z − p N ) H(z)=k\frac{(z-q_1)(z-q_2)...(z-q_M)}{(z-p_1)(z-p_2)...(z-p_N)} H(z)=k(z−p1)(z−p2)...(z−pN)(z−q1)(z−q2)...(z−qM)
极点留数模型 r p k \bf{rpk} rpk
当zpk中模型均是单极点时:
H ( z ) = r 1 1 − p 1 z − 1 + r 2 1 − p 2 z − 1 + . . . + r N 1 − p N z − 1 + k 0 H(z)=\frac{r_1}{1-p_1z^{-1}}+\frac{r_2}{1-p_2z^{-1}}+...+\frac{r_N}{1-p_Nz^{-1}}+k_0 H(z)=1−p1z−1r1+1−p2z−1r2+...+1−pNz−1rN+k0
二次分式模型 s o s \bf{sos} sos
离散系统中经常包含复数的极零点,将每一对共轭极零点多项式合并:
H ( z ) = g ∏ k = 1 l b 0 k + b 1 k z − 1 + b 2 k z − 2 1 + a 1 k z − 1 + a 2 k z − 2 H(z)=g\prod\limits_{k=1}^l\frac{b_{0k}+b_{1k}z^{-1}+b_{2k}z^{-2}}{1+a_{1k}z^{-1}+a_{2k}z^{-2}} H(z)=gk=1∏l1+a1kz−1+a2kz−2b0k+b1kz−1+b2kz−2
状态变量模型 s s \bf{ss} ss
系统状态方程:
{ W ( n + 1 ) = A W ( n ) + X ( n ) Y ( n ) = C W ( n ) + D X ( n ) \begin{cases} W(n+1)=AW(n)+X(n)\\ Y(n ) =CW(n)+DX(n)\end{cases} {W(n+1)=AW(n)+X(n)Y(n)=CW(n)+DX(n)
表示为传递函数:
H ( z ) = Y ( z ) X ( z ) = C W ( z ) X ( z ) + D = C ( z I − A ) − 1 B + D H(z)=\frac{Y(z)}{X(z)}=C\frac{W(z)}{X(z)}+D=C(zI-A)^{-1}B+D H(z)=X(z)Y(z)=CX(z)W(z)+D=C(zI−A)−1B+D
例题
- tf模型和zpk模型之间的转换
tf2zp()
对于 H ( z ) = 10 z − 1 1 − 3 z − 1 + 2 z − 2 H(z)=\frac{10z^{-1}}{1-3z^{-1}+2z^{-2}} H(z)=1−3z−1+2z−210z−1,求解零点向量z,极点向量p和增益系数k
%使用tf2zp();b = [0 10 0];
a = [1 -3 2];[z,p,k] = tf2zp(b,a);
disp('z=');disp(z);
disp('p=');disp(p);
disp('k=');disp(k);
得到结果:
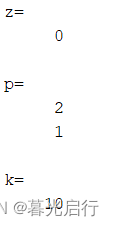
可得: H ( z ) = 10 ( z − 0 ) ( z − 2 ) ( z − 1 ) H(z)=10\frac{(z-0)}{(z-2)(z-1)} H(z)=10(z−2)(z−1)(z−0)
- zpk模型和tf模型之间的转换
zp2tf()
对于 H ( z ) = 5 ( z − 1 ) ( z + 3 ) ( z − 2 ) ( z + 4 ) H(z)=5\frac{(z-1)(z+3)}{(z-2)(z+4)} H(z)=5(z−2)(z+4)(z−1)(z+3),求传递函数模型
%使用zp2tf();
clear;
z = [1 -3]';
p = [2 -4]';
k = 5;[b,a] = zp2tf(z,p,k);disp('b=');disp(b);
disp('a=');disp(a);
得到结果:

可得: H ( z ) = 5 + 10 z − 1 − 15 z − 2 1 + 2 z − 1 − 8 z − 2 H(z)=\frac{5+10z^{-1}-15z^{-2}}{1+2z^{-1}-8z^{-2}} H(z)=1+2z−1−8z−25+10z−1−15z−2
- tf模型 和 sos模型之间的转换
tf2sos()
将 H ( z ) = 1.9 + 2.5 z − 1 + 2.5 z − 2 + 1.9 z − 3 1 − 6 z − 1 + 5 z − 2 − 0.4 z − 3 H(z)=\frac{1.9+2.5z^{-1}+2.5z^{-2}+1.9z^{-3}}{1-6z^{-1}+5z^{-2}-0.4z^{-3}} H(z)=1−6z−1+5z−2−0.4z−31.9+2.5z−1+2.5z−2+1.9z−3转化为二次分式形式
% 使用tf2sos
clear;
b = [1.9 2.5 2.5 1.9];
a = [1 -6 5 -0.4];[sos,g] = tf2sos(b,a);disp('sos=');disp(sos);
disp('g=');disp(g);

可得: H ( z ) = 1.9 ⋅ 1 + z − 1 1 − 5.0198 z − 1 ⋅ 1 + 0.3158 z − 1 + z − 2 1 − 0.9802 z − 1 + 0.0797 z − 2 H(z)=1.9·\frac{1+z^{-1}}{1-5.0198z^{-1}}·\frac{1+0.3158z^{-1}+z^{-2}}{1-0.9802z^{-1}+0.0797z^{-2}} H(z)=1.9⋅1−5.0198z−11+z−1⋅1−0.9802z−1+0.0797z−21+0.3158z−1+z−2
- sos模型 和 tf模型之间的转换
sos2tf()
将 H ( z ) = 4 ⋅ 1 + z − 1 1 − 0.5 z − 1 ⋅ 1 − 1.4 z − 1 + 1 1 + 0.9 z − 1 + 0.8 z − 2 H(z)=4·\frac{1+z^{-1}}{1-0.5z^{-1}}·\frac{1-1.4z^{-1}+1}{1+0.9z^{-1}+0.8z^{-2}} H(z)=4⋅1−0.5z−11+z−1⋅1+0.9z−1+0.8z−21−1.4z−1+1转化为tf模型
% 使用sos2tf()
clear;
sos = [1 1 0 1 -0.5 0;1 -1.4 1 1 0.9 0.8];
g = 4;[b,a] = sos2tf(sos,g);disp('b=');disp(b);
disp('a=');disp(a);

可得: H ( z ) = 4 − 1.6 z − 1 − 1.6 z − 2 + 4 z − 3 1 + 0.4 z − 1 + 0.35 z − 2 − 0.4 z − 3 H(z)=\frac{4-1.6z^{-1}-1.6z^{-2}+4z^{-3}}{1+0.4z^{-1}+0.35z^{-2}-0.4z^{-3}} H(z)=1+0.4z−1+0.35z−2−0.4z−34−1.6z−1−1.6z−2+4z−3
- zpk模型与sos模型之间的转换
zp2sos()
将 H ( z ) = 5 ( z − 1 ) ( z + 3 ) ( z − 2 ) ( z + 4 ) H(z)=5\frac{(z-1)(z+3)}{(z-2)(z+4)} H(z)=5(z−2)(z+4)(z−1)(z+3)转化为二次分式模型
clear;z = [1 -3]';
p = [2 -4]';
k = 5;[sos,g]=zp2sos(z,p,k);
disp('sos=');disp(sos);
disp('g=');disp(g);

可得: H ( z ) = 5 ⋅ 1 + 2 z − 1 − 3 z − 2 1 + 2 z − 1 − 8 z − 2 H(z)=5·\frac{1+2z^{-1}-3z^{-2}}{1+2z^{-1}-8z^{-2}} H(z)=5⋅1+2z−1−8z−21+2z−1−3z−2
- sos模型与zpk模型之间的转换
sos2zp()
将 H ( z ) = 1.9 ⋅ 1 + z − 1 1 − 5.0198 z − 1 ⋅ 1 + 0.3158 z − 1 + z − 2 1 − 0.9802 z − 1 + 0.0797 z − 2 H(z)=1.9·\frac{1+z^{-1}}{1-5.0198z^{-1}}·\frac{1+0.3158z^{-1}+z^{-2}}{1-0.9802z^{-1}+0.0797z^{-2}} H(z)=1.9⋅1−5.0198z−11+z−1⋅1−0.9802z−1+0.0797z−21+0.3158z−1+z−2转化为零-极点增益模型
% 使用sos2zp()
clear;sos = [1 1 0 1 -5.0198 0;1 0.3158 1 1 -0.9802 0.0797];
g = 1.9;[z,p,k] = sos2zp(sos,g);
disp('z=');disp(z);
disp('p=');disp(p);
disp('k=');disp(k);

可得: H ( z ) = 1.9 ⋅ z + 1 z − 5.0198 ⋅ z + 0.1579 − 0.9875 i z − 0.8907 ⋅ z − 0.1579 + 0.9875 i z − 0.0895 H(z)=1.9·\frac{z+1}{z-5.0198}·\frac{z+0.1579-0.9875i}{z-0.8907}·\frac{z-0.1579+0.9875i}{z-0.0895} H(z)=1.9⋅z−5.0198z+1⋅z−0.8907z+0.1579−0.9875i⋅z−0.0895z−0.1579+0.9875i
- tf模型与rpk模型之间的转换
residuez()
将 H ( z ) = 10 z − 1 1 − 3 z − 1 + 2 z − 2 H(z)=\frac{10z^{-1}}{1-3z^{-1}+2z^{-2}} H(z)=1−3z−1+2z−210z−1转化为极点留数模型
% 使用residuez()
clear;
b = [0 10 0];
a = [1 -3 2];[r,p,k] = residuez(b,a);disp('r=');disp(r);
disp('p=');disp(p);
disp('k=');disp(k);

可得: H ( z ) = 10 1 − 2 z − 1 + − 10 1 − z − 1 H(z)=\frac{10}{1-2z^{-1}}+\frac{-10}{1-z^{-1}} H(z)=1−2z−110+1−z−1−10
- rpk模型与tf模型之间的转换
residuez()
将 H ( z ) = 2 1 − z − 1 − 1 1 − 0.5 z − 1 + 1 1 + 0.5 z − 1 H(z)=\frac{2}{1-z^{-1}}-\frac{1}{1-0.5z^{-1}}+\frac{1}{1+0.5z^{-1}} H(z)=1−z−12−1−0.5z−11+1+0.5z−11转化为极点留数模型
% 使用residuez()
clear;
r = [2 -1 1]';
p = [1 0.5 -0.5];
k = 0;[b,a] = residuez(r,p,k);
disp('b=');disp(b);
disp('a=');disp(a);

可得: H ( z ) = 2 − z − 1 + 0.5 z − 2 1 − z − 1 − 0.25 z − 2 + 0.25 z − 3 H(z)=\frac{2-z^{-1}+0.5z^{-2}}{1-z^{-1}-0.25z^{-2}+0.25z^{-3}} H(z)=1−z−1−0.25z−2+0.25z−32−z−1+0.5z−2
- tf模型与ss模型之间的转换
tf2ss()
将 H ( z ) = 1.9 + 2.5 z − 1 + 2.5 z − 2 + 1.9 z − 3 1 − 6 z − 1 + 5 z − 2 − 0.4 z − 3 H(z)=\frac{1.9+2.5z^{-1}+2.5z^{-2}+1.9z^{-3}}{1-6z^{-1}+5z^{-2}-0.4z^{-3}} H(z)=1−6z−1+5z−2−0.4z−31.9+2.5z−1+2.5z−2+1.9z−3转化为状态变量模型
clear;b = [1.9 2.5 2.5 1.9];
a = [1 -6 5 -0.4];[A,B,C,D] = tf2ss(b,a);
disp('A=');disp(A);
disp('B=');disp(B);
disp('C=');disp(C);
disp('D=');disp(D);