写在前面

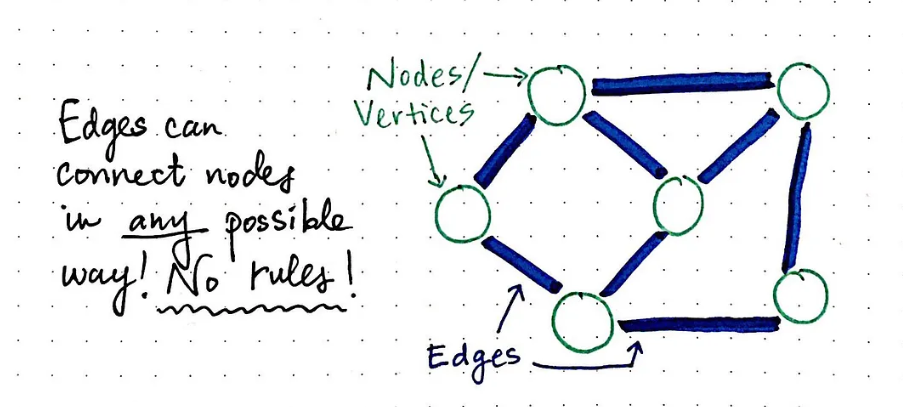
感知机、全连接层、神经网络是什么意思？

感知机： 是最简单的神经网络结构，可以对线性可分的数据进行分类。

全连接层： 是神经网络中的一种层结构，每个神经元与上一层的所有神经元相连接,实现全连接。

神经网络： 是由大量神经元组成的网络结构，通过层与层之间的连接，实现对数据的表示和转换。神经网络通常由输入层、隐藏层和输出层等全连接层构成。

三者有什么关系？

感知机是最简单的单层神经网络,仅有输入层和输出层。
全连接层是构建多层神经网络时常用的一种层类型。
神经网络通常由多层的全连接层叠加构成,从而实现比单层感知机更强大的功能。

所以可以说,感知机是简单的神经网络,全连接层是构建复杂神经网络的基础模块,神经网络通过组合多层全连接层实现复杂的功能。感知机和全连接层都是神经网络的组成要素。

写在中间

一、感知机

感知机（Perceptron）是一种简单的人工神经网络，由Frank Rosenblatt于1957年提出。它是一种线性二分类模型，主要用于解决二元分类问题。感知机的基本结构包括输入层、输出层和一个线性分类器。输入层接收输入数据，输出层提供分类结果，线性分类器将输入数据映射到输出层。

感知机模型的结构如下，它接受长度为𝑛的一维向量𝒙 = [𝑥1, 𝑥2, … , 𝑥𝑛]，每个输入节点通过权值为[w1, w2, … , w𝑛]的连接汇集为变量 𝑧

$z=w_{1}x_{1}+w_{2}x_{2}+\cdots+w_{n}x_{n}+b$

写为向量的形式为：

$z=w^{\mathrm{T}}x+b$

其中𝑏称为感知机的偏置(Bias)，一维向量𝒘 = [𝑤1, 𝑤2, … , 𝑤𝑛]称为感知机的权值(Weight)，𝑧 称为感知机的净活性值(Net Activation)。

感知机是线性模型，并不能处理线性不可分问题。通过在线性模型后添加激活函数后得到活性值(Activation) :

$a=\sigma(z)=\sigma(w^{\mathrm{T}}x+b)$

其中激活函数可以是阶跃函数，也可以是符号函数：

$a=\left\{\begin{matrix}1&w^\mathrm{T}x+b\geq0\\0&w^\mathrm{T}x+b<0\end{matrix}\right.$

$a=\left\{\begin{matrix}1&\text{w}^\mathrm{T}x+b\geq0\\-1&\text{w}^\mathrm{T}x+b<0\end{matrix}\right.$

在这里插入图片描述

二、全连接层

（ 1 ）了解概念

全连接层（Fully Connected Layer）是神经网络中的一种层结构，主要用于将前一层的输出与后一层的输入进行连接。全连接层中的每个神经元都与前一层的所有神经元相连，因此得名。它在感知机的基础上，将不连续的阶跃激活函数换成了其它平滑连续可导的激活函数，并通过堆叠多个网络层来增强网络的表达能力

我们通过替换感知机的激活函数，同时并行堆叠多个神经元来实现多输入、多输出的网络层结构。举一个最常用的例子：

构成 3 输入节点、2 个输出节点的网络层。其中第一个输出节点的输出为：

$o_1=\sigma(w_{11}\cdot x_1+w_{21}\cdot x_2+w_{31}\cdot x_3+b_1)$

第二个输出节点的输出为：

$o_{2}=\sigma(w_{12}\cdot x_{1}+w_{22}\cdot x_{2}+w_{32}\cdot x_{3}+b_{2})$

输出向量为𝒐 = [𝑜1, 𝑜2]，通过矩阵可以表达为如下的形式：

$\begin{bmatrix}o_1&o_2\end{bmatrix}=\begin{bmatrix}x_1&x_2&x_3\end{bmatrix}@\begin{bmatrix}w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\end{bmatrix}+\begin{bmatrix}b_1&b_2\end{bmatrix}$

可以归纳为

$\boldsymbol{O}=X@W+\boldsymbol{b}$

输入矩阵𝑿的 shape 定义为 $b, d_{in}]$ ，𝑏为样本数量，此处只有 1 个样本参与前向运算， $d_{in}$ 为输入节点数；权值矩阵 W 的 shape 定义为 $d_{in}, d_{out}]$ ， $d_{out}$ 为输出节点数，偏置向量 b 的 shape 定义为 $d_{out}]$ 。

（ 2 ）学会实现

全连接层本质上是矩阵的相乘和相加运算，实现并不复杂。TensorFlow 中有使用方便的层实现方式：layers.Dense(units, activation)。通过 layer.Dense 类，只需要指定输出节点数 units 和激活函数类型 activation 即可。

fc = layers.Dense(units=512, activation=tf.nn.relu)

上述通过一行代码即可以创建一层全连接层 fc，并指定输出节点数为 512，并创建内部权值张量𝑾和偏置张量𝒃。我们可以通过类内部的成员名 fc.kernel和 fc.bias来获取权值张量𝑾和偏置张量𝒃对象

三、神经网络

通过层层堆叠上面的全连接层，保证前一层的输出节点数与当前层的输入节点数匹配，，即可堆叠出任意层数的网络。我们把这种由神经元相互连接而成的网络叫做神经网络。

如图其中第 1~3 个全连接层在网络中间，称之为隐藏层 1、2、3，最后一个全连接层的输出作为网络的输出，称为输出层。隐藏层 1、2、3 的输出节点数分别为[256,128,64]，输出层的输出节点数为 10。

在这里插入图片描述

下面我们就用张量的方式来实现上面的神经网络

# 隐藏层 1 张量 
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1)) 
b1 = tf.Variable(tf.zeros([256])) 
# 隐藏层 2 张量 
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1)) 
b2 = tf.Variable(tf.zeros([128])) 
# 隐藏层 3 张量 
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1)) 
b3 = tf.Variable(tf.zeros([64])) 
# 输出层张量 
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1)) 
b4 = tf.Variable(tf.zeros([10]))

但是随着网络层数的增加，这样手动创建一个神经网络就显得过于繁琐，我们有更为简单的层实现方式，对于这种数据依次向前传播的网络，也可以通过 Sequential 容器封装成一个网络大类对象，调用大类的前向计算函数一次即可完成所有层的前向计算，使用起来更加方便：

#  导入 Sequential 容器 
from keras import layers,Sequential #  通过 Sequential 容器封装为一个网络类 
model = Sequential([ layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1 layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2  layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3  layers.Dense(10, activation=None) , # 创建输出层  
])  out = model(x) #  前向计算得到输出

至此，网络构建的大体流程就讲解完毕了