友塔游戏测试开发笔面经验-编程知识

题目一

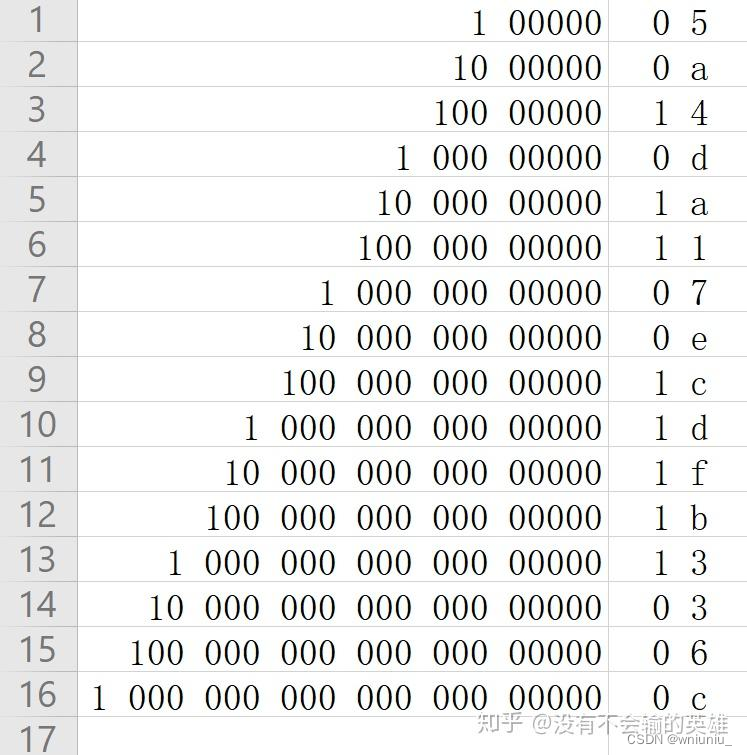
给定任意非负整数M，判断其能否表达为 M = 2 ^a + 2 ^b(a和b为非负整数)，若可以输出a和b，若不能输出-1；

例如：输入：6 输出: “1 2”

分析：

void findAB(int M){} 为解决问题的主函数

流程：

若 M <= 0, 2的幂次无法为0，故认为无解，直接返回 “-1”
检查M是否是2的幂次方，如果是，直接输出 “0 log2(M)”
用两层循环遍历所有可能得a值和b值查找可能得结果，检查的范围限定在 a 在 [0, log2M]， b 在 [a + 1, log2M]， b 从 a+ 1开始是为了避免重复， a 和 b 相同且为结果在

第二步就能求出，即 $ 2 ^a + 2^a = 2^(a+1) $

代码

// 函数用于判断一个数是否是2的幂次方
bool isPowerOfTwo(int n)
{// n 不能为0// 且n的二进制表示只有一个1， n & (n - 1) 将 n 最右边的1变为0return (n && !(n & (n - 1)));
}string findAB(int M)
{if(M <= 0){return "-1";}// 检查M是否是2的幂次方，如果是，直接输出if(isPowerOfTwo(M)){return "0 " + to_string((int)log2(M));}for(int a = 0; a <= log2(M); ++a){for(int b = a + 1; b <= log2(M); ++b)  // b从a+1开始，避免重复{if(pow(2, a) + pow(2, b) == M){return to_string(a) + " " + to_string(b);}}}return "-1";
}

题目二

圆上按顺序有编号1到n的n个点。两点间连线，连过线的点不与其他点相连。要求这些线都不相交，n为偶数时最终有 n/2条线，n为奇数时有 (n - 1) / 2条线，输入点的个数n，输出满足要求的方法数量。

例如：

输入：4

输出: 2

函数原型为 int solution(int n)

分析

对于给定的n个点（n为偶数），以这些点为端点连互不相交的弦的方法数量就是第n/2个卡塔兰数。

卡塔兰数的递推公式为

在这里插入图片描述

对于n个点连接不相交弦的问题，由于每条弦都会将圆分成两部分，每一部分内的弦也必须满足不相交的条件，因此问题可以递归地分解成更小的子问题，这正好对应卡塔兰数的定义。

但是n为奇数的时候，要保证所有连线不相交，则相交线数量为 (n - 1) / 2 ,且必然有一个点没被连接，所以可以任取一个点作为没被连接的点，从而得不相交弦的方法数量为：
n*C((n - 1) / 2)

unsigned long long catalan(unsigned int n)
{if(n <= 1) return 1;vector<unsigned long long> C(n + 1, 0);C[0] = C[1] = 1;// 递推式的循环表示for(unsigned int i = 2; i <= n; ++i){for(unsigned int j = 0; j < i; ++j){C[i] += C[j] * C[i - j - 1];}}return C[n];
}// 核心主函数
unsigned long long chordCount(int n)
{if(n % 2 != 0){// 奇数的情况return n * catalan((n - 1) / 2);}else{return catalan(n / 2);}
}

解法二

int solution(int n) {// 卡特兰数通常用于解决此类问题// dp数组用于存储结果，dp[i]表示i个点形成非交叉连线的方法数vector<int> dp(n + 1, 0);dp[0] = 1; // 没有点时认为有一种方法dp[2] = 1; // 两个点只有一种连接方式// 填充dp数组for (int i = 4; i <= n; i += 2) { // 只考虑偶数个点，因为奇数个点不可能完全配对for (int j = 0; j < i - 1; j += 2) {// dp[i]累加上dp[j]（左侧的点形成的配对方式）* dp[i - j - 2]（右侧的点形成的配对方式）dp[i] += dp[j] * dp[i - j - 2];}}return (n % 2) ? (n * dp[n - 1]) : dp[n];
}

题目三

小游戏是一个正八边形，每条边有打开(1),关闭(0)两种状态，每次执行游戏选定一条边，把该边和其相邻的两条边（共三条）改为格子相反的状态。如三边为1 0 1，选定中间边进行一次操作结果为 0 1 0 。输入一个一维数组M（数字0或1）表示八条边的初始状态，输出最少需要多少次可以把八条边都置位0。

例如：

输入：[0, 0, 0, 0, 0, 0, 0, 1]

输出 : 5

函数原型为int solution(vector<int> M)

分析

解决该问题的方法是如何通过有限的操作将八边形的每条边都转为0状态。由于问题规模较小，可用位运算和穷举来寻找最优解。

每一条边的状态可以用一个8位的二进制数表示，每位代表一条边的开或关状态。因此，可以通过【遍历所有可能的操作序列】来找到将所有边都转换为0状态的最小操作次数。

使用双层循环来遍历每一种翻转的情况：

for (int seq = 0; seq < (1 << 8); ++seq) {

这个循环遍历所有可能的操作序列。seq变量代表当前的操作序列，用一个8位的二进制数表示，其中每一位对应于八边形的一条边是否被选择进行操作。所以一共 2^8种情况。

内层循环如下：

for (int j = 0; j < 8; ++j) {if (seq & (1 << j)) {state = flip(state, j);steps++;}}

这个循环遍历当前操作序列seq的每一位，检查每一条边是否被选择进行操作。

seq & (1 << j)是位操作，检查seq的第j位是否为1。如果结果非0，意味着在当前操作序列中，第j条边被选中进行操作。

如果第j条边被选中，那么调用 flip(state, j) 函数翻转第j条边及其相邻两条边的状态。state变量代表当前的边状态，是一个8位的二进制数，每一位对应一条边的开或关状态。

steps++记录了进行当前序列操作所需的步数。

最后进行检查和更新最少操作次数

if (state == 0) {minOperations = min(minOperations, steps);}

代码

int flip(int state, int index)
{// 翻转当前位state ^= 1 << index;state ^= 1 << ((index + 7) % 8);state ^= 1 << ((index + 1) % 8);return state;
}int solution(vector<int> M)
{int initialState = 0;for(int i = 0; i < 8; ++i){initialState |= M[i] << i; // 初始化状态}int minOperations = INT_MAX;// 尝试所有可能的操作序列，见分析// 如seq = 3 = 0000 0011 , 即代表最前面两位进行翻转操作，其余不动for(int seq = 0; seq < (1 << 8); ++seq){int state = initialState;int steps = 0;for(int j = 0; j < 8; ++j){if(seq & (1 << j)) // 检查第j位是否为1， 若是，则翻转{state = flip(state, j);steps++;}}if(state == 0){minOperations = min(minOperations, steps);}}return minOperations == INT_MAX ? -1 : minOperations;
}