插入排序:一种简单而有效的排序算法
- 一、什么是插入排序?
- 二、插入排序的步骤
- 三、插入排序的C语言实现
- 四、插入排序的性能分析
- 五、插入排序的优化
- 六、总结
在我们日常生活和工作中,排序是一种非常常见的操作。比如,我们可能需要对一堆无序的文件、一组杂乱的数据或者一堆扑克牌进行排序。在计算机科学中,排序同样是一个核心问题,而插入排序就是解决这一问题的一种基础而有效的方法。
一、什么是插入排序?
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
具体来说,插入排序的工作方式就像我们许多人排序一手扑克牌。开始时,我们的左手为空并且桌子上的牌面向下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的,原来这些牌是桌子上牌堆中顶部的牌。
二、插入排序的步骤
插入排序的基本操作是将一个数据元素插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。
插入排序的步骤如下:
从第一个元素开始,该元素可以认为已经被排序;
取出下一个元素,在已经排序的元素序列中从后向前扫描;
如果该元素(已排序)大于新元素,将该元素移到下一位置;
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
将新元素插入到该位置后;
重复步骤2~5。

三、插入排序的C语言实现
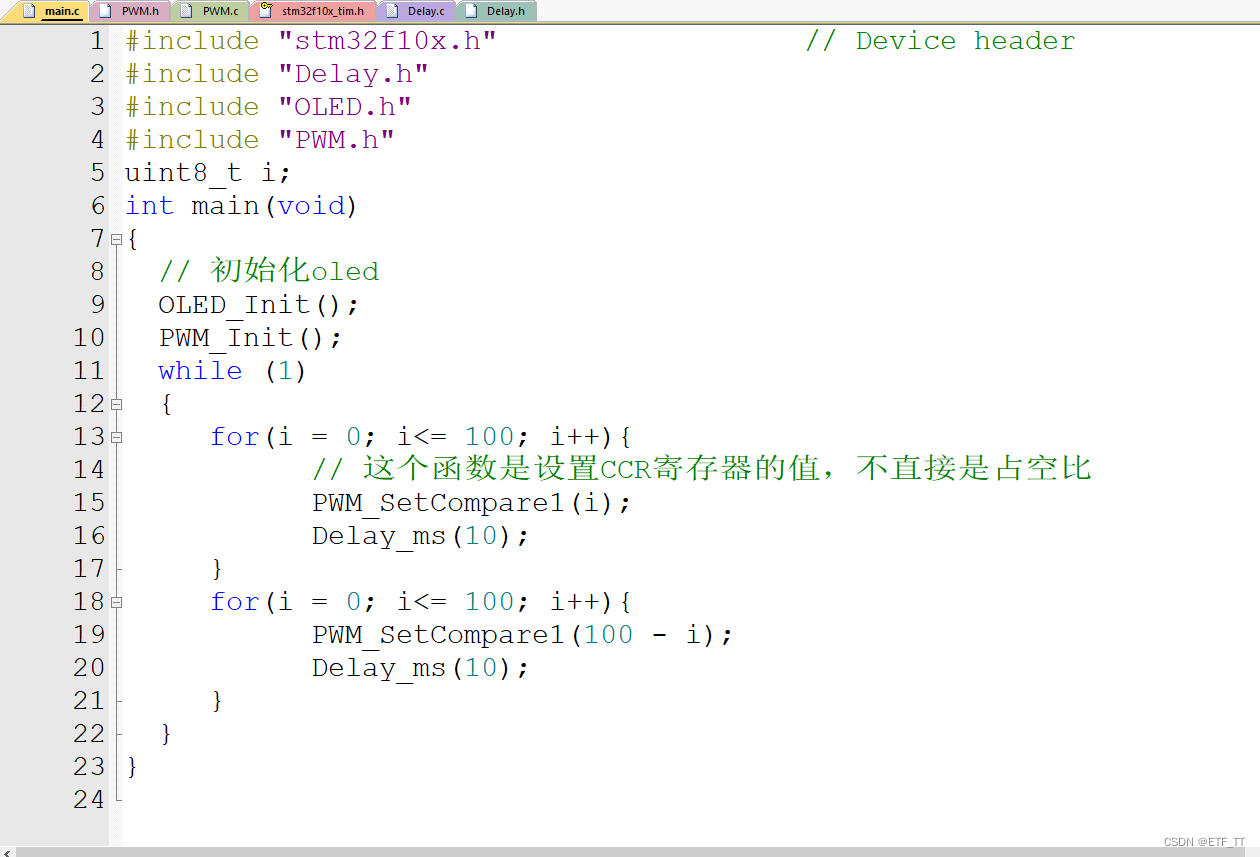
下面是一个简单的插入排序的C语言实现:
c
#include <stdio.h> void insertionSort(int arr[], int n) { int i, key, j; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; /* Move elements of arr[0..i-1], that are greater than key, to one position ahead of their current position */ while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; }
} /* A utility function to print array of size n */
void printArray(int arr[], int n) { int i; for (i = 0; i < n; i++) printf("%d ", arr[i]); printf("\n");
} /* Test the above functions */
int main() { int arr[] = {12, 11, 13, 5, 6}; int n = sizeof(arr) / sizeof(arr[0]); insertionSort(arr, n); printf("Sorted array: \n"); printArray(arr, n); return 0;
}
在这个例子中,我们首先定义了一个insertionSort函数,它接受一个整数数组arr和数组的长度n作为参数。然后,我们使用一个for循环来遍历数组中的每个元素。对于每个元素,我们将其保存在变量key中,并将j初始化为当前元素的索引减一。然后,我们使用一个while循环来将大于key的元素向后移动一位,直到找到key的正确位置。最后,我们将key插入到正确的位置。
在main函数中,我们定义了一个需要排序的数组arr,并计算了数组的长度n。然后,我们调用insertionSort函数对数组进行排序,并使用printArray函数打印排序后的数组。
四、插入排序的性能分析
插入排序的时间复杂度是O(n2),其中n是待排序元素的数量。在最坏的情况下,即输入序列是逆序的情况下,每次插入都需要移动大量的元素,因此时间复杂度达到O(n2)。然而,在最好的情况下,即输入序列已经是有序的情况下,插入排序的时间复杂度可以降低到O(n)。这是因为在这种情况下,每次插入操作都不需要移动任何元素。
尽管插入排序的时间复杂度相对较高,但它在实际应用中仍然有其价值。特别是当待排序的数据量较小,或者数据部分有序时,插入排序可能比其他更复杂的排序算法更有效。此外,插入排序是一种稳定的排序算法,即相等的元素的顺序在排序后不会改变。这对于某些需要保持相等元素相对顺序的应用场景来说是非常重要的。
五、插入排序的优化
虽然插入排序的基本形式在大多数情况下的性能并不是最优的,但可以通过一些优化手段来提高其效率。
二分插入排序:在基本插入排序中,我们逐个比较和移动元素。而在二分插入排序中,我们使用二分查找来确定新元素应该插入的位置,从而减少比较次数。但是,元素移动的次数仍然是相同的。
希尔排序:也被称为缩小增量排序,是插入排序的一种高效版本。希尔排序首先比较较远的元素,然后逐步减小排序的间隔。当间隔为1时,算法就变成了普通的插入排序。通过这种方式,希尔排序能够在早期阶段消除大量的无序情况,使得后续的插入排序更加高效。
六、总结
插入排序是一种简单直观的排序算法,它通过将未排序的元素插入到已排序的序列中来逐步构建有序序列。虽然它的时间复杂度在最坏情况下是O(n^2),但在数据量较小或数据部分有序时,插入排序可以表现得相当不错。此外,插入排序是稳定的,能够保持相等元素的相对顺序。
通过了解插入排序的工作原理和实现方式,我们可以更好地理解排序算法的基础,并为学习更复杂的排序算法打下坚实的基础。在实际应用中,我们可以根据具体的数据特性和需求来选择合适的排序算法,以达到最优的排序效果。



![中间件 | RPC - [Dubbo]](https://img-blog.csdnimg.cn/direct/f2296201d2604c08aea759d34b456e9a.png)