原题
题目描述
在大学期间,经常需要租借教室。
大到院系举办活动,小到学习小组自习讨论,都需要向学校申请借教室。
教室的大小功能不同,借教室人的身份不同,借教室的手续也不一样。
面对海量租借教室的信息,我们自然希望编程解决这个问题。
我们需要处理接下来 n 天的借教室信息,其中第 i 天学校有 ri 个教室可供租借。
共有 m 份订单,每份订单用三个正整数描述,分别为 dj,sj,tj 表示某租借者需要从第 sj 天到第 tj 天租借教室(包括第 sj 天和第 tj 天),每天需要租借 dj 个教室。
我们假定,租借者对教室的大小、地点没有要求。
即对于每份订单,我们只需要每天提供 dj 个教室,而它们具体是哪些教室,每天是否是相同的教室则不用考虑。
借教室的原则是先到先得,也就是说我们要按照订单的先后顺序依次为每份订单分配教室。
如果在分配的过程中遇到一份订单无法完全满足,则需要停止教室的分配,通知当前申请人修改订单。
这里的无法满足指从第 sj 天到第 tj 天中有至少一天剩余的教室数量不足 dj 个。
现在我们需要知道,是否会有订单无法完全满足。
如果有,需要通知哪一个申请人修改订单。
输入格式
第一行包含两个正整数 n,m 表示天数和订单的数量。
第二行包含 n个正整数,其中第 i 个数为 ri 表示第 i 天可用于租借的教室数量。
接下来有 m行,每行包含三个正整数 dj,sj,tj 表示租借的数量,租借开始、结束分别在第几天。
每行相邻的两个数之间均用一个空格隔开。
天数与订单均用从 1 开始的整数编号。
输出格式
如果所有订单均可满足,则输出只有一行,包含一个整数 00。
否则(订单无法完全满足)输出两行,第一行输出一个负整数 −1−1,第二行输出需要修改订单的申请人编号。
数据范围
1≤n,m≤106,
0≤ri,dj≤109,
1≤sj≤tj≤n
输入样例:
4 3
2 5 4 3
2 1 3
3 2 4
4 2 4
输出样例:
-1
2思路:
借教室的订单,其实就是在每天需要教室数量的数组上进行一个区间的增减,可以用差分数组快速得到区间的变化,而又因为订单满足先来后到,即如果要处理第k个订单,必须保证从1到k-1号订单全部可以满足,那么就可以知道存在一个分界线:有最后一个能处理的订单x,在它之后的所有订单都不能处理,在它之前的所有订单都可以满足。那么就可以用二分去做。
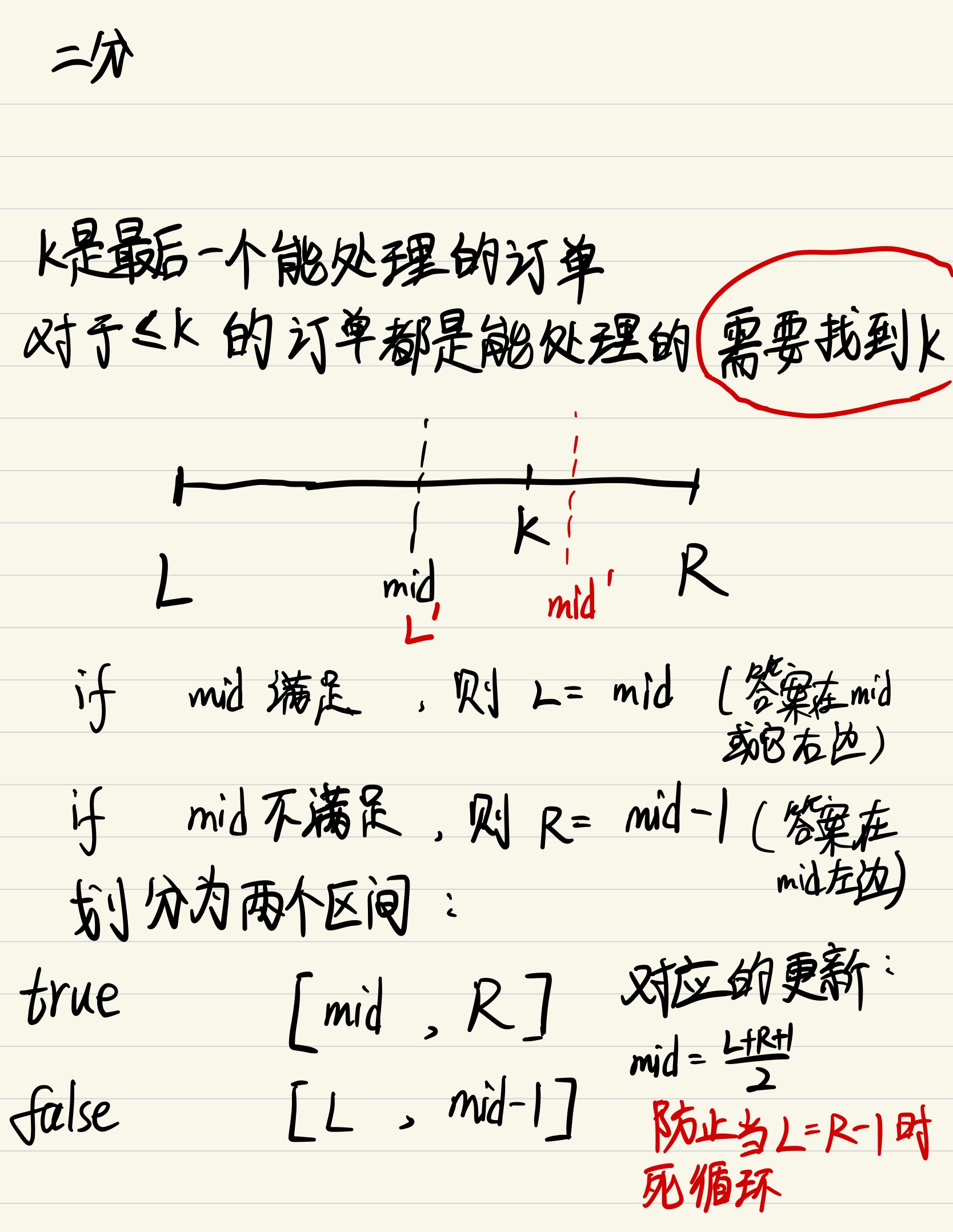

差分数组:


bi是di相对于di-1的差值,通过差值我们也能计算出订单的需要教室数。如果有变化,就会在差分数组最左端+di,最右+1的位置-di,这就得到了教室数。
比如b1+2,b4-2,默认d0=0,那么d1相对d0多2,d1到d3不变,d4相对d3少2。
那么我们很容易得到结果,d0=0,d1~d3=2,d4=0,即在d1到d3这几天,我们每天都需要2个教室
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>using namespace std;typedef long long LL;const int N=1e6+10;int n,m;
int w[N]; //第i天有wi个教室可供租借
int d[N],s[N],t[N];
LL b[N]; //差分数组bool check(int mid)
{memset(b,0,sizeof b); //每次检查,差分数组置零,防止上次操作影响//为什么这里不用计算差分数组初始值:b[i]=d[i]-d[i-1]? 注意,我们计算的是从1到mid的差分数组,mid每次都会变,如果不置零会导致上一次的差分数组影响这次的计算//bi是di相对于di-1的差值,通过差值我们也能计算出订单的需要教室数//如果有变化,就会在差分数组最左端+di,最右+1的位置-di,这就得到了教室数//比如b1+2,b4-2,默认d0=0,那么d1相对d0多2,d1到d3不变,d4相对d3少2//那么我们很容易得到结果,d0=0,d1~d3=2,d4=0,即在d1到d3这几天,我们每天都需要2个教室for(int i=1;i<=mid;i++) //从1号到mid号订单,用差分数组记录每天租借教室数量di{//si,ti表示第i份订单租借开始、结束的天数b[s[i]]+=d[i];b[t[i]+1]-=d[i]; //差分数组b,记录变化}LL s=0; //for(int i=1;i<=n;i++){s+=b[i]; //s相当于原数组,差分数组相加就是第i天需要的教室数量//如果有一天需要的教室比能提供的多,就不行if(s>w[i]) return false;}return true;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&w[i]);}for(int i=1;i<=m;i++){scanf("%d%d%d",&d[i],&s[i],&t[i]);}//二分,共有m份订单,找到最后一个能处理的订单int l=0,r=m; //从0开始,有可能一个订单都不能满足while(l<r){int mid=l+r+1 >> 1; //取中点,这里+1是模板需要if(check(mid)) l=mid;else r=mid-1;}if(r==m) puts("0"); //所有订单都可以满足else printf("-1\n%d\n",r+1); //如果不能满足,输出第一个不能满足的编号} 为什么这里的代码不需要初始化差分数组:
for(int i=1;i<=mid;i++){b[i]=d[i]-d[i-1];}因为题目中初始情况下,每一天所需的教室数都为0,所需的教室数量是根据后面的订单才发生变化的,也就是说,要计算教室数量,就可以通过订单(差分数组)来计算,这些得到的差值加起来就是某天所需要的教室数量。
为什么L要从0开始?
int l=0,r=m; //从0开始,有可能一个订单都不能满足while(l<r){int mid=l+r+1 >> 1; //取中点,这里+1是模板需要if(check(mid)) l=mid;else r=mid-1;}if(r==m) puts("0"); //所有订单都可以满足else printf("-1\n%d\n",r+1); //如果不能满足,输出第一个不能满足的编号当n和m都为1,且这一天都不能满足,正确答案应该是-1 1
但若从1开始,则不会进入while循环,直接输出0
若从0开始,则会将r变为0,输出-1 0+1
差分
再看一道经典差分题,也可以用上面的【差分数组是原数组相邻元素的差值】来解:
题目描述
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n和 m。
第二行包含 n个整数,表示整数序列。
接下来 m行,每行包含三个整数 l,r,c表示一个操作。
输出格式
共一行,包含 n个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2原解法:
#include<iostream>
using namespace std;
int m,n;
typedef long long ll;
const int N=1e5+10;
int a[N];
int diff[N]; int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){diff[i]=a[i]-a[i-1]; //差分初始化}while(m--){int c,l,r;cin>>l>>r>>c;diff[l]+=c;diff[r+1]-=c; //这里是自增自减,记得+=,-= }for(int i=1;i<=n;i++){a[i]=diff[i]+a[i-1];} //记得最后还原成原数组,这样才能作用到原数组上面for(int i=1;i<=n;i++){cout<<a[i]<<" ";}return 0;
}新解法:
#include<iostream>
#include<cstring>
using namespace std;
int m,n;
typedef long long ll;
const int N=1e5+10;
int a[N];
int diff[N]; int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){diff[i]=a[i]-a[i-1]; //差分初始化,因为这个本身就有给整数序列,所以需要计算,而借教室那道题,本身所需教室为0,是通过一个一个订单计算得到的,所以不需要计算初始值}while(m--){int c,l,r;cin>>l>>r>>c;diff[l]+=c;diff[r+1]-=c; //这里是自增自减,记得+=,-= }int s=0;for(int i=1;i<=n;i++){//不同之处:这次我们直接通过差值来计算s+=diff[i];cout<<s<<" ";} return 0;
}这道题和借教室的不同就在于:差分初始化,因为这个题目本身就有给整数序列(即原来的a是有初始值的),所以需要计算差分数组的初始值,而借教室那道题,本身所需教室为0,是通过一个一个订单计算得到的,所以不需要计算初始值