两道最短路好题

POJ3037

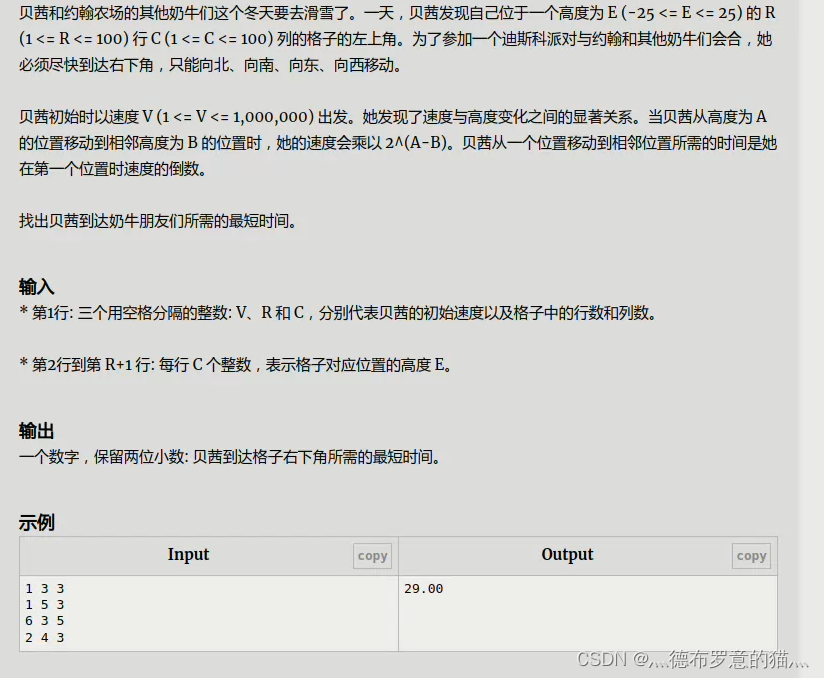
手玩一下 发现每一点的速度可以直接搞出来，就是pow(2,h[1][1]-h[i][j])*V

那么从这个点出发到达别的点的耗费的时间都是上面这个数的倒数，然后直接跑最短路就好了

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;const int N = 1e5+10;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
int gcd(int a,int b){return b?a:gcd(b,a%b);}
int lcm(int a,int b){return a*b/gcd(a,b);}
int qmi(int a,int b,int mod){int res=1;while(b){if(b&1)res=res*a%mod;b>>=1;a=a*a%mod;}return res;}int n,q,m,v;
bool vis[1010][1010];
// int e[N],ne[N],w[N],h[N],idx;
// void add(int a,int b,int c){// e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
// }double vs[1010][1010];
double dist[1010][1010];
double h[1010][1010];void solve()
{cin>>v>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){double x;cin>>x;h[i][j] = x;vs[i][j] = pow(2,x-h[1][1])/v; dist[i][j] = 1e15;}}dist[1][1] = 0;queue<pair<int,int>>q;q.push(make_pair(1,1));int dx[] = {0,0,1,-1};int dy[] = {1,-1,0,0};vis[1][1] = true;while(q.size()){pair<int,int> t = q.front();q.pop();int x = t.first,y = t.second;vis[x][y] = false;//cout<<x<<" "<<y<<"\n";for(int i=0;i<4;i++){int temx = x+dx[i],temy = y+dy[i];if(temx<1||temx>n||temy<1||temy>m)continue;//cout<<temx<<" "<<temy<<"\n";if(dist[temx][temy]>dist[x][y]+vs[x][y]){dist[temx][temy] = dist[x][y]+vs[x][y];if(!vis[temx][temy]){vis[temx][temy] = true;q.push(make_pair(temx,temy));}}}}printf("%.2lf",dist[n][m]);}signed main()
{//ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _;//cin>>_;_ = 1;while(_--)solve();return 0;
}

HDU6714

这个dijk记数还是很有意思的，你得明白folyd的含义但是别被DP的含义绕进去

每次暴力的跑每一个点的单源最短路，然后当有中间点的时候你就更新一下就行了，没有中间的时候D【i】【j】就是一开始的距离，没有被更新，还是很有趣的，还是得想明白floyd的具体过程（好像不懂也行

一开始我就被绕进去了，一直在扣floyd 的含义来写这道，发现直接按上面的做法就好了

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define int long long
using pii = pair<int,int>;
const int N = 1e4+10;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
int gcd(int a,int b){return b?a:gcd(b,a%b);}
int lcm(int a,int b){return a*b/gcd(a,b);}
int qmi(int a,int b,int mod){int res=1;while(b){if(b&1)res=res*a%mod;b>>=1;a=a*a%mod;}return res;}int n,q,m;
int id[N];
int e[N],ne[N],w[N],h[N],idx;
void add(int a,int b,int c){e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
}bool vis[N];
ll dist[N];void dijkstra(int mid)
{memset(dist,0x3f,sizeof dist);memset(vis,0,sizeof vis);memset(id,0,sizeof id);priority_queue<pii,vector<pii>,greater<pii>>heap;heap.push({0,mid});dist[mid] = 0;while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second;if(vis[ver])continue;vis[ver] = true;//cout<<ver<<"\n";for(int i=h[ver];~i;i=ne[i]){int j = e[i];if(dist[j]>dist[ver]+w[i]){dist[j] = dist[ver]+w[i];heap.push({dist[j],j});if(ver==mid)continue;id[j] = max(id[ver],ver);}else if(dist[j]==dist[ver]+w[i]){id[j] = min(id[j],max(id[ver],ver));}}}
}void solve()
{cin>>n>>m;memset(h,-1,sizeof h);idx = 0;while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c),add(b,a,c);}int ans = 0;for(int i=1;i<=n;i++){dijkstra(i);for(int j=1;j<=n;j++)ans = (id[j]+ans)%mod;//cout<<"\n";}cout<<ans;}signed main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _;cin>>_;//_ = 1;while(_--)solve();return 0;
}