一元函数:
一、极限存在的条件
二、连续的条件
三、可导的条件
四、可微的条件
五、原函数存在的条件
目录
一、极限存在的条件
1.自变量趋于无穷大时函数的极限
2.自变量趋于有限值时函数的极限
二、连续的条件
1.自变量改变量趋于0时,函数值改变量也趋于0
2.该点的极限等于该点的函数值
3.在该点既左连续又右连续
三、可导的条件
四、可微的条件
五、原函数存在的条件
一、极限存在的条件
1.自变量趋于无穷大时函数的极限
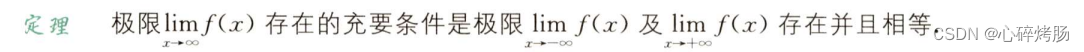
2.自变量趋于有限值时函数的极限
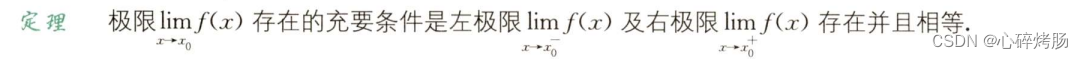
二、连续的条件
1.自变量改变量趋于0时,函数值改变量也趋于0

2.该点的极限等于该点的函数值

3.在该点既左连续又右连续

三、可导的条件

四、可微的条件

注意:可微一定可导,可导一定可微。这个定理只适用于一元函数,多元函数并不适用;
五、原函数存在的条件


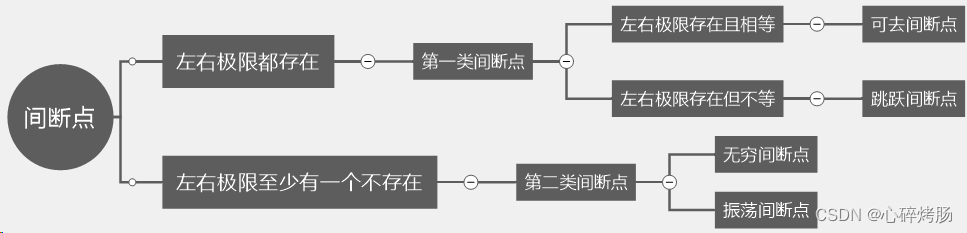
补充:第一类间断点