用echarts实现进度条-编程知识

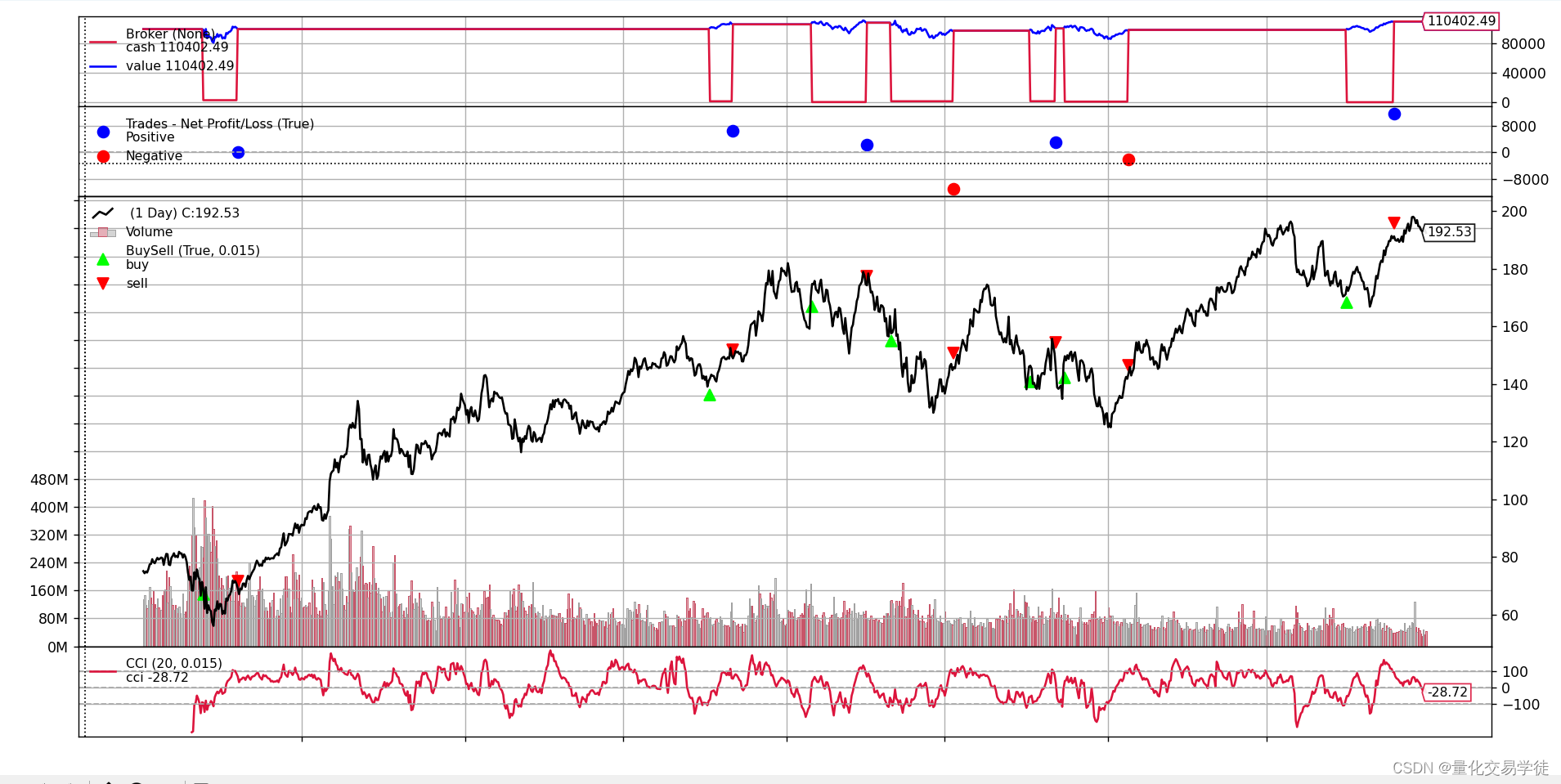
今天有个需求需要实现类似这种进度条在这里插入图片描述
渐变，指示点，背景这些都比较容易实现，前面这段有个高度逐渐增大的地方卡住了，半天没想到用什么方式去实现，搜了一圈，发现可以用echarts来实现


let icon1 = 'image://data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADwAAAA8CAYAAAA6/NlyAAAABGdBTUEAALGPC/xhBQAACklpQ0NQc1JHQiBJRUM2MTk2Ni0yLjEAAEiJnVN3WJP3Fj7f92UPVkLY8LGXbIEAIiOsCMgQWaIQkgBhhBASQMWFiApWFBURnEhVxILVCkidiOKgKLhnQYqIWotVXDjuH9yntX167+3t+9f7vOec5/zOec8PgBESJpHmomoAOVKFPDrYH49PSMTJvYACFUjgBCAQ5svCZwXFAADwA3l4fnSwP/wBr28AAgBw1S4kEsfh/4O6UCZXACCRAOAiEucLAZBSAMguVMgUAMgYALBTs2QKAJQAAGx5fEIiAKoNAOz0ST4FANipk9wXANiiHKkIAI0BAJkoRyQCQLsAYFWBUiwCwMIAoKxAIi4EwK4BgFm2MkcCgL0FAHaOWJAPQGAAgJlCLMwAIDgCAEMeE80DIEwDoDDSv+CpX3CFuEgBAMDLlc2XS9IzFLiV0Bp38vDg4iHiwmyxQmEXKRBmCeQinJebIxNI5wNMzgwAABr50cH+OD+Q5+bk4eZm52zv9MWi/mvwbyI+IfHf/ryMAgQAEE7P79pf5eXWA3DHAbB1v2upWwDaVgBo3/ldM9sJoFoK0Hr5i3k4/EAenqFQyDwdHAoLC+0lYqG9MOOLPv8z4W/gi372/EAe/tt68ABxmkCZrcCjg/1xYW52rlKO58sEQjFu9+cj/seFf/2OKdHiNLFcLBWK8ViJuFAiTcd5uVKRRCHJleIS6X8y8R+W/QmTdw0ArIZPwE62B7XLbMB+7gECiw5Y0nYAQH7zLYwaC5EAEGc0Mnn3AACTv/mPQCsBAM2XpOMAALzoGFyolBdMxggAAESggSqwQQcMwRSswA6cwR28wBcCYQZEQAwkwDwQQgbkgBwKoRiWQRlUwDrYBLWwAxqgEZrhELTBMTgN5+ASXIHrcBcGYBiewhi8hgkEQcgIE2EhOogRYo7YIs4IF5mOBCJhSDSSgKQg6YgUUSLFyHKkAqlCapFdSCPyLXIUOY1cQPqQ28ggMor8irxHMZSBslED1AJ1QLmoHxqKxqBz0XQ0D12AlqJr0Rq0Hj2AtqKn0UvodXQAfYqOY4DRMQ5mjNlhXIyHRWCJWBomxxZj5Vg1Vo81Yx1YN3YVG8CeYe8IJAKLgBPsCF6EEMJsgpCQR1hMWEOoJewjtBK6CFcJg4Qxwicik6hPtCV6EvnEeGI6sZBYRqwm7iEeIZ4lXicOE1+TSCQOyZLkTgohJZAySQtJa0jbSC2kU6Q+0hBpnEwm65Btyd7kCLKArCCXkbeQD5BPkvvJw+S3FDrFiOJMCaIkUqSUEko1ZT/lBKWfMkKZoKpRzame1AiqiDqfWkltoHZQL1OHqRM0dZolzZsWQ8ukLaPV0JppZ2n3aC/pdLoJ3YMeRZfQl9Jr6Afp5+mD9HcMDYYNg8dIYigZaxl7GacYtxkvmUymBdOXmchUMNcyG5lnmA+Yb1VYKvYqfBWRyhKVOpVWlX6V56pUVXNVP9V5qgtUq1UPq15WfaZGVbNQ46kJ1Bar1akdVbupNq7OUndSj1DPUV+jvl/9gvpjDbKGhUaghkijVGO3xhmNIRbGMmXxWELWclYD6yxrmE1iW7L57Ex2Bfsbdi97TFNDc6pmrGaRZp3mcc0BDsax4PA52ZxKziHODc57LQMtPy2x1mqtZq1+rTfaetq+2mLtcu0W7eva73VwnUCdLJ31Om0693UJuja6UbqFutt1z+o+02PreekJ9cr1Dund0Uf1bfSj9Rfq79bv0R83MDQINpAZbDE4Y/DMkGPoa5hpuNHwhOGoEctoupHEaKPRSaMnuCbuh2fjNXgXPmasbxxirDTeZdxrPGFiaTLbpMSkxeS+Kc2Ua5pmutG003TMzMgs3KzYrMnsjjnVnGueYb7ZvNv8jYWlRZzFSos2i8eW2pZ8ywWWTZb3rJhWPlZ5VvVW16xJ1lzrLOtt1ldsUBtXmwybOpvLtqitm63Edptt3xTiFI8p0in1U27aMez87ArsmuwG7Tn2YfYl9m32zx3MHBId1jt0O3xydHXMdmxwvOuk4TTDqcSpw+lXZxtnoXOd8zUXpkuQyxKXdpcXU22niqdun3rLleUa7rrStdP1o5u7m9yt2W3U3cw9xX2r+00umxvJXcM970H08PdY4nHM452nm6fC85DnL152Xlle+70eT7OcJp7WMG3I28Rb4L3Le2A6Pj1l+s7pAz7GPgKfep+Hvqa+It89viN+1n6Zfgf8nvs7+sv9j/i/4XnyFvFOBWABwQHlAb2BGoGzA2sDHwSZBKUHNQWNBbsGLww+FUIMCQ1ZH3KTb8AX8hv5YzPcZyya0RXKCJ0VWhv6MMwmTB7WEY6GzwjfEH5vpvlM6cy2CIjgR2yIuB9pGZkX+X0UKSoyqi7qUbRTdHF09yzWrORZ+2e9jvGPqYy5O9tqtnJ2Z6xqbFJsY+ybuIC4qriBeIf4RfGXEnQTJAntieTE2MQ9ieNzAudsmjOc5JpUlnRjruXcorkX5unOy553PFk1WZB8OIWYEpeyP+WDIEJQLxhP5aduTR0T8oSbhU9FvqKNolGxt7hKPJLmnVaV9jjdO31D+miGT0Z1xjMJT1IreZEZkrkj801WRNberM/ZcdktOZSclJyjUg1plrQr1zC3KLdPZisrkw3keeZtyhuTh8r35CP5c/PbFWyFTNGjtFKuUA4WTC+oK3hbGFt4uEi9SFrUM99m/ur5IwuCFny9kLBQuLCz2Lh4WfHgIr9FuxYji1MXdy4xXVK6ZHhp8NJ9y2jLspb9UOJYUlXyannc8o5Sg9KlpUMrglc0lamUycturvRauWMVYZVkVe9ql9VbVn8qF5VfrHCsqK74sEa45uJXTl/VfPV5bdra3kq3yu3rSOuk626s91m/r0q9akHV0IbwDa0b8Y3lG19tSt50oXpq9Y7NtM3KzQM1YTXtW8y2rNvyoTaj9nqdf13LVv2tq7e+2Sba1r/dd3vzDoMdFTve75TsvLUreFdrvUV99W7S7oLdjxpiG7q/5n7duEd3T8Wej3ulewf2Re/ranRvbNyvv7+yCW1SNo0eSDpw5ZuAb9qb7Zp3tXBaKg7CQeXBJ9+mfHvjUOihzsPcw83fmX+39QjrSHkr0jq/dawto22gPaG97+iMo50dXh1Hvrf/fu8x42N1xzWPV56gnSg98fnkgpPjp2Snnp1OPz3Umdx590z8mWtdUV29Z0PPnj8XdO5Mt1/3yfPe549d8Lxw9CL3Ytslt0utPa49R35w/eFIr1tv62X3y+1XPK509E3rO9Hv03/6asDVc9f41y5dn3m978bsG7duJt0cuCW69fh29u0XdwruTNxdeo94r/y+2v3qB/oP6n+0/rFlwG3g+GDAYM/DWQ/vDgmHnv6U/9OH4dJHzEfVI0YjjY+dHx8bDRq98mTOk+GnsqcTz8p+Vv9563Or59/94vtLz1j82PAL+YvPv655qfNy76uprzrHI8cfvM55PfGm/K3O233vuO+638e9H5ko/ED+UPPR+mPHp9BP9z7nfP78L/eE8/stRzjPAAAAIGNIUk0AAHomAACAhAAA+gAAAIDoAAB1MAAA6mAAADqYAAAXcJy6UTwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAipSURBVGiB5ZttcFTVGcd/ezcJu3lpElgrAYQklJIXkmqhDLUMYINYHTpOP9Wplr7MfizasdLqFmdsdbYobadqP+5UxGmdfuyM5aUwNCp2sBbEvBMkibYQaFeTmGR3CcluPzx3YXdzz73nZjeRGf8zmcmce+55nv+ec57nOc95rieVSvFZgvFpK7DQKEr/c3tn6XyMHwA2AGuAlcAqoBqoMGVPA+PACPAB8CFwHvgXEC20MmdbYjcIFxC1wE5gK0L4XaAbOIoQigITwBRQApQDi4HlQB2wA/iZ2e914DVgqFDKedJ7OM8ZNoBtwPeBWxFyR4FeIDnH8RqBe8y/K8ABoH2O4wEyw4UgvAX4ETJjf8hXKQsYpoxdyGr4PfDGXAbKd0kvAx5DlvBvgZN5jGWHJPIjtgNfA34CfAvYD1xyO9hcrfR9wCvIkn2A+SObi7dMed2m/PvcDuA4w8FA+Pr/kWjIQGZ1M7A7GAj3uBXoFpFoKLdpCogA/wD2AeuAX6O5jbRnOBINlQDPIu7lwYUg64Ae4EFTn2cRi+8IrT0ciYZ8wPOIq3giGAhPu1CsCGgAWpH9vhzxxX7zeRzxwxcR99MB9CE+2gnjwI+Bp4AXgUeAhN0LOlbaQJbMVeDnwUBY1wLXA/cihqZC8500JhC7cDgSDQ1o9DeAZ4BS4FEUy1vXLe1BlH84GAhf0xBeh7iQ9YBHo78dUsAZ4OVINDTo0LcYeAEYQCz4LOgQvhvYjezZcQeBJQjRnYDXoa9bzCAR18FINDRl068C+COyvI/lPjzbErM1WsuAnwKPa5CtQX7V+yk8Wcwx7wf2BwPhGpt+48DjiN7LrDrYEX4MeFXDGq9ByNY79CsE6oHfBAPhtTZ9eoA/IfrPgorwFmAFcNBBgbVAGKh06FdIVADPOJB+BdF/S+4DK8IGEhu/gL1rqAGeBHzaqhYOPuBJm+U9jej/CDlbzIrwNsQF2YWLJcheWciZzUUlYl9UAcdJIAa0ZTZaEf4e8JKDsF0szJ51Qj3wXZvnLwEPZTbkEv4icmhvtxmkDnE9Nwu+GQyEaxXP2oElCC9gdmh5L3AY+0B8F3NwPV5PkdHkb15a71t965LiQLXP8PlSqWQynownRqZHxgYSF670xLsvz6Sm3Z6lvaZOv7R4lgQOAd8A+mE24c1IXKpCPRJBuUJzacvSjeWbGsu8ZWVZDzyGUe6tKC/3VpTftmjl8g3lGyffmTjV2xXrvOxSxIZgIFyvCEP/DvwCMWJZS/oWZDn32gy8ExfhooHhaava0XhXZduGWWQtUOYtK9tW2bahrWpHo4HhJiz1oN5mfciyDohON7AeiVtVS6oYuNOFEny9antDo79ptZt3ABr9Tavvqtre4PK1O4OBcLFFexJJJK6HbMJrkChFhbWA4yyl0VL6pZqGOZBNo9HftHpdaatdGJmLMkRHK3RjGq5MwquQ3LAKrbqSvZ4iY2PFpmbd/ipsqvhqs9dT5CYNpdLxA+QsnkV4JfaE63SltpS21vgNf94RmM/w+1rczbJKxyHgNsgmXA18ZDPYcl2ptb66pbp9nVDnq3czlkrHEcwkRCbhciTToEKVrtTFRUu0+zqhumixm7FUfScw7U8m4WIkI6iC3+ZZFnyGb5Fu3wKPpdJxCkn/ZBG+hmbmzwnJVLKQNw+FQAlykMgiPIEsaxXiuqMnkomrc9Mr77FUOpYDk5BNeASJSFQY1ZU6OjPyiW5fJ4xMf6wtF7WO1Uj6J4vwvxFfrMJFXalDiUG3sbASg4kBN2OpdKxF+GURHsKesFOa9Do6Yx3D8WTcNiGug0QynuiKdQy7eEWl4yrMO+ZMwudRh2YgNwJamElNJ/85firvq5i3x091T7s7Lqp0bED4ZRE+DdyBOrF3DnPj66Az9t6lvnjvBd3+ueiL91zojL3nZnZjiI658AC3I2UUWeT+h2x61SxfQ27stHFi9Fjf+Xj/kJt3AN5P9A+dGD3e5/K1tyLRkNXNSAMwhlkzkjubJ5ESAxX+6kaDJMnU0dFDXe1jJ05Pzkw6ro7JmcnJ9rETp4+MHOpKknRbT3VI0X4PGQnJ3IzHYeSa4kXkeiMXF5Cz5R1uNOmKdQz3xnuutJS21tT56pdWFy2u9Bk+P0AimYiPTH88NpgYuNwZ6xieQ4oH4N1INPS+RbsXSVvtTjfkEu5HCki2IKkRKxxAjmGu8lozqenk2ckzF89OntF2b7pDo86ybkX49KcbrAzUAeCHNgIGkIutmwWv2dws/gB4NbPBinA7sAhJ6KlwECH+aWMQ9XXQZuTA8LfMRivCSaQ06FHUh4kppL5ibE5qFgZjwK8U16cliP7Pk2OLVD73DST7YZfVHwaexqHEYJ6QAJ6OREMqP/0Qov+sei67fNF+4IFINNRk0+ccsBczMF8gjAN7I9GQVZAB0AR8B0UVgB3hS8BzwL5INGR3bDyH3MUuxJ4eAPbYkC1HttpzKIrWnDKCx4A3gf2RaMgq55vGJaQW5C9Y++98MWOOvScSDancWjEyq2+SY6gyoVvF8zskQbBXo4qnDrmBdH0lo8BpnItaDMSeVAIPk08VTzAQzqzT+i/wVDAQ1pnFQpQtHYlEQ04HEC9yH/Z5HOq0tAnD9Uq8fZiX4cFA2C7DmYncwrQVSAYinbdOINmW/2BRmGZRepiJMlOnKeAJ7JOQ7gibwtO1lpsQ0v2WLxUQNoTXICWHbyN71zEGz6deejtStf5n4GXk6LhQKEZsxLcRwsd1X3Sq07LDcVNoM0LaLgwtJDab8pqR6nttsmkUsiL+KlIR/zqFr4jfihxoFpFnRfx8fPNwC+K/jyDGZ67fPDQgpQp3I9mYA9wk3zzkopYbX7Us4cZXLR8i8e1HwCeIFS4CPofcCa1AXNk64Mtmv4J+1TJfhDMRAL4CfAFJla5EfHIp4lImkeTbOPKDpL9beod5+m7J81n7FO//PWS9l1w3i+IAAAAASUVORK5CYII=';
let icon2 = 'image://data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADwAAAA8CAYAAAA6/NlyAAAABGdBTUEAALGPC/xhBQAACklpQ0NQc1JHQiBJRUM2MTk2Ni0yLjEAAEiJnVN3WJP3Fj7f92UPVkLY8LGXbIEAIiOsCMgQWaIQkgBhhBASQMWFiApWFBURnEhVxILVCkidiOKgKLhnQYqIWotVXDjuH9yntX167+3t+9f7vOec5/zOec8PgBESJpHmomoAOVKFPDrYH49PSMTJvYACFUjgBCAQ5svCZwXFAADwA3l4fnSwP/wBr28AAgBw1S4kEsfh/4O6UCZXACCRAOAiEucLAZBSAMguVMgUAMgYALBTs2QKAJQAAGx5fEIiAKoNAOz0ST4FANipk9wXANiiHKkIAI0BAJkoRyQCQLsAYFWBUiwCwMIAoKxAIi4EwK4BgFm2MkcCgL0FAHaOWJAPQGAAgJlCLMwAIDgCAEMeE80DIEwDoDDSv+CpX3CFuEgBAMDLlc2XS9IzFLiV0Bp38vDg4iHiwmyxQmEXKRBmCeQinJebIxNI5wNMzgwAABr50cH+OD+Q5+bk4eZm52zv9MWi/mvwbyI+IfHf/ryMAgQAEE7P79pf5eXWA3DHAbB1v2upWwDaVgBo3/ldM9sJoFoK0Hr5i3k4/EAenqFQyDwdHAoLC+0lYqG9MOOLPv8z4W/gi372/EAe/tt68ABxmkCZrcCjg/1xYW52rlKO58sEQjFu9+cj/seFf/2OKdHiNLFcLBWK8ViJuFAiTcd5uVKRRCHJleIS6X8y8R+W/QmTdw0ArIZPwE62B7XLbMB+7gECiw5Y0nYAQH7zLYwaC5EAEGc0Mnn3AACTv/mPQCsBAM2XpOMAALzoGFyolBdMxggAAESggSqwQQcMwRSswA6cwR28wBcCYQZEQAwkwDwQQgbkgBwKoRiWQRlUwDrYBLWwAxqgEZrhELTBMTgN5+ASXIHrcBcGYBiewhi8hgkEQcgIE2EhOogRYo7YIs4IF5mOBCJhSDSSgKQg6YgUUSLFyHKkAqlCapFdSCPyLXIUOY1cQPqQ28ggMor8irxHMZSBslED1AJ1QLmoHxqKxqBz0XQ0D12AlqJr0Rq0Hj2AtqKn0UvodXQAfYqOY4DRMQ5mjNlhXIyHRWCJWBomxxZj5Vg1Vo81Yx1YN3YVG8CeYe8IJAKLgBPsCF6EEMJsgpCQR1hMWEOoJewjtBK6CFcJg4Qxwicik6hPtCV6EvnEeGI6sZBYRqwm7iEeIZ4lXicOE1+TSCQOyZLkTgohJZAySQtJa0jbSC2kU6Q+0hBpnEwm65Btyd7kCLKArCCXkbeQD5BPkvvJw+S3FDrFiOJMCaIkUqSUEko1ZT/lBKWfMkKZoKpRzame1AiqiDqfWkltoHZQL1OHqRM0dZolzZsWQ8ukLaPV0JppZ2n3aC/pdLoJ3YMeRZfQl9Jr6Afp5+mD9HcMDYYNg8dIYigZaxl7GacYtxkvmUymBdOXmchUMNcyG5lnmA+Yb1VYKvYqfBWRyhKVOpVWlX6V56pUVXNVP9V5qgtUq1UPq15WfaZGVbNQ46kJ1Bar1akdVbupNq7OUndSj1DPUV+jvl/9gvpjDbKGhUaghkijVGO3xhmNIRbGMmXxWELWclYD6yxrmE1iW7L57Ex2Bfsbdi97TFNDc6pmrGaRZp3mcc0BDsax4PA52ZxKziHODc57LQMtPy2x1mqtZq1+rTfaetq+2mLtcu0W7eva73VwnUCdLJ31Om0693UJuja6UbqFutt1z+o+02PreekJ9cr1Dund0Uf1bfSj9Rfq79bv0R83MDQINpAZbDE4Y/DMkGPoa5hpuNHwhOGoEctoupHEaKPRSaMnuCbuh2fjNXgXPmasbxxirDTeZdxrPGFiaTLbpMSkxeS+Kc2Ua5pmutG003TMzMgs3KzYrMnsjjnVnGueYb7ZvNv8jYWlRZzFSos2i8eW2pZ8ywWWTZb3rJhWPlZ5VvVW16xJ1lzrLOtt1ldsUBtXmwybOpvLtqitm63Edptt3xTiFI8p0in1U27aMez87ArsmuwG7Tn2YfYl9m32zx3MHBId1jt0O3xydHXMdmxwvOuk4TTDqcSpw+lXZxtnoXOd8zUXpkuQyxKXdpcXU22niqdun3rLleUa7rrStdP1o5u7m9yt2W3U3cw9xX2r+00umxvJXcM970H08PdY4nHM452nm6fC85DnL152Xlle+70eT7OcJp7WMG3I28Rb4L3Le2A6Pj1l+s7pAz7GPgKfep+Hvqa+It89viN+1n6Zfgf8nvs7+sv9j/i/4XnyFvFOBWABwQHlAb2BGoGzA2sDHwSZBKUHNQWNBbsGLww+FUIMCQ1ZH3KTb8AX8hv5YzPcZyya0RXKCJ0VWhv6MMwmTB7WEY6GzwjfEH5vpvlM6cy2CIjgR2yIuB9pGZkX+X0UKSoyqi7qUbRTdHF09yzWrORZ+2e9jvGPqYy5O9tqtnJ2Z6xqbFJsY+ybuIC4qriBeIf4RfGXEnQTJAntieTE2MQ9ieNzAudsmjOc5JpUlnRjruXcorkX5unOy553PFk1WZB8OIWYEpeyP+WDIEJQLxhP5aduTR0T8oSbhU9FvqKNolGxt7hKPJLmnVaV9jjdO31D+miGT0Z1xjMJT1IreZEZkrkj801WRNberM/ZcdktOZSclJyjUg1plrQr1zC3KLdPZisrkw3keeZtyhuTh8r35CP5c/PbFWyFTNGjtFKuUA4WTC+oK3hbGFt4uEi9SFrUM99m/ur5IwuCFny9kLBQuLCz2Lh4WfHgIr9FuxYji1MXdy4xXVK6ZHhp8NJ9y2jLspb9UOJYUlXyannc8o5Sg9KlpUMrglc0lamUycturvRauWMVYZVkVe9ql9VbVn8qF5VfrHCsqK74sEa45uJXTl/VfPV5bdra3kq3yu3rSOuk626s91m/r0q9akHV0IbwDa0b8Y3lG19tSt50oXpq9Y7NtM3KzQM1YTXtW8y2rNvyoTaj9nqdf13LVv2tq7e+2Sba1r/dd3vzDoMdFTve75TsvLUreFdrvUV99W7S7oLdjxpiG7q/5n7duEd3T8Wej3ulewf2Re/ranRvbNyvv7+yCW1SNo0eSDpw5ZuAb9qb7Zp3tXBaKg7CQeXBJ9+mfHvjUOihzsPcw83fmX+39QjrSHkr0jq/dawto22gPaG97+iMo50dXh1Hvrf/fu8x42N1xzWPV56gnSg98fnkgpPjp2Snnp1OPz3Umdx590z8mWtdUV29Z0PPnj8XdO5Mt1/3yfPe549d8Lxw9CL3Ytslt0utPa49R35w/eFIr1tv62X3y+1XPK509E3rO9Hv03/6asDVc9f41y5dn3m978bsG7duJt0cuCW69fh29u0XdwruTNxdeo94r/y+2v3qB/oP6n+0/rFlwG3g+GDAYM/DWQ/vDgmHnv6U/9OH4dJHzEfVI0YjjY+dHx8bDRq98mTOk+GnsqcTz8p+Vv9563Or59/94vtLz1j82PAL+YvPv655qfNy76uprzrHI8cfvM55PfGm/K3O233vuO+638e9H5ko/ED+UPPR+mPHp9BP9z7nfP78L/eE8/stRzjPAAAAIGNIUk0AAHomAACAhAAA+gAAAIDoAAB1MAAA6mAAADqYAAAXcJy6UTwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAiMSURBVGiB5ZtrbBxXFcd/Ozu7jR07wamN7do4iZ3UDqmatjYfWowTiUfT1hTxCQQlQL8AEiWlTUMRBBqKeDQUtbT9gFTR0AoQH0BChLTQAnaagiLFpY3iPNzacdPED5wHqR3bWY9n+XDuprPruTN31hMnUv/SSquZe885/72Pc+65ZxPZbJb3EqzLbcBCw859mfz3w5dCfiXQBqwGGoDlQAVQrnQ7wDhwFngLOA68AewHTsVtTOnN294lHCNWAJ3AeoTwf4Be4K8IoVPABJAB0kAZsAyoA1YCnwC+pdp1A7uAwbiMi4uwBWwAvgRUI+QeAg4DbkC/DHBGfd5ECObkrQFuBX4JjAI7ga4QeaGIg3AH8HXE+F8Rg1Gqf6/6PKZ0bAK+CjwJ7ClW8HwIXwNsQabwz4G985AVBBf5EbuADwP3A58GdgBDUYUVu0vfDjyHTNnPcunIFuIVpa9X6b89qoCoI2who9oO3AMciqowBmSAp4F/AT8BrgN+huEyijLCaeCniHv5PJeHrBeHlB0NiF1pk06mI7wIeBxxFd9G/KcpbKAFuB5Z73WILy5R76cQP3wScT8HgCOGOsaBexGP8ASwGZgO6pDIhZYBgYeFTJkLwHcw34EbgduQjabcsE8OE8i+8DwwYNDeAn4IlAL36WwsvXmb0ZS+HxmN7+kEFWAl8H3EnWwkOlmQYGSjkvGQkhkEV+m8StmrRdiU/jjwEWStzIS0TSO+shNIhrQ1RQJoBW5AIq5nkU3LDzPAVuA3wGvAi36Ngkb4GiXgQWStBKEW8YufIj6yXiSV7B1Klw7jiL1bEfvnIIjwFuB3hO/Gq5UhjSHt4kAj8CjQHNDmEPBbxP450BHuAOqRKRSEZuBHwNKQdnGiHNmggkg/h9jfUfjCj7CFxMa/INg11ALbEJe10FikdOumt4PYv5mCJeZHeAPigoLCxTSyVhZyZAuxVNmgCzj2ApPAR70P/Qh/EXgmRNkmFmbNhqER+ELA+2eAu7wPCglfixzauwKErERcz5WCTyIRnB+6gKsRXsBcP3wbEt0EBRibKMb1WLZlv/+GmuSy5mqrtLoiYZcsIuu6WWdy2p06dW72zNFR57+vjeA6Uc/SSWXTD3zeucBuJIjpg7mE25HIRodGJBCIBLv6pppUfceaRLp8cd6LhGUl0kvKkuklZcmljXWpuvbzMyf2HHZGXx2JqKJN2eYXhv4T2I5sYnlTugqZzocDBHci0Y8ZElYiverONenGO9rmkPVrni5fnG68oy296s41JCxzPWKTbpkdQaZ1JeQTbgVeRT+dU8AtEYwg3dTZYleta4rSB8CuWteUbupsidjtFsTGQrhIIrEV8gmvJjiqagZCRykHu6atthiyF/tXrWuyq1uDwshCLEYfjPSiNi4v4eVIbliH641VW7aVql+/1ri9BqmGDWux7ChJCp2Nb6F2cq+wBoIJhx3RLsKubq1NpErnHYEl7NJFdnVblFHW2TgIfADyCVcApwOE1ZlqTVZcW2PaNlTWskiydDaeRZ3LvYTLkEyDDu8z1WqVVhm3DZVVUhlFlq7tBGr/8RJOoT9cw7s5qFAk7JKrTNvGLEtnYwZJ/+QRnsEw8xeKrDvfm4e4kUYOEnmEJ5BprcOUqfSsM3mhOLv8ZE1FkaWzsQw4D/mEzyIRiQ7/M9XqTp15x7RtuKxTxnrR21iBSlN5Cb+N+GIdTppqnT3bFzUW1ss6E0mWzsYVCL88woMEEz5mqtUZ7RnOzkwGJsRNkHUmp53RnuEIXXQ2LkfdMXsJv0FwnuiAsVrXcWdOdM/7Kmbm7e5e3JkoG6DOxhaEXx7hHuBG9Im9o6iFbwJnZP+QM3ag37T9nP5jr/c7I/ujjO4kYmMhEkheez/kkxtDFr1ulGeQGztjZPr/fGT2dO9glD4As6cPDWb6dx2J2O0V/C8LWoBzqJqRwtHci5QZ6PCXSCZk3eyFvj8ezAzs7slmxkNnRzYzfj4zsLvnQt8fDpJ1o9ZT7dY8vxVPQrIw4/E8cgv3BDDr07kfOVveGMUSZ7Rn2Bl7fdSubq1NLmuusUoqlybskhKArDM1pVI8I85oz3ARKR6UTW/6PE8iaat7cg8KCfchBSQdSGrEDzuRY1i0vJbruM7wvpPO8D5j92aIWfRZ1vUIn77cA78Naidwd4CCAeRi60rBLvTu6MvIddFF+BHuQq4d2wOUPIvZve2lxjH010HtyIHhb96HfoRdpDToPvSHiQxSX3GuKDPjwTngx/if8NKI/Y9TsBfpfO4eJPsRlNUfBh4mpMTgEmFa6db56bsQ++fUcwXli3YgJUIfDGhzFPgu4ffHcWJc6fQLMkDs/Rxi/xwEER4CHkGmbtCx8ShyF7sQa3oAeAA92TLE3kfQFK2FZQRfBF5Gfi2/nG8OQ8qQP+Hvv+eLWSX7AfQnohRi58sUbFRemKRAH0VCtu0h7XMFY99E4vK40KNkPo0+BWUhV0SziL1amBB2kZqJqxHSYQHHMaV8M/ACxa3vCdX3XiUr6GiaVHZVIksrMFIzqdPKIY2sj9xleFCG04vCwrR6JAORy1tPI9mWE0QvTFusbMogBXNBScjIBeIZ5Bfcgjj7B/GEbAFwgIPqEydWIyWH+5C1axSDRy0udZEd8GPAU8DvgV8TXsMVJ1JIlcJnEMIvRelcbPnwS0rpWoR0UBgaJ9qVvrVI9X0ksjC/AvEhZPfsAL4BfAWpiO9m/hXxXljIqeduJMZ/jMtUEZ/DHuSAvQE5nWxF/PcLyOZTDHkL2eg2IuWPY8gRsKtIeRcR1588XOAf6rMCuY3fjriy3L9ajiPx7WngHWQzs4ElyJ1QPVK2cB1wk2rXDXyNK/BfLV4MIqetJxHf+CFgFTJaDcgtXiniUs4jybdx5Ac5DvwdcTWx/28JPH74vYL/A+K/O8PQf/1+AAAAAElFTkSuQmCCtH2K93/H70tXUY8yQwAAAABJRU5ErkJggg==';
let color1 = new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 0,color: '#0A3869'},{offset: 1,color: '#93E68F'}
]);
let color2 = new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 0,color: '#0A3869'},{offset: 1,color: '#F5C682'}
]);
let dataArr = [{value: 100,name: '10-30',itemStyle: {color: color1}
},
{value: 90,name: '10-31',itemStyle: {color: color2}
},
{value: 80,name: '11-01',itemStyle: {color: color1}
},
{value: 60,name: '11-02',itemStyle: {color: color2}
}
];
let dataArr1 = [{value: 100,name: '10-30',symbol: icon1
},
{value: 90,name: '10-31',symbol: icon2
},
{value: 80,name: '11-01',symbol: icon1
},
{value: 60,name: '11-02',symbol: icon2
}
];
let dataArr2 = [{value: 100,itemStyle: {color: new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 1,color: '#00000000'},{offset: 1,color: '#0A3869'},{offset: 1,color: '#0A3869'}])}
},
{value: 100,itemStyle: {color: new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 0.9,color: '#00000000'},{offset: 0.9,color: '#0A3869'},{offset: 1,color: '#0A3869'}])}
},
{value: 100,itemStyle: {color: new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 0.8,color: '#00000000'},{offset: 0.8,color: '#0A3869'},{offset: 1,color: '#0A3869'}])}
},
{value: 100,itemStyle: {color: new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 0.6,color: '#00000000'},{offset: 0.6,color: '#0A3869'},{offset: 1,color: '#0A3869'}])}
}
];option = {backgroundColor: '#021334',xAxis: {show: false},tooltip: {show: true},yAxis: [{triggerEvent: true,show: true,data: ['10-30', '10-31', '11-01', '11-02'],axisLine: {show: false},splitLine: {show: false},axisTick: {show: false},axisLabel: {show: true,margin: -40,interval: 0,inside: true,padding: [0, 0, -5, 0],color: '#ffffff',fontSize: 14,align: 'left'}},{show: true,offset: 0,data: ['100', '90', '80', '60'],axisLine: {show: false},splitLine: {show: false},axisTick: {show: false},axisLabel: {show: true,margin: -40,interval: 0,inside: true,padding: [0, 0, -5, 0],color: '#ffffff',fontSize: 14,align: 'right'}}],series: [{type: 'pictorialBar',barMinWidth: '10',symbol: 'path://M 0 5 L 17 0 L 17 10 z',symbolOffset: [0, 5],yAxisIndex: 0,data: dataArr,barWidth: 2,z: 1,itemStyle: {normal: {barBorderRadius: 20}}},{data: dataArr1,type: 'pictorialBar',barMaxWidth: 20,symbolPosition: 'end',symbolOffset: [15, 0],symbolSize: [30, 30],zlevel: 2,silent: true},{type: 'bar',barGap: '-100%',yAxisIndex: 0,data: dataArr2,barWidth: 10,itemStyle: {barBorderRadius: 0},z: 0,silent: true}]
};

改造一下就可以用了


let icon1 = 'image://data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADwAAAA8CAYAAAA6/NlyAAAABGdBTUEAALGPC/xhBQAACklpQ0NQc1JHQiBJRUM2MTk2Ni0yLjEAAEiJnVN3WJP3Fj7f92UPVkLY8LGXbIEAIiOsCMgQWaIQkgBhhBASQMWFiApWFBURnEhVxILVCkidiOKgKLhnQYqIWotVXDjuH9yntX167+3t+9f7vOec5/zOec8PgBESJpHmomoAOVKFPDrYH49PSMTJvYACFUjgBCAQ5svCZwXFAADwA3l4fnSwP/wBr28AAgBw1S4kEsfh/4O6UCZXACCRAOAiEucLAZBSAMguVMgUAMgYALBTs2QKAJQAAGx5fEIiAKoNAOz0ST4FANipk9wXANiiHKkIAI0BAJkoRyQCQLsAYFWBUiwCwMIAoKxAIi4EwK4BgFm2MkcCgL0FAHaOWJAPQGAAgJlCLMwAIDgCAEMeE80DIEwDoDDSv+CpX3CFuEgBAMDLlc2XS9IzFLiV0Bp38vDg4iHiwmyxQmEXKRBmCeQinJebIxNI5wNMzgwAABr50cH+OD+Q5+bk4eZm52zv9MWi/mvwbyI+IfHf/ryMAgQAEE7P79pf5eXWA3DHAbB1v2upWwDaVgBo3/ldM9sJoFoK0Hr5i3k4/EAenqFQyDwdHAoLC+0lYqG9MOOLPv8z4W/gi372/EAe/tt68ABxmkCZrcCjg/1xYW52rlKO58sEQjFu9+cj/seFf/2OKdHiNLFcLBWK8ViJuFAiTcd5uVKRRCHJleIS6X8y8R+W/QmTdw0ArIZPwE62B7XLbMB+7gECiw5Y0nYAQH7zLYwaC5EAEGc0Mnn3AACTv/mPQCsBAM2XpOMAALzoGFyolBdMxggAAESggSqwQQcMwRSswA6cwR28wBcCYQZEQAwkwDwQQgbkgBwKoRiWQRlUwDrYBLWwAxqgEZrhELTBMTgN5+ASXIHrcBcGYBiewhi8hgkEQcgIE2EhOogRYo7YIs4IF5mOBCJhSDSSgKQg6YgUUSLFyHKkAqlCapFdSCPyLXIUOY1cQPqQ28ggMor8irxHMZSBslED1AJ1QLmoHxqKxqBz0XQ0D12AlqJr0Rq0Hj2AtqKn0UvodXQAfYqOY4DRMQ5mjNlhXIyHRWCJWBomxxZj5Vg1Vo81Yx1YN3YVG8CeYe8IJAKLgBPsCF6EEMJsgpCQR1hMWEOoJewjtBK6CFcJg4Qxwicik6hPtCV6EvnEeGI6sZBYRqwm7iEeIZ4lXicOE1+TSCQOyZLkTgohJZAySQtJa0jbSC2kU6Q+0hBpnEwm65Btyd7kCLKArCCXkbeQD5BPkvvJw+S3FDrFiOJMCaIkUqSUEko1ZT/lBKWfMkKZoKpRzame1AiqiDqfWkltoHZQL1OHqRM0dZolzZsWQ8ukLaPV0JppZ2n3aC/pdLoJ3YMeRZfQl9Jr6Afp5+mD9HcMDYYNg8dIYigZaxl7GacYtxkvmUymBdOXmchUMNcyG5lnmA+Yb1VYKvYqfBWRyhKVOpVWlX6V56pUVXNVP9V5qgtUq1UPq15WfaZGVbNQ46kJ1Bar1akdVbupNq7OUndSj1DPUV+jvl/9gvpjDbKGhUaghkijVGO3xhmNIRbGMmXxWELWclYD6yxrmE1iW7L57Ex2Bfsbdi97TFNDc6pmrGaRZp3mcc0BDsax4PA52ZxKziHODc57LQMtPy2x1mqtZq1+rTfaetq+2mLtcu0W7eva73VwnUCdLJ31Om0693UJuja6UbqFutt1z+o+02PreekJ9cr1Dund0Uf1bfSj9Rfq79bv0R83MDQINpAZbDE4Y/DMkGPoa5hpuNHwhOGoEctoupHEaKPRSaMnuCbuh2fjNXgXPmasbxxirDTeZdxrPGFiaTLbpMSkxeS+Kc2Ua5pmutG003TMzMgs3KzYrMnsjjnVnGueYb7ZvNv8jYWlRZzFSos2i8eW2pZ8ywWWTZb3rJhWPlZ5VvVW16xJ1lzrLOtt1ldsUBtXmwybOpvLtqitm63Edptt3xTiFI8p0in1U27aMez87ArsmuwG7Tn2YfYl9m32zx3MHBId1jt0O3xydHXMdmxwvOuk4TTDqcSpw+lXZxtnoXOd8zUXpkuQyxKXdpcXU22niqdun3rLleUa7rrStdP1o5u7m9yt2W3U3cw9xX2r+00umxvJXcM970H08PdY4nHM452nm6fC85DnL152Xlle+70eT7OcJp7WMG3I28Rb4L3Le2A6Pj1l+s7pAz7GPgKfep+Hvqa+It89viN+1n6Zfgf8nvs7+sv9j/i/4XnyFvFOBWABwQHlAb2BGoGzA2sDHwSZBKUHNQWNBbsGLww+FUIMCQ1ZH3KTb8AX8hv5YzPcZyya0RXKCJ0VWhv6MMwmTB7WEY6GzwjfEH5vpvlM6cy2CIjgR2yIuB9pGZkX+X0UKSoyqi7qUbRTdHF09yzWrORZ+2e9jvGPqYy5O9tqtnJ2Z6xqbFJsY+ybuIC4qriBeIf4RfGXEnQTJAntieTE2MQ9ieNzAudsmjOc5JpUlnRjruXcorkX5unOy553PFk1WZB8OIWYEpeyP+WDIEJQLxhP5aduTR0T8oSbhU9FvqKNolGxt7hKPJLmnVaV9jjdO31D+miGT0Z1xjMJT1IreZEZkrkj801WRNberM/ZcdktOZSclJyjUg1plrQr1zC3KLdPZisrkw3keeZtyhuTh8r35CP5c/PbFWyFTNGjtFKuUA4WTC+oK3hbGFt4uEi9SFrUM99m/ur5IwuCFny9kLBQuLCz2Lh4WfHgIr9FuxYji1MXdy4xXVK6ZHhp8NJ9y2jLspb9UOJYUlXyannc8o5Sg9KlpUMrglc0lamUycturvRauWMVYZVkVe9ql9VbVn8qF5VfrHCsqK74sEa45uJXTl/VfPV5bdra3kq3yu3rSOuk626s91m/r0q9akHV0IbwDa0b8Y3lG19tSt50oXpq9Y7NtM3KzQM1YTXtW8y2rNvyoTaj9nqdf13LVv2tq7e+2Sba1r/dd3vzDoMdFTve75TsvLUreFdrvUV99W7S7oLdjxpiG7q/5n7duEd3T8Wej3ulewf2Re/ranRvbNyvv7+yCW1SNo0eSDpw5ZuAb9qb7Zp3tXBaKg7CQeXBJ9+mfHvjUOihzsPcw83fmX+39QjrSHkr0jq/dawto22gPaG97+iMo50dXh1Hvrf/fu8x42N1xzWPV56gnSg98fnkgpPjp2Snnp1OPz3Umdx590z8mWtdUV29Z0PPnj8XdO5Mt1/3yfPe549d8Lxw9CL3Ytslt0utPa49R35w/eFIr1tv62X3y+1XPK509E3rO9Hv03/6asDVc9f41y5dn3m978bsG7duJt0cuCW69fh29u0XdwruTNxdeo94r/y+2v3qB/oP6n+0/rFlwG3g+GDAYM/DWQ/vDgmHnv6U/9OH4dJHzEfVI0YjjY+dHx8bDRq98mTOk+GnsqcTz8p+Vv9563Or59/94vtLz1j82PAL+YvPv655qfNy76uprzrHI8cfvM55PfGm/K3O233vuO+638e9H5ko/ED+UPPR+mPHp9BP9z7nfP78L/eE8/stRzjPAAAAIGNIUk0AAHomAACAhAAA+gAAAIDoAAB1MAAA6mAAADqYAAAXcJy6UTwAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAipSURBVGiB5ZttcFTVGcd/ezcJu3lpElgrAYQklJIXkmqhDLUMYINYHTpOP9Wplr7MfizasdLqFmdsdbYobadqP+5UxGmdfuyM5aUwNCp2sBbEvBMkibYQaFeTmGR3CcluPzx3YXdzz73nZjeRGf8zmcmce+55nv+ec57nOc95rieVSvFZgvFpK7DQKEr/c3tn6XyMHwA2AGuAlcAqoBqoMGVPA+PACPAB8CFwHvgXEC20MmdbYjcIFxC1wE5gK0L4XaAbOIoQigITwBRQApQDi4HlQB2wA/iZ2e914DVgqFDKedJ7OM8ZNoBtwPeBWxFyR4FeIDnH8RqBe8y/K8ABoH2O4wEyw4UgvAX4ETJjf8hXKQsYpoxdyGr4PfDGXAbKd0kvAx5DlvBvgZN5jGWHJPIjtgNfA34CfAvYD1xyO9hcrfR9wCvIkn2A+SObi7dMed2m/PvcDuA4w8FA+Pr/kWjIQGZ1M7A7GAj3uBXoFpFoKLdpCogA/wD2AeuAX6O5jbRnOBINlQDPIu7lwYUg64Ae4EFTn2cRi+8IrT0ciYZ8wPOIq3giGAhPu1CsCGgAWpH9vhzxxX7zeRzxwxcR99MB9CE+2gnjwI+Bp4AXgUeAhN0LOlbaQJbMVeDnwUBY1wLXA/cihqZC8500JhC7cDgSDQ1o9DeAZ4BS4FEUy1vXLe1BlH84GAhf0xBeh7iQ9YBHo78dUsAZ4OVINDTo0LcYeAEYQCz4LOgQvhvYjezZcQeBJQjRnYDXoa9bzCAR18FINDRl068C+COyvI/lPjzbErM1WsuAnwKPa5CtQX7V+yk8Wcwx7wf2BwPhGpt+48DjiN7LrDrYEX4MeFXDGq9ByNY79CsE6oHfBAPhtTZ9eoA/IfrPgorwFmAFcNBBgbVAGKh06FdIVADPOJB+BdF/S+4DK8IGEhu/gL1rqAGeBHzaqhYOPuBJm+U9jej/CDlbzIrwNsQF2YWLJcheWciZzUUlYl9UAcdJIAa0ZTZaEf4e8JKDsF0szJ51Qj3wXZvnLwEPZTbkEv4icmhvtxmkDnE9Nwu+GQyEaxXP2oElCC9gdmh5L3AY+0B8F3NwPV5PkdHkb15a71t965LiQLXP8PlSqWQynownRqZHxgYSF670xLsvz6Sm3Z6lvaZOv7R4lgQOAd8A+mE24c1IXKpCPRJBuUJzacvSjeWbGsu8ZWVZDzyGUe6tKC/3VpTftmjl8g3lGyffmTjV2xXrvOxSxIZgIFyvCEP/DvwCMWJZS/oWZDn32gy8ExfhooHhaava0XhXZduGWWQtUOYtK9tW2bahrWpHo4HhJiz1oN5mfciyDohON7AeiVtVS6oYuNOFEny9antDo79ptZt3ABr9Tavvqtre4PK1O4OBcLFFexJJJK6HbMJrkChFhbWA4yyl0VL6pZqGOZBNo9HftHpdaatdGJmLMkRHK3RjGq5MwquQ3LAKrbqSvZ4iY2PFpmbd/ipsqvhqs9dT5CYNpdLxA+QsnkV4JfaE63SltpS21vgNf94RmM/w+1rczbJKxyHgNsgmXA18ZDPYcl2ptb66pbp9nVDnq3czlkrHEcwkRCbhciTToEKVrtTFRUu0+zqhumixm7FUfScw7U8m4WIkI6iC3+ZZFnyGb5Fu3wKPpdJxCkn/ZBG+hmbmzwnJVLKQNw+FQAlykMgiPIEsaxXiuqMnkomrc9Mr77FUOpYDk5BNeASJSFQY1ZU6OjPyiW5fJ4xMf6wtF7WO1Uj6J4vwvxFfrMJFXalDiUG3sbASg4kBN2OpdKxF+GURHsKesFOa9Do6Yx3D8WTcNiGug0QynuiKdQy7eEWl4yrMO+ZMwudRh2YgNwJamElNJ/85firvq5i3x091T7s7Lqp0bED4ZRE+DdyBOrF3DnPj66Az9t6lvnjvBd3+ueiL91zojL3nZnZjiI658AC3I2UUWeT+h2x61SxfQ27stHFi9Fjf+Xj/kJt3AN5P9A+dGD3e5/K1tyLRkNXNSAMwhlkzkjubJ5ESAxX+6kaDJMnU0dFDXe1jJ05Pzkw6ro7JmcnJ9rETp4+MHOpKknRbT3VI0X4PGQnJ3IzHYeSa4kXkeiMXF5Cz5R1uNOmKdQz3xnuutJS21tT56pdWFy2u9Bk+P0AimYiPTH88NpgYuNwZ6xieQ4oH4N1INPS+RbsXSVvtTjfkEu5HCki2IKkRKxxAjmGu8lozqenk2ckzF89OntF2b7pDo86ybkX49KcbrAzUAeCHNgIGkIutmwWv2dws/gB4NbPBinA7sAhJ6KlwECH+aWMQ9XXQZuTA8LfMRivCSaQ06FHUh4kppL5ibE5qFgZjwK8U16cliP7Pk2OLVD73DST7YZfVHwaexqHEYJ6QAJ6OREMqP/0Qov+sei67fNF+4IFINNRk0+ccsBczMF8gjAN7I9GQVZAB0AR8B0UVgB3hS8BzwL5INGR3bDyH3MUuxJ4eAPbYkC1HttpzKIrWnDKCx4A3gf2RaMgq55vGJaQW5C9Y++98MWOOvScSDancWjEyq2+SY6gyoVvF8zskQbBXo4qnDrmBdH0lo8BpnItaDMSeVAIPk08VTzAQzqzT+i/wVDAQ1pnFQpQtHYlEQ04HEC9yH/Z5HOq0tAnD9Uq8fZiX4cFA2C7DmYncwrQVSAYinbdOINmW/2BRmGZRepiJMlOnKeAJ7JOQ7gibwtO1lpsQ0v2WLxUQNoTXICWHbyN71zEGz6deejtStf5n4GXk6LhQKEZsxLcRwsd1X3Sq07LDcVNoM0LaLgwtJDab8pqR6nttsmkUsiL+KlIR/zqFr4jfihxoFpFnRfx8fPNwC+K/jyDGZ67fPDQgpQp3I9mYA9wk3zzkopYbX7Us4cZXLR8i8e1HwCeIFS4CPofcCa1AXNk64Mtmv4J+1TJfhDMRAL4CfAFJla5EfHIp4lImkeTbOPKDpL9beod5+m7J81n7FO//PWS9l1w3i+IAAAAASUVORK5CYII=';
let color1 = new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: 0,color: '#0A3869'},{offset: 1,color: '#93E68F'}
]);let process = 10
let dataArr = [{value: process,name: '10-30',itemStyle: {color: color1}
},];
let dataArr1 = [{value: process,name: '10-30',symbol: icon1
},];
let dataArr2 = [{value: 100,itemStyle: {color: new echarts.graphic.LinearGradient(0, 0, 1, 0, [{offset: process/100,color: '#00000000'},{offset: process/100,color: '#0A3869'},{offset: 1,color: '#0A3869'}])}
},];option = {backgroundColor: '#021334',xAxis: {show: false},tooltip: {show: true},yAxis: [{triggerEvent: true,show: false,data: ['10-30'],},{show: false,offset: 0,data: ['100',],}],series: [{type: 'pictorialBar',barMinWidth: '10',symbol: 'path://M 0 5 L 17 0 L 17 10 z',symbolOffset: [0, 5],yAxisIndex: 0,data: dataArr,barWidth: 2,z: 1,itemStyle: {normal: {barBorderRadius: 20}}},{data: dataArr1,type: 'pictorialBar',barMaxWidth: 20,symbolPosition: 'end',symbolOffset: [15, 0],symbolSize: [30, 30],zlevel: 2,silent: true},{type: 'bar',barGap: '-100%',yAxisIndex: 0,data: dataArr2,barWidth: 10,itemStyle: {barBorderRadius: 0},z: 0,silent: true}]
};