. - 力扣(LeetCode)
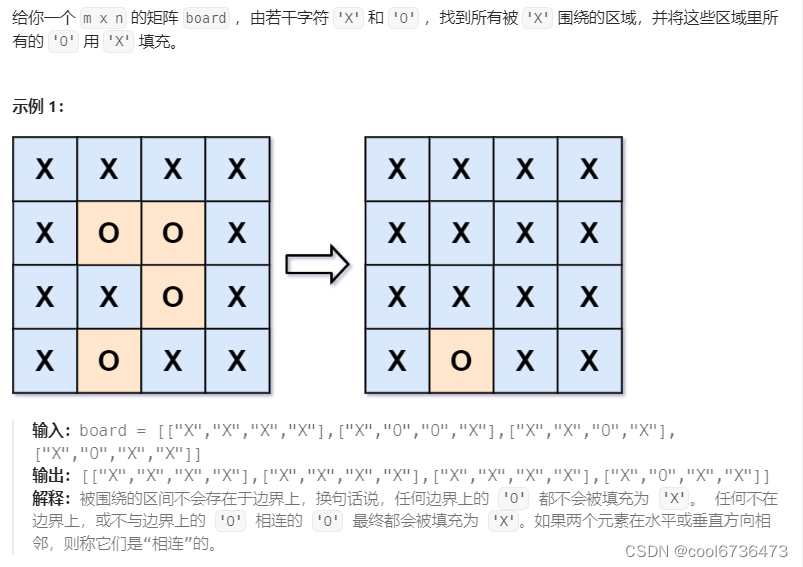
最开始也是考虑使用dfs,对于矩阵中的每个点,如果能到达边界的O,则跳过继续dfs。否则如果上下左右四个方向都无法到达边界的O,则说明当前的无法到达,在一个set中记录他的行数列数。
最后对每个记录的点标记为X即可。
但是有问题,首先可能会出现永久递归无法跳出来。如果使用父节点记录当前节点的前一个节点,则如果父节点恰好通往边界O,会导致错误。使用visited来记录状态也不行。
应该反向思维,从每个边界O出发dfs。
思路:对于边界上的每一个点进行dfs。如果当前点为X则直接跳过。如果当前点为O,则把O该为A,继续dfs。
使用A来记录从边界上的O所能够到达的点。
遍历完之后,再把矩阵中的O改为X,表示未与边界O相连。把矩阵中的A该为O,表示与边界相连的O,不变。
注意dfs函数中,如果发现不是X不能直接else,而要判断是不是为O,为O才继续dfs。
如果不这样的话当前为A也会继续dfs,导致永远无法停止的递归。
class Solution {
public:void dfs(vector<vector<char>>& board,int row,int col){if(board[row][col]=='X')return;else if(board[row][col]=='O'){board[row][col]='A';if(row>0)dfs(board,row-1,col);if(row<board.size()-1)dfs(board,row+1,col);if(col>0)dfs(board,row,col-1);if(col<board[0].size()-1)dfs(board,row,col+1);}}void solve(vector<vector<char>>& board) {for(int i=0;i<board.size();i++){dfs(board,i,0);dfs(board,i,board[0].size()-1);}for(int i=1;i<board[0].size()-1;i++){dfs(board,0,i);dfs(board,board.size()-1,i);}for(int i=0;i<board.size();i++){for(int j=0;j<board[0].size();j++){if(board[i][j]=='O')board[i][j]='X';else if(board[i][j]=='A')board[i][j]='O';}}}
};