1.二叉搜索树（BST Binary Search Tree）

1.1二叉搜索树的概念

二叉搜索树又称二叉排序树，它具有以下特点：

如果它的左子树不为空，则左子树所有节点的值都小于根节点的值。
如果它的右子树不为空，则右子树所有节点的值都大于根节点的值。
它的左右子树也分别为二叉搜索树。

2.2二叉搜索树的操作

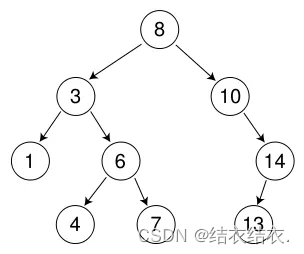
int a[] = {8,3,1,10,6,4,7,14,13};

2.2.1二叉搜索树的查找

a.从根节点出发，如果要找的值大于当前的节点值，去右边找，
如果要找的值小于当前的节点值，则去左边找，
如果相等则表示找到了。
b.如果值存在的话，最多查找高度次

2.2.2二叉搜索树的插入

a.如果树为空，则直接新增节点，赋值root指针
b.树不为空，按二叉搜索树性质查找插入位置，插入新节点

2.2.3二叉搜索树的删除

首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情况：
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况，实际情况a可以与情况b或者c合并起来，因此真正的删除过程如下：
情况b：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
情况c：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
情况d：在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题–替换法删除

2.3二叉搜索树的实现

2.3.1二叉搜索的基本结构

利用C++的模板实现泛型编程。

template <class K>
struct BSTNode
{BSTNode(const K& key = K()):_left(nullptr),_right(nullptr),_key(key){}BSTNode<K>* _left;BSTNode<K>* _right;K _key;
};
template <class K>
class BSTree
{typedef BSTNode<K> Node;typedef Node* pNode;
public:BSTree()//构造:_root(nullptr){}~BSTree()//销毁{}
private:pNode _root;
};

2.3.2查找节点

a.从根节点出发，如果要找的值大于当前的节点值，去右边找，
如果要找的值小于当前的节点值，则去左边找，
如果相等则表示找到了。
b.如果值存在的话，最多查找高度次

bool Find(const K& key){if (!_root) return nullptr;pNode cur = _root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return true;}}return false;}

2.3.3插入节点

a.如果树为空，则直接新增节点，赋值root指针
b.树不为空，按二叉搜索树性质查找插入位置，插入新节点

//插入bool Insert(const K& key = K()){if (!_root){_root = new Node(key);return true;}pNode cur = _root;pNode parent = nullptr;//引入父节点的目的是为了方便在后续，找到插入位置的父节点。如果没有父节点我们将无法插入while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (key > parent->_key){parent->_right = cur;}else if (key < parent->_key){parent->_left = cur;}return true;}

父节点的引入，方便找到插入位置的父节点。最后的if判断是为了确定插入的位置。

2.3.4删除节点

要删除节点我们首先要查找节点的位置。但我们查找成功时，此节点可能存在3种状态：
1.度为0的节点
2.度为1的节点
3.度为2的节点
那么这三种情况我们要如何删除呢？度为0我们可以直接删除，如果直接删除度为1的节点，那么就会造成节点丢失了。

删除度为1的节点

当我们要删除14时，我们可以先把14的父节点10的右指针指向13，然后再把14删除。

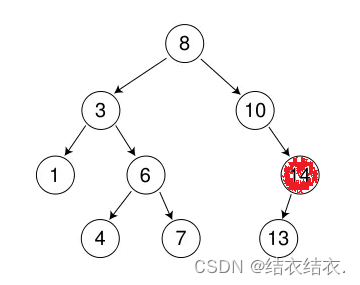
删除度为2的节点

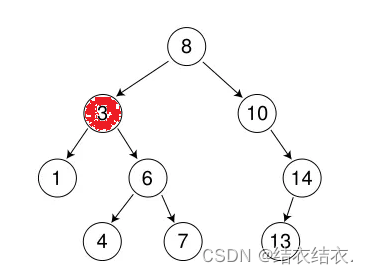
当我们删除3的时候，要怎么办呢？直接删除显然不行，如果让父节点来指向它的左右节点也不现实，毕竟有两个孩子嘛。
还记得堆的删除吗？当我们要删除堆顶元素时，我们会把堆顶元素和堆底元素的值调换再删除堆底元素，最后在进行向下调整。
我们也可以利用这个思想，我把3和4交换。为什么一定要和4交换呢？首先4在3的右边便确定了它一定会大于3。大于3的话肯定会大于3的左子树。然后又因为它在3右子树的左边，便又确定了它一定会小于3的右子树。最后我们在删除交换后的3节点就可以了。这种做法既可以删除3节点又不会影响二叉搜索树的规则。
，

实现

初版

//删除bool erase(const K& key = K()){pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{//找到了if (cur->_left == nullptr)//度为0或者度为1，因为两种删除方法可以重和。所以写在一起{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_right;}delete cur;return true;}else//度为2的节点{pNode leftnode = cur->_right;while (leftnode->_left)//找到最左边的节点{leftnode = leftnode->_left;}cur->_key = leftnode->_key;//因为leftnode为要删除的位置，所以可以直接给cur赋值delete leftnode;return true;}}}return false;}

下面来看看效果，那么我们要实现一下中序遍历

中序遍历

void Print(){_Print(_root);cout << endl;}
private:void _Print(pNode root){if (root == nullptr){return;}_Print(root->_left);cout << root->_key << " ";_Print(root->_right);}

因为打印不需要传参数，但是递归需要传参数。那么我们就可以在类里面在建立一个新的子函数，将子函数放在private里面避免在外被访问。
下面我们来看看插入效果

然后我们再看看删除效果

出错了！可以看出是删除度为2时出的问题。
为什么会这样呢？原因就是我们指向了野指针，直接删除leftnode时，其父节点的指针会指向野指针。除此之外还有一个问题，如果我们删除的是根节点，此时我们的parent节点指向空，在后序便会出问题。为了处理这个问题我们要在度为1和2都加上一个判断

删除节点的最终版本

//删除bool erase(const K& key = K()){pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{//找到了if (cur->_left == nullptr)//度为0或者度为1，因为两种删除方法可以重和。所以写在一起{if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;return true;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else {if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_right;}}delete cur;return true;}else//度为2的节点{pNode NodeParent = cur;pNode leftnode = cur->_right;while (leftnode->_left)//找到最左边的节点{NodeParent = leftnode;leftnode = leftnode->_left;}cur->_key = leftnode->_key;//因为leftnode为要删除的位置，所以可以直接给cur赋值if (leftnode == NodeParent->_left)NodeParent->_left = leftnode->_right;elseNodeParent->_right = leftnode->_right;delete leftnode;return true;}}}return false;}

二叉搜索树（递归实现）

写完迭代的代码，下面我们来看看，如何利用递归实现二叉搜索树

递归查找节点

bool FindR(const K&key){return _FindR(_root, key);}private:bool _FindR(pNode root, const K& key){if (!root) return false;if (key > root->_key){return _FindR(root->_right, key);}else if (key < root->_key){return _FindR(root->_left, key);}else{return true;}}

递归插入函数

bool InsertR(const K& key){return _InsertR(_root, key);}private:bool _InsertR(pNode& root, const K& key){if (!root){root = new Node(key);return true;}if (key > root->_key){return _InsertR(root->_right, key);}else if (key < root->_key){return _InsertR(root->_left, key);}else{return false;}}

pNode& root下面来展开讲讲为什么，这里用引用。我们都知道，引用是一个变量的别名，在这里就是表示上一个节点的左右指针的别名。那么当其左右指针为空时，我们可以直接new一个新的节点，再让其指向它。也就是相当于正常迭代中父节点的作用了。

递归删除节点

bool eraseR(const K& key){return _eraseR(_root, key);}private:bool _eraseR(pNode& root, const K& key){if (!root) return false;if (key > root->_key){return _eraseR(root->_right, key);}else if (key < root->_key){return _eraseR(root->_left, key);}else{pNode tmp = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{pNode leftnode = root->_right;while (leftnode->_left){leftnode = leftnodeo->_left;}swap(root->_key, leftnode->_key);return _eraseR(root->_right, key);}delete tmp;return true;}}

					while (leftnode->_left){leftnode = leftnodeo->_left;}swap(root->_key, leftnode->_key);return _eraseR(root->_right, key);

此次调用_eraseR的目的，把当前节点的右子树传给函数，再此时调用的函数中，利用其内部的删除度为1和0的功能把节点删除。算的上是一种功能的复用了。

删除根节点没问题，那么大概就没有问题了。

全代码

#include <iostream>
using namespace std;
template <class K>
struct BSTNode
{BSTNode(const K& key = K()):_left(nullptr),_right(nullptr),_key(key){}BSTNode<K>* _left;BSTNode<K>* _right;K _key;
};
template <class K>
class BSTree
{typedef BSTNode<K> Node;typedef Node* pNode;
public:BSTree()//构造:_root(nullptr){}~BSTree()//销毁{}pNode Find(const K& key){if (!_root) return nullptr;pNode cur = _root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return cur;}}return nullptr;}//插入bool Insert(const K& key = K()){if (!_root){_root = new Node(key);return true;}pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (key > parent->_key){parent->_right = cur;}else if (key < parent->_key){parent->_left = cur;}return true;}//删除bool erase(const K& key = K()){pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{//找到了if (cur->_left == nullptr)//度为0或者度为1，因为两种删除方法可以重和。所以写在一起{if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;return true;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else {if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_right;}}delete cur;return true;}else//度为2的节点{pNode NodeParent = cur;pNode leftnode = cur->_right;while (leftnode->_left)//找到最左边的节点{NodeParent = leftnode;leftnode = leftnode->_left;}cur->_key = leftnode->_key;//因为leftnode为要删除的位置，所以可以直接给cur赋值if (leftnode == NodeParent->_left)NodeParent->_left = leftnode->_right;elseNodeParent->_right = leftnode->_right;delete leftnode;return true;}}}return false;}//打印，中序递归遍历void Print(){_Print(_root);cout << endl;}bool FindR(const K&key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool eraseR(const K& key){return _eraseR(_root, key);}private:bool _eraseR(pNode& root, const K& key){if (!root) return false;if (key > root->_key){return _eraseR(root->_right, key);}else if (key < root->_key){return _eraseR(root->_left, key);}else{pNode tmp = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{pNode leftnode = root->_right;while (leftnode->_left){leftnode = leftnode->_left;}swap(root->_key, leftnode->_key);return _eraseR(root->_right, key);}delete tmp;return true;}}bool _InsertR(pNode& root, const K& key){if (!root){root = new Node(key);return true;}if (key > root->_key){return _InsertR(root->_right, key);}else if (key < root->_key){return _InsertR(root->_left, key);}else{return false;}}bool _FindR(pNode root, const K& key){if (!root) return false;if (key > root->_key){return _FindR(root->_right, key);}else if (key < root->_key){return _FindR(root->_left, key);}else{return true;}}private:void _Print(pNode root){if (root == nullptr){return;}_Print(root->_left);cout << root->_key << " ";_Print(root->_right);}private:pNode _root;
};