[C/C++] -- 二叉树-编程知识

1.简介

二叉树是一种每个节点最多有两个子节点的树结构，通常包括：根节点、左子树、右子树。

满二叉树：

如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。深度为k，有2^k - 1个节点。

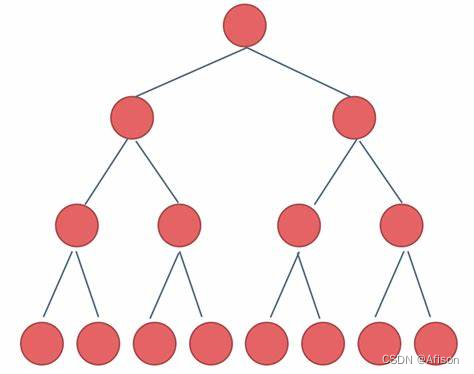
完全二叉树

除了最底层节点可能没填满外，其余每层节点数都达到最大值，且最下面一层节点都集中在该层最左边若干位置。若最底层为k层，则该层包含1~2^(k-1)个节点。

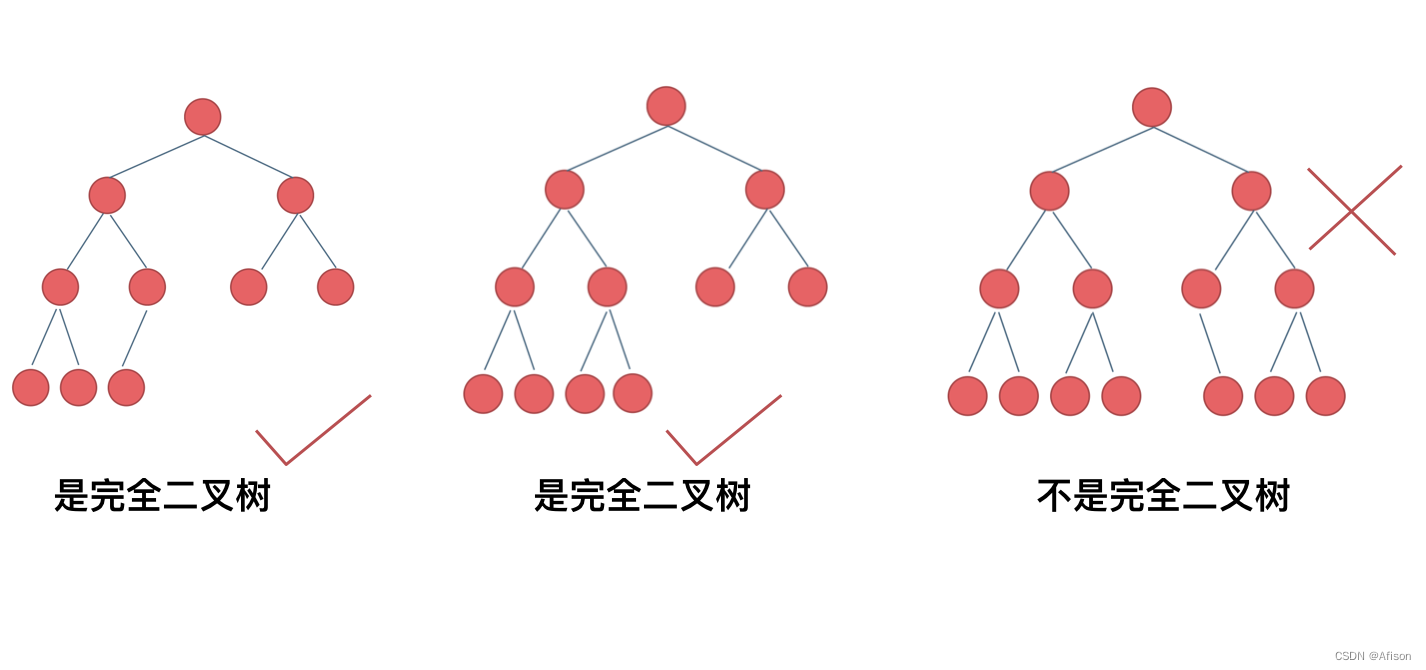
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

二叉搜索树有数值，是一个有序树。

若左子树不空，则左子树上所有节点值均小于根节点值。

若右子树不空，则右子树上所有节点值均大于根节点值。

左右子树分别为二叉搜索树

平衡二叉搜索树

任意节点的左子树和右子树高度差不超过1，空树仅有一个节点，也是一种平衡二叉搜索树

C++种map、set、multimap、multiset的底层实现是平衡二叉搜索树(红黑树)，所以增删时间复杂度O(logn)，unordered_map、unordered_set底层实现是哈希表，理想情况具有O(1)的增删时间复杂度，最坏情况O(n)。

二叉树存储方式

链式存储(指针)、顺序存储(数组)

二叉树定义：

#include <iostream>// 定义二叉树节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};int main() {// 创建二叉树节点TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);// 访问二叉树节点的数值std::cout << "The value of the root node is: " << root->val << std::endl;std::cout << "The value of the left child of the root is: " << root->left->val << std::endl;// 释放二叉树节点的内存delete root->left->left;delete root->left->right;delete root->left;delete root->right;delete root;return 0;
}

2.二叉树遍历

常用于图论：

深度优先遍历：先往深走、遇到叶子节点再往回走。(前序、中序、后续遍历：递归法、迭代法)

广度优先遍历：一层一层的去遍历。（层次遍历：迭代法）

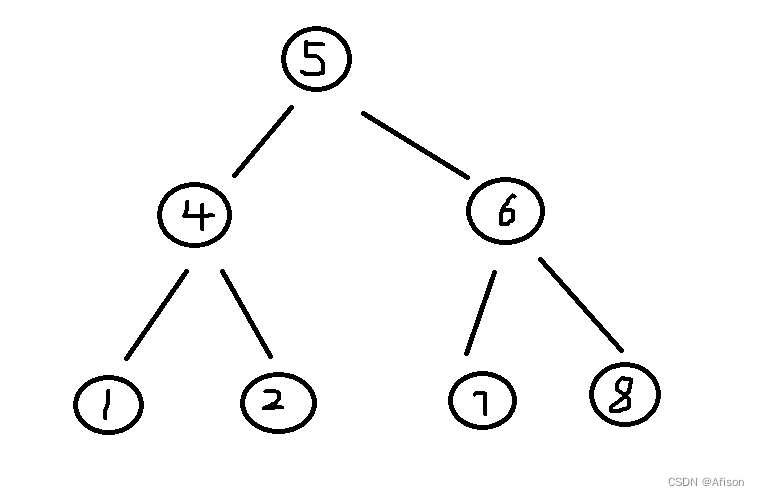
前中后指的是中间节点遍历顺序

前序：中左右 5 4 1 2 6 7 8

中序：左中右 1 4 2 5 7 6 8

后序：左右中 1 2 4 7 8 6 5

递归法：

前序遍历：

class Solution {public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val);traversal(cur->left,vec);        traversal(cur->right,vec);}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};

中序遍历：

class Solution {public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left,vec);vec.push_back(cur->val);        traversal(cur->right,vec);}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};

后序遍历：

class Solution {public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left,vec);        traversal(cur->right,vec);vec.push_back(cur->val);}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};

迭代法：

前序遍历

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;st.push(root);while (!st.empty()){TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->right) st.push(node->right);if (node->left) st.push(node->left);}return result;}
};

中序遍历

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;TreeNode* cur = root;while (cur != NULL || !st.empty()){if (cur != NULL){st.push(cur);cur = cur->left;}else{cur = st.top();st.pop();result.push_back(cur->val);cur = cur->right;}}return result;}
};

后序遍历

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()){TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left);if (node->right) st.push(node->right);}reverse(result.begin(),result. End());return result;}
};

3.例题

示例 1：

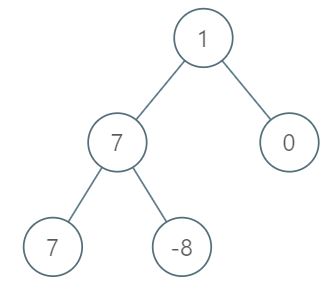
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2

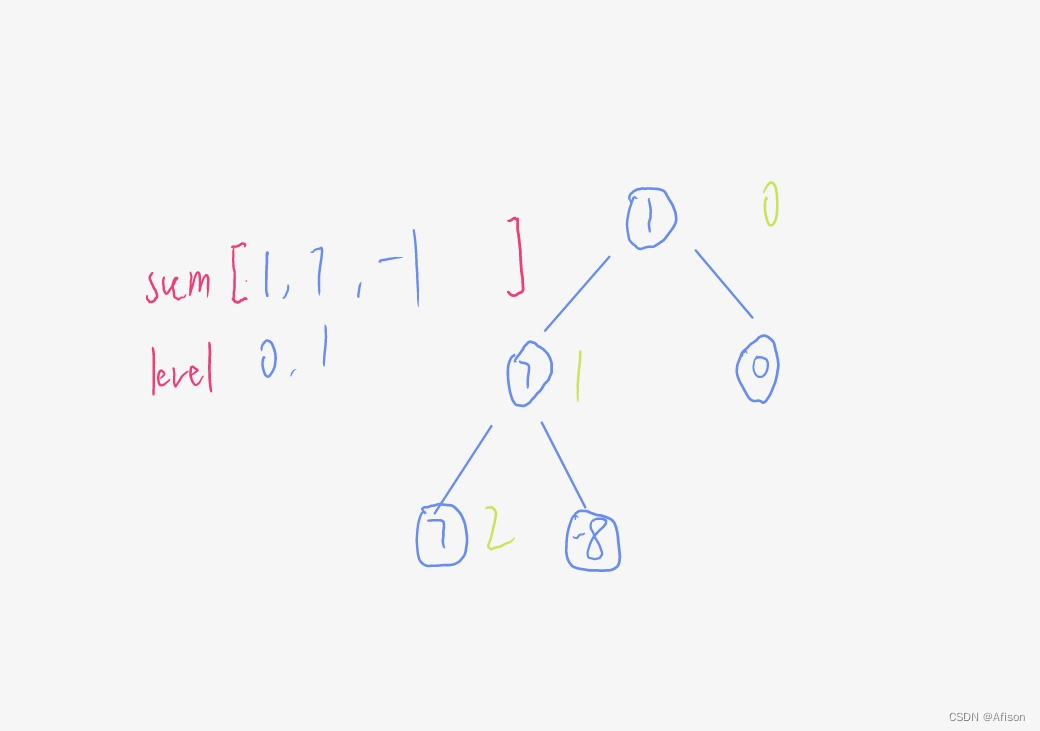
深度优先搜索

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {vector<int> sum;void dfs(TreeNode* node,int level){if(sum.size() == level){sum.push_back(node->val);}else{sum[level]+=node->val;}if(node->left){dfs(node->left,level+1);}if(node->right){dfs(node->right,level+1);}}public:int maxLevelSum(TreeNode* root) {dfs(root,0);int ans = 0;for(int i = 0;i<sum.size();i++){if(sum[i]>sum[ans]){ans = i;}}return ans+1;}
};

广度优先搜索

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxLevelSum(TreeNode* root) {int ans = 1,maxSum = root->val;vector<TreeNode*q> = {root};for(int level = 1;!q.empty();++level){vector<TreeNode*> nq;int sum = 0;for (auto node:q) {sum +=node->val;if (node->left){//用于在容器尾部直接构造一个新元素，可以避免额外的拷贝或移动操作。nq.emplace_back(node->left);}if(node->right){nq.emplace_back(node->right);}}if (sum > maxSum) {maxSum = sum;ans = level;}//通过 move(nq)，我们将 nq 的所有权（ownership）转移给 q。//这意味着实际上并不会进行元素的复制，而是直接将 nq 中的元素转移到 q 中，同时 nq 被置为空。q = move(nq);}return ans;}
};