本文是自己在学习Numpy过后总是遗忘的很快,反思后发现主要是两个原因:
- numpy的知识点很多,很杂乱。
- 练习不足,学习过后一段时间不敲代码就会忘记。
针对这两个问题,我写了这篇文章。希望将numpy的知识点织成一张网,形成一个体系。能够方便我每次复习的时候快速回想,并帮助我构建对知识点之间的关联,巩固和加深理解。
一、Numpy知识点体系
这里的知识体系我是只给出了提示信息,没有具体到知识点。这样在复习Numpy的时候,可以参考下面的内容,看看自己能否回答出正确的知识点。然后下面的思维导图里有正确答案,检查自己还有哪些知识点记得不清。
(1)创建数组
① 6种常用创建的方式
② 4种随机创建的方式
③ 3种按范围创建的方式
④ 7种从已有数组中创建的方式
(2)数组属性
① 维度
② 形状
③ 大小
④ 数据类型
(3)操作数组
① 重塑与转置
② 级联与分割
③ 数组的运算
④ 索引与切片
⑤ 统计分析函数
⑥ 副本
二、Numpy知识点体系(思维导图形式)
【腾讯文档】Numpy复习手册 ![]() https://docs.qq.com/mind/DY2lRbmdGV0JRT0xy
https://docs.qq.com/mind/DY2lRbmdGV0JRT0xy
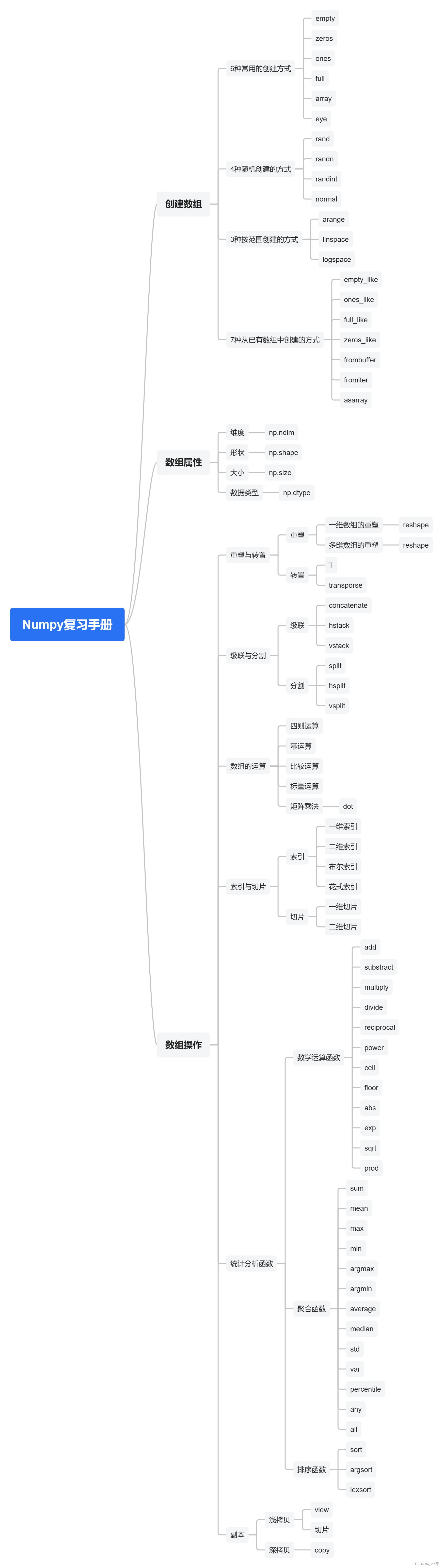
思维导图