Leetcode 第 389 场周赛题解

题目1：3083. 字符串及其反转中是否存在同一子字符串

思路

代码

/** @lc app=leetcode.cn id=3083 lang=cpp** [3083] 字符串及其反转中是否存在同一子字符串*/// @lc code=start
class Solution
{
public:bool isSubstringPresent(string s){int n = s.length();for (int i = 0; i < n - 1; i++){string t1 = s.substr(i, 2);for (int j = n - 1; j > 0; j--){string t2 = s.substr(j - 1, 2);reverse(t2.begin(), t2.end());if (t1 == t2)return true;}}return false;}
};
// @lc code=end

复杂度分析

时间复杂度：O(n²)，其中 n 是字符串 s 的长度。

空间复杂度：O(1)。

题目2：3084. 统计以给定字符开头和结尾的子字符串总数

思路

假设字符串 s 中有 count 个字符 c。

第一个字符 c 可以和后面 count-1 个 字符 c 组成以 c 字符开头和结尾的非空子字符串。

第二个字符 c 可以和后面 count-2 个 字符 c 组成以 c 字符开头和结尾的非空子字符串。

以此类推。

所以以 c 字符开头和结尾的非空子字符串的总数为 (count-1) + (count-2) + … + 1 = count * (count+1) / 2。

代码

/** @lc app=leetcode.cn id=3084 lang=cpp** [3084] 统计以给定字符开头和结尾的子字符串总数*/// @lc code=start
class Solution
{
public:long long countSubstrings(string s, char c){long long count = 0;for (char &ch : s)if (ch == c)count++;// long long ans = 0;// for (int i = 1; i <= count; i++)//     ans += i;// return ans;return count * (count + 1) / 2;}
};
// @lc code=end

复杂度分析

时间复杂度：O(n)，其中 n 是字符串 s 的长度。

空间复杂度：O(1)。

题目3：3085. 成为 K 特殊字符串需要删除的最少字符数

思路

类似于滑动窗口。

统计好字符的出现次数后，排序，遍历这个数组，假设当前值为 f，则频率的上界为 f+k。

统计频率为 [f, f+k] 的总字符个数，维护其最大值 max_save，那么最少删除个数就是字符串长度 word.length() - max_save。

代码

/** @lc app=leetcode.cn id=3085 lang=cpp** [3085] 成为 K 特殊字符串需要删除的最少字符数*/// @lc code=start
class Solution
{
public:int minimumDeletions(string word, int k){unordered_map<char, int> mp;for (char &c : word)mp[c]++;vector<int> freq;for (auto &[ch, cnt] : mp)freq.push_back(cnt);sort(freq.begin(), freq.end());int min_del = INT_MAX;int front_sub = 0; // 前置差用来存储较小，并且需要减去的数for (int &f : freq){int upper = f + k;int back_sub = 0; // 后置差用来存储后面较大数据需要减去的数for (int &j : freq)if (j > upper)back_sub += j - upper;min_del = min(min_del, front_sub + back_sub);// 如果以后面一个大一点的数为最小值，此时前置差就得加上当前这个数front_sub += f;}return min_del;}
};
// @lc code=end

复杂度分析

时间复杂度：O(n+∣Σ∣)，其中 n 是字符串 word 的长度，∣Σ∣ 为字符集合的大小，本题字符均为小写字母，所以 ∣Σ∣=26。

空间复杂度：O(∣Σ∣)，其中 ∣Σ∣ 为字符集合的大小，本题字符均为小写字母，所以 ∣Σ∣=26。

题目4：3086. 拾起 K 个 1 需要的最少行动次数

思路

动作 1：在一个空位上生成一个 1。这个动作最多可以执行 maxChanges 次。
动作 2：把一个 1 移动到相邻的空位上。

动作 1 + 动作 2 = 在Alice相邻的空位上生成一个 1，再交换给Alice，花费为 2。

我们给Alice选初始位置时，最好选择 1 聚集的地方，具体来讲 1、1（Alice）、1 是比较好的。

这是一个货仓选址问题。

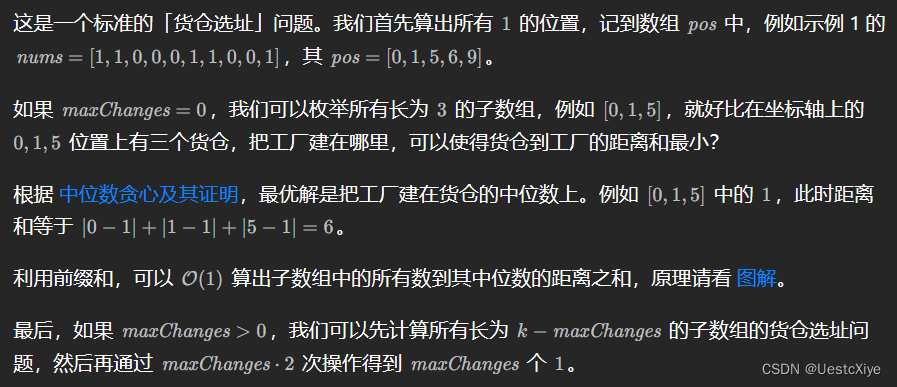
代码

/** @lc app=leetcode.cn id=3086 lang=cpp** [3086] 拾起 K 个 1 需要的最少行动次数*/// @lc code=start
class Solution
{
public:long long minimumMoves(vector<int> &nums, int k, int maxChanges){vector<int> pos;int c = 0; // nums 中连续的 1 长度for (int i = 0; i < nums.size(); i++){if (nums[i] == 0)continue;pos.push_back(i); // 记录 1 的位置c = max(c, 1);if (i > 0 && nums[i - 1] == 1){if (i > 1 && nums[i - 2] == 1){ // 有 3 个连续的 1c = 3;}else{ // 有 2 个连续的 1c = max(c, 2);}}}c = min(c, k);if (maxChanges >= k - c){// 其余 k-c 个 1 可以全部用两次操作得到return max(c - 1, 0) + (k - c) * 2;}int n = pos.size();vector<long long> preSum(n + 1);for (int i = 0; i < n; i++)preSum[i + 1] = preSum[i] + pos[i];long long ans = LLONG_MAX;// 除了 maxChanges 个数可以用两次操作得到，其余的 1 只能一步步移动到 pos[i]int size = k - maxChanges;for (int right = size; right <= n; right++){// s1+s2 是 j 在 [left, right) 中的所有 pos[j] 到 index=pos[(left+right)/2] 的距离之和int left = right - size;int i = left + size / 2;long long index = pos[i];long long s1 = index * (i - left) - (preSum[i] - preSum[left]);long long s2 = preSum[right] - preSum[i] - index * (right - i);ans = min(ans, s1 + s2);}return ans + maxChanges * 2;}
};
// @lc code=end

复杂度分析

时间复杂度：O(n)，其中 n 是数组 nums 的长度。

空间复杂度：O(n)，其中 n 是数组 nums 的长度。