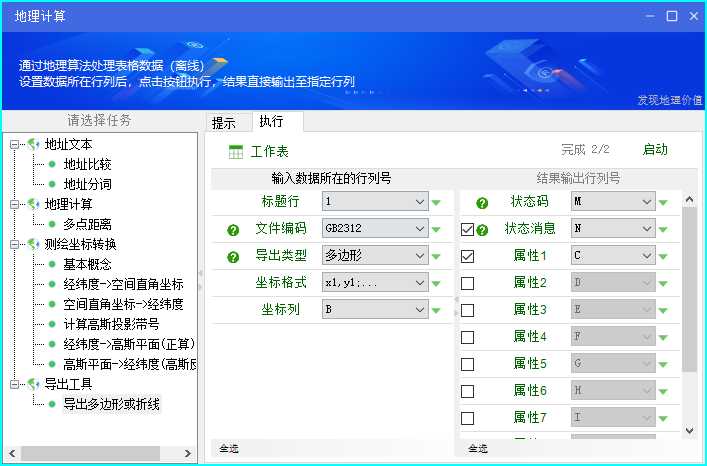
生日问题
我的小学同班同学小琦,和我是同一天生日。每次聚会,我俩同时在场时,我们都会向其他人提起这一点。我们觉得这是很幸运的。
这个概率大吗?要回答这样的问题,需要把几个问题区分清楚。
- 问题1:对于特定的某个同学,他与我生日相同的概率是多少?这个概率是1/365,并不大。
- 问题2:某班有𝑆个学生,有人与我生日相同的概率是多少?这个概率大约是(𝑆-1)/365,并不小。
- 问题3:某班有𝑆个学生,至少两个学生生日相同(月和日相同)的概率是多少?
问题3是概率中的生日问题(Birthday Problem)。首先,计算没有人生日相同的概率。为了表达式的含义更明确,用𝐴表示一年的天数365。所有人生日不同的概率为:
P = A ( A − 1 ) ( A − 1 ) . . . ( A − S + 1 ) A S . P = \frac {A(A-1)(A-1) ... (A-S+1)} {A^S}. P=ASA(A−1)(A−1)...(A−S+1).
至少有两人生日相同的概率为1−𝑃。下图绘制了至少两人生日相同的概率(纵坐标)与人数(横坐标)的关系。如果班里有23人,至少有两人生日相同的概率>50%;如果有57人,概率>99%。
如果要和人打赌一个班有没有相同生日的人,只要人数不少于23人,就可以赌有,获胜的概率超过一半。

还有另一个问题。令𝑋表示班里生日相同的对数。𝑋的期望是多少?
E ( X ) = S ( S − 1 ) 2 1 A . E(X) = \frac {S(S-1)} 2 \frac 1 A. E(X)=2S(S−1)A1.
生物特征识别也有生日问题。在生物特征系统中,一个人被编码为其的生物特征,例如人像、指纹、虹膜。如果生物特征识别算法认为两个人的生物特征重了,就是发生了错误匹配(False Match)。任意一对生物特征的错误匹配概率(FMR,False Match Rate),类似任意两个人的生日相同概率(1/A)。只要有两个人的生物特征重了,就叫做发生冲突。假设整个系统一共有𝑆人,识别算法的FMR需要多小,才能使冲突概率约为1/2?
不冲突的概率为:
( 1 − F M R ) S ( S − 1 ) 2 = 0.5 (1-FMR)^{\frac {S(S-1)} 2} = 0.5 (1−FMR)2S(S−1)=0.5
得出:
F M R = 1 − 0. 5 2 S ( S − 1 ) FMR = 1-0.5^ {\frac 2 {S(S-1)}} FMR=1−0.5S(S−1)2
下图绘制了FMR和𝑆的关系,由于两个数字的范围都太大,用对数坐标。从中看出,有1亿人时,冲突概率1/2对应的FMR为 1 0 − 16 10^{-16} 10−16。

生物特征冲突在大规模身份识别系统中容易出现。因此,大规模身份识别系统对于FMR要求非常高。例如,印度曾经没有全民的身份证,有人根本没有身份,而有人有多重身份,这会带来很多社会问题。后来印度实施了Aadhaar项目,要给每个印度人一个唯一的身份证。印度有14亿多人口,为了保证尽可能低的FMR(因此尽可能低的冲突概率),采集了每个人的人像、十指指纹和一对虹膜。
每当有人来申请身份证,要在所有已经发证的数据库中,进行生物特征查重。当所有人的身份证都办完的时候,14亿人之间就全部做过比对了。一共是 2 × 1 0 18 2 \times 10^{18} 2×1018,200亿亿次比对。这就要求FMR要非常低。

为了降低FMR,Aadhaar项目融合了三种生物特征。实验表明,指纹加虹膜的效果特别有效。在一个大规模的测试库上,融合后的错误率显著下降。

参考文献
-
A.K. Jain. http://biometrics.cse.msu.edu/Presentations/MBZUAI_Sept_1_2020.pdf
-
Daugman, John. “Collision avoidance on national and global scales: Understanding and using big biometric entropy.” TechRxiv (2021).