第五章 深度学习
二、推荐系统
3. 关联规则
3.1 Apriori
“啤酒与尿布”的故事产生于 20 世纪 90 年代的美国沃尔玛超市。沃尔玛的超市管理人员分析销售数据时发现了一个令人难于理解的现象:在某些特定的情况下,“啤酒”与“尿布”两件看上去毫无关系的商品会经常出现在同一个购物篮中,这种独特的销售现象引起了管理人员的注意,经过后续调查发现。原来,美国的妇女通常在家照顾孩子,所以她们经常会嘱咐丈夫在下班回家的路上为孩子买尿布,而丈夫在买尿布的同时又会顺手购买自己爱喝的啤酒。这样就会出现啤酒与尿布这两件看上去不相干的商品经常会出现在同一个购物篮的现象。
这个发现为商家带来了大量的利润,但是如何从浩如烟海却又杂乱无章的数据中,发现啤酒和尿布销售之间的联系呢?
3.1.1 Apriori 算法产生
1993 年美国学者 Agrawal 提出通过分析购物篮中的商品集合,从而找出商品之间关联关系的关联算法,并根据商品之间的关系,找出客户的购买行为。Agrawal 从数学及计算机算法角度提出了商品关联关系的计算方法——Apriori 算法。
沃尔玛从上个世纪 90 年代尝试将 Aprior 算法引入到 POS 机数据分析中,并获得了成功,于是产生了“啤酒与尿布”的故事。
3.1.2 如何寻找?
在历史购物记录中,一些商品总是在一起购买。但人看上去不是那么的直观的,而是隐蔽的。让计算机做这事,设计算法让计算机自动去找,找到这样的模式(规律)。
目标:寻找那些总是一起出现商品。
mahout 实战—>机器学习实战
《mahout 实战》与《机器学习实战》一起购买的记录数占所有商品记录总数的比例——支持度(整体)
买了《mahout 实战》与《机器学习实战》一起购买的记录数占所有购买《mahout 实战》记录数的比例——置信度(局部)
需要达到一定的阈值
支持度、置信度越大,商品出现一起购买的次数就越多,可信度就越大。
支持度:在所有的商品记录中有 2%量是购买《mahout 实战》与《机器学习实战》
置信度:买《mahout 实战》的顾客中有 60%的顾客购买了《机器学习实战》
作用:找到商品购买记录中反复一起出现的商品,能帮助营销人员做更好的策略,帮助顾客方便购买。
策略:
1、同时购买的商品放一起
2、同时购买的商品放两端
支持度、置信度转化为数学语言进行计算:
A 表示《mahout 实战》B 表示《机器学习实战》
support(A->B) = P(AB) (《mahout 实战》和《机器学习实战》一起买占总的购买记录的比例)
confidence(A->B) = P(B|A) (购买了《mahout 实战》后,买《机器学习实战》占的比例)
项集:项的集合称为项集,即商品的组合。
k 项集:k 件商品的组合,不关心商品件数,仅商品的种类。
项集频率:商品的购买记录数,简称为项集频率,支持度计数。
注意,定义项集的支持度有时称为相对支持度,而出现的频率称为绝对支持度。
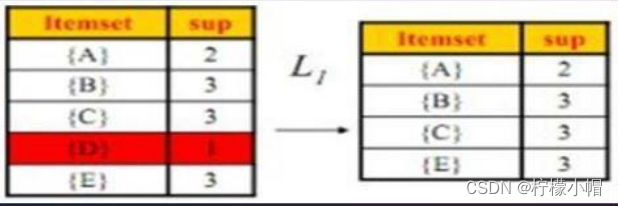
频繁项集:如果项集的相对支持度满足给定的最小支持度阈值,则该项集是频繁项集。
强关联规则:满足给定支持度和置信度阈值的关联规则。

3.1.3 明确问题
要找总是在一起出现的商品组合
提出衡量标准支持度、置信度(达到一定的阈值)
给出支持度、置信度直观计算方法
在计算方法中起决定因素的是频繁项集
由频繁项集轻松找到强关联规则
找关联规则 --> 找频繁项集
步骤:
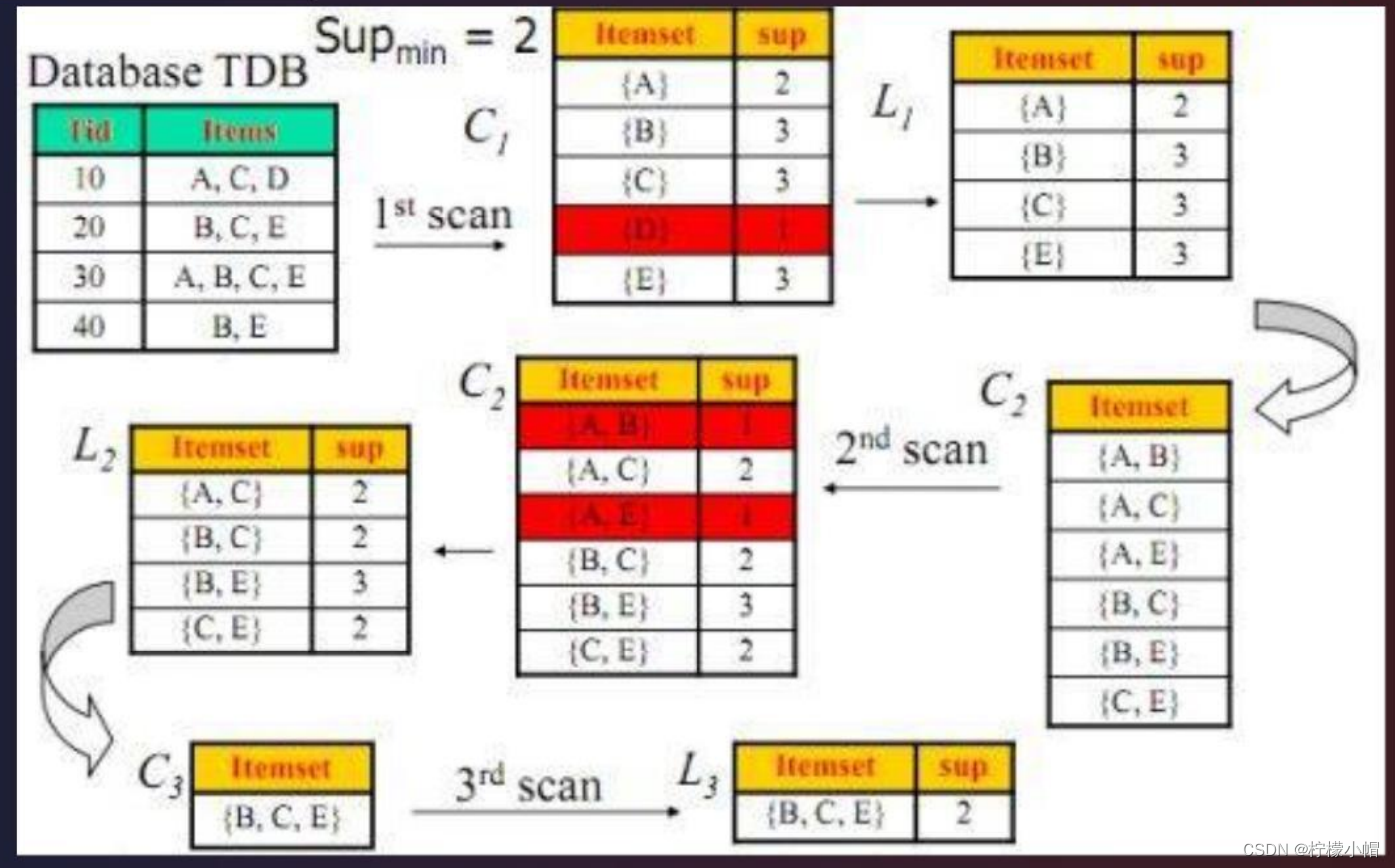
- 找出所有的频繁项集;这个项集出现的次数至少与要求的最小计数一样。如在 100 次购买记录中,至少一起出现。
- 由频繁项集产生强关联规则;这些关联规则满足最小支持度与最小置信度。
先验性质:频繁项集的所有非空子集也一定是频繁的。
逆否命题:若一个项集是非频繁的,则它的任何超集也是非频繁的。
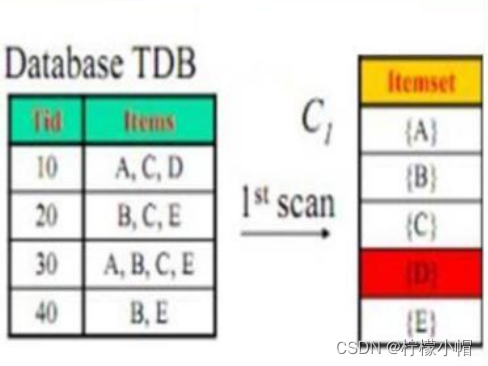
3.1.4 挑战
-
多次数据库扫描
-
巨大数量的候补项集
-
繁琐的支持度计算
3.1.5 改善 Apriori: 基本想法
- 减少扫描数据库的次数
- 减少候选项集的数量
- 简化候选项集的支持度计算
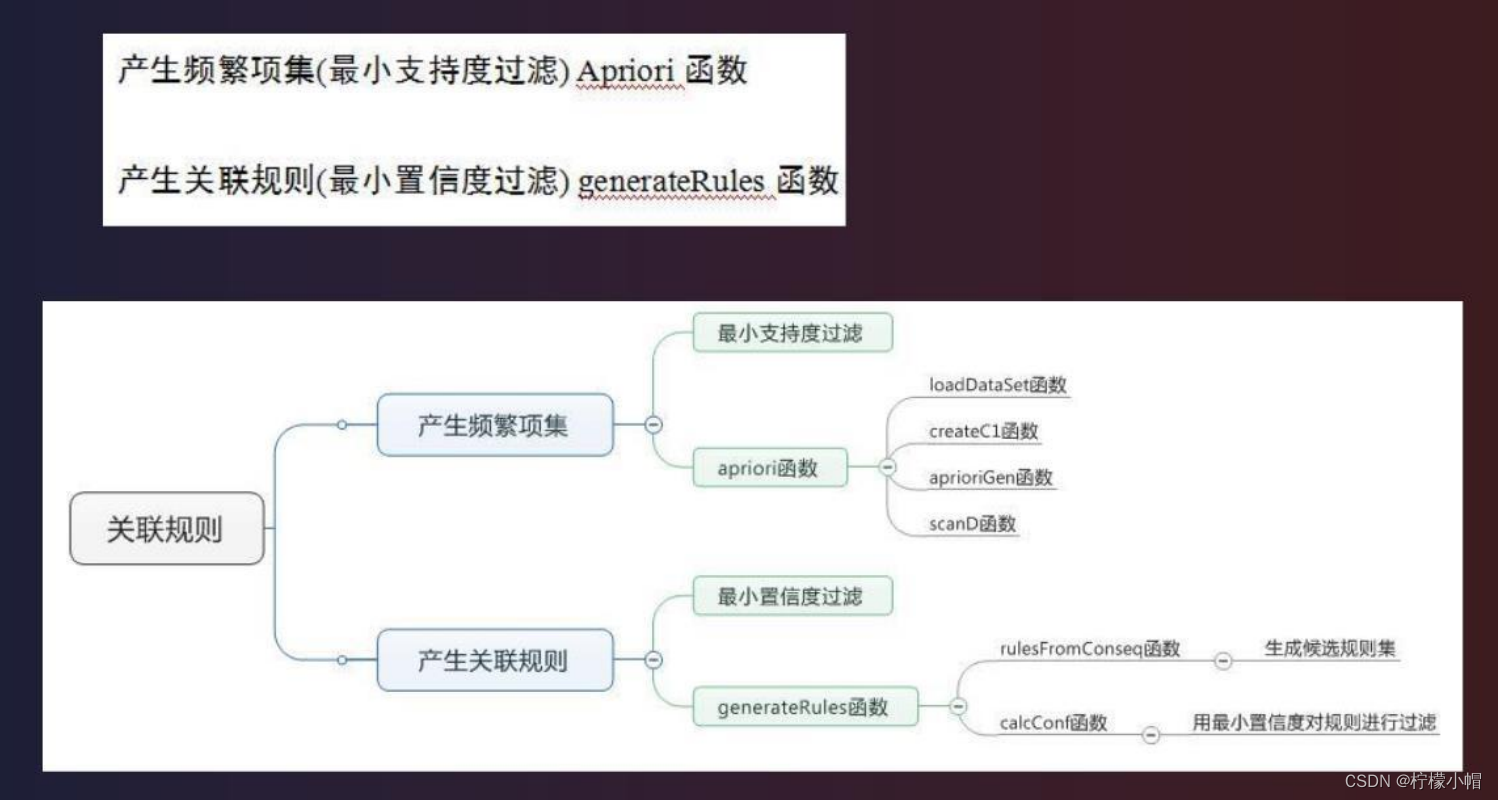
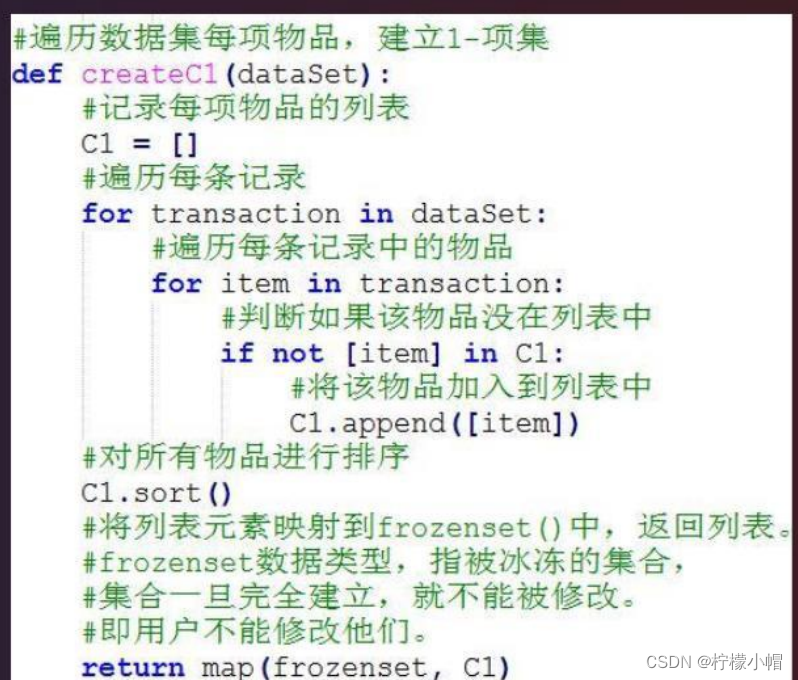
3.1.6 代码
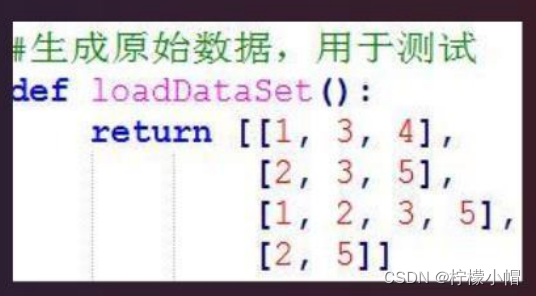



3.2 FPGrowth
相比 Apriori 算法需要多次扫描数据库,FPGrowth 只需要对数据库
扫描 2 次。
第 1 次扫描获得单个项目的频率,去掉不满足支持度要求的项,并对剩下的项排序。
第 2 次扫描建立一颗 FP-Tree 树。
3.2.1 例子
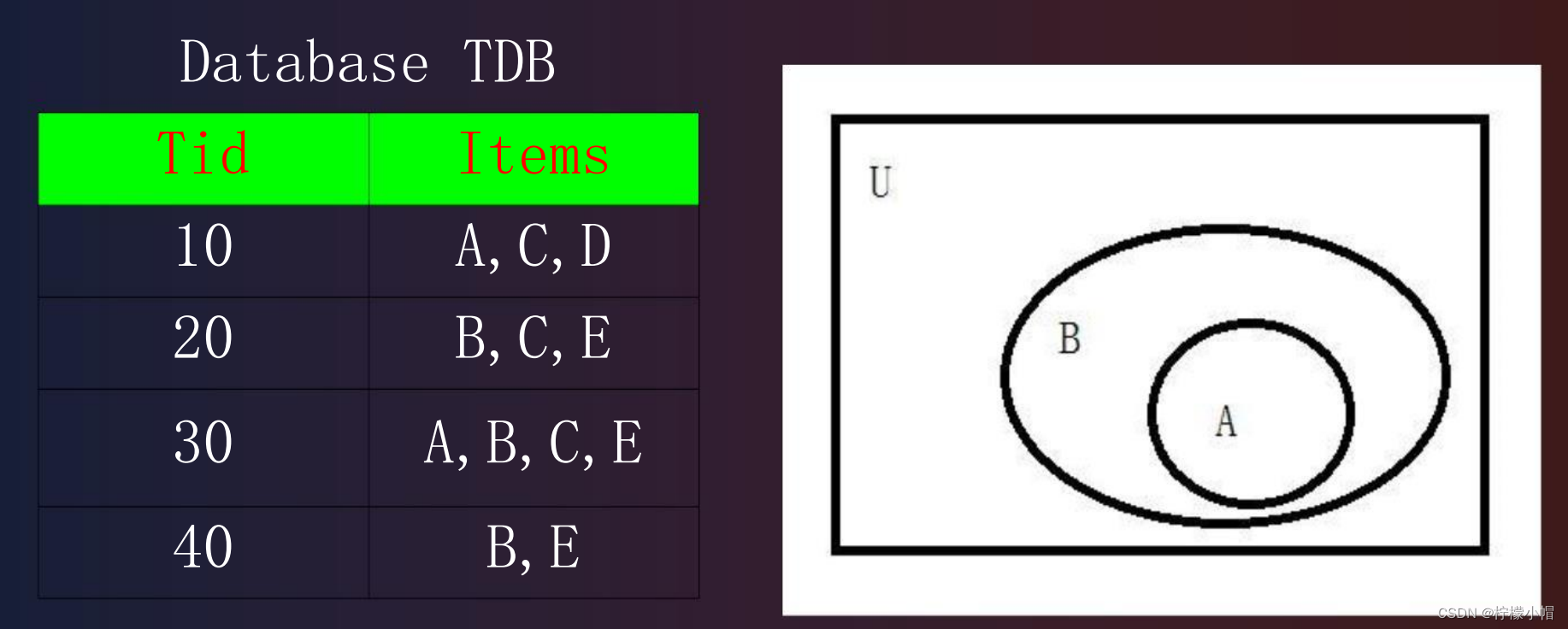
| ID | Items |
|---|---|
| 1 | A,E,F,G |
| 2 | A,F,G |
| 3 | A,B,E,F,G |
| 4 | E,F,G |
{A,F,G}的支持度数为 3,支持度为 3/4。
{F,G}的支持度数为 4,支持度为 4/4。
{A}的支持度数为 3,支持度为 3/4。
{F,G}=>{A}的置信度为:{A,F,G}的支持度数除以{F,G}的支持度数,即 3/4
{A}=>{F,G}的置信度为:{A,F,G}的支持度数除以{A}的支持度数,即 3/3 4
挖掘强关联规则是在满足一定支持度的情况下寻找置信度达到阈值的所有商品组合。
3.2.2 规律
我们要找出哪些总是一起购买的商品,比如人们买薯片的时候通
常也会买鸡蛋,则[薯片,鸡蛋]就是一条频繁模式(规律)。
第一步:扫描数据库,每项商品按频数递减排序,删除频数小于最小支持度 MinSup 的商品。 (第一次扫描数据库)
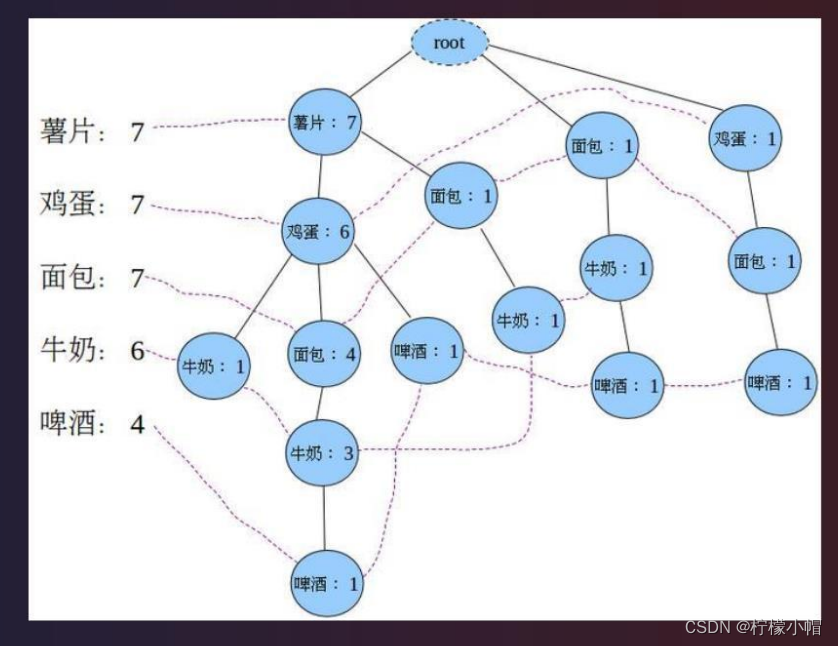
薯片:7 鸡蛋:7 面包:7 牛奶:6 啤酒:4 (这里我们令 MinSup=4)以上结果就是频繁 1 项集,记为 F1。
F1 中排序 薯片:7 鸡蛋:7 面包:7 牛奶:6 啤酒:4
第二步:对于每一条购买记录,按照 F1 中的顺序重新排序。
| ID | Items |
|---|---|
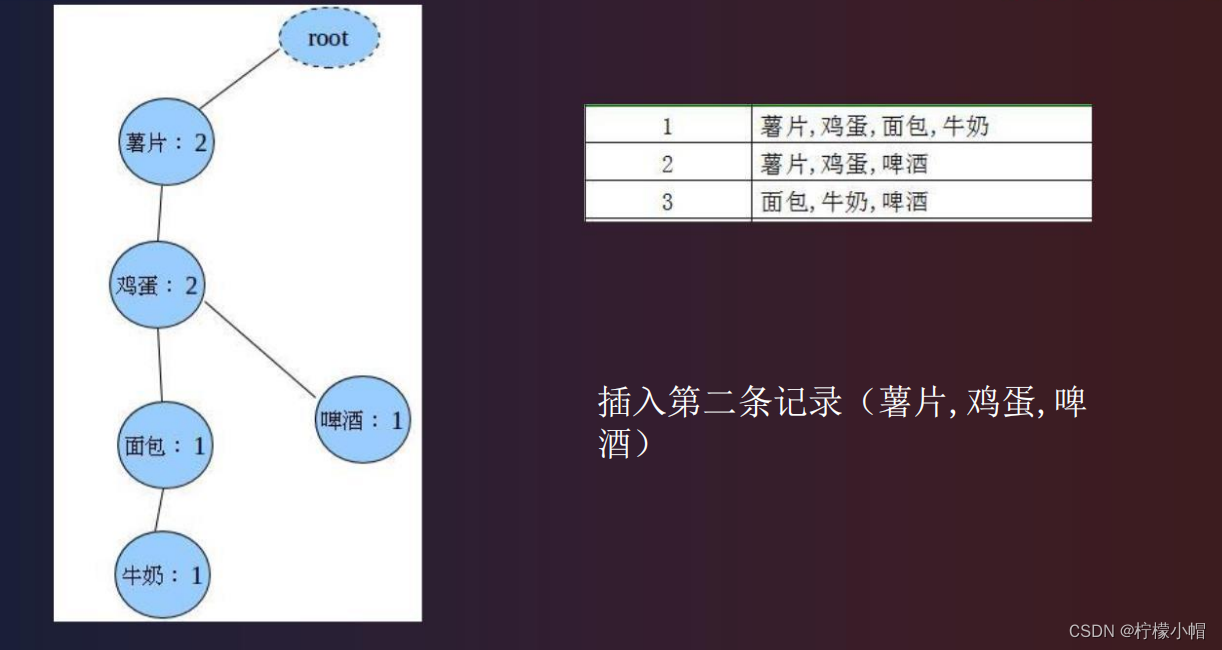
| 1 | 薯片,鸡蛋,面包,牛奶 |
| 2 | 薯片,鸡蛋,啤酒 |
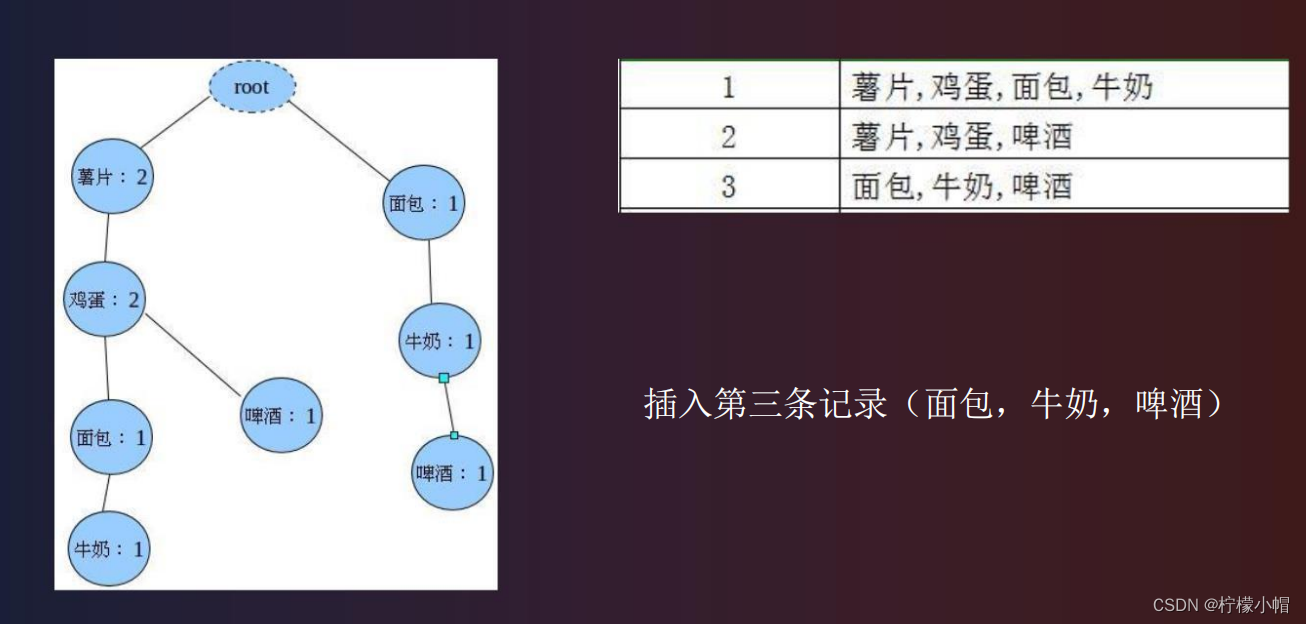
| 3 | 面包,牛奶,啤酒 |
| 4 | 薯片,鸡蛋,面包,牛奶,啤酒 |
| 5 | 薯片,鸡蛋,面包 |
| 6 | 鸡蛋,面包,啤酒 |
| 7 | 薯片,面包,牛奶 |
| 8 | 薯片,鸡蛋,面包,牛奶 |
| 9 | 薯片,鸡蛋,牛奶 |
第三步:把第二步得到的各条记录插入到 FP-Tree 中。