IVS模型解释-编程知识

核心思路

【Implied volatility surface predictability: The case of commodity markets】

半参数化模型：利用各种参数(或者因子)对隐含波动率进行降维（静态参数化因子模型），对参数化因子的时间序列进行间接的建模

基于非对称的二元多项式回归方程对每日的单个品种的隐含波动率面关于期限（maturity-\tao）和内在价值（moneyness-\delta）的关系进行刻画。（实现在值程度\delta的不对称）
在这里插入图片描述
为了完成一定的预测目标，在刻画单位时间段的隐含波动率面之后，我们假设参数服从AR、ARMA、VAR等过程，使用动态参数的办法完成对下一时刻隐含波动率面的预测。

一、数据生成

（1）get_opt_daily(exchange, object)处理原始数据成为包含行情和期权合约信息的数据，（原始数据包括了opt_day_data，mkt_optd），call、put转化为1和-1；存为opt_S_K_t.pkl；

频率降低：

通过 freq_reduce 方法对数据进行频率降低处理。
首先对数据进行排序，然后按照指定的时间间隔（time_gap）对数据进行分组汇总，例如每5分钟或者10分钟。
汇总方法为取每个时间段内的第一条记录的开盘价、最后一条记录的收盘价、最高价、最低价、成交量和成交额等指标。

（2）cal_IV.py 生成期权隐含波动率的数据iv_greeks_result.pkl；和上面的行情数据拼在一起组成了IVS_raw_data.pkl，这就包括了我们全部训练需要的数据；
（商品期权用二分法，ETF和股指用BS公式）

预处理：

1、剔除掉所有距到期日小于等于 7 个日历日的期权数据。（因为剩余期限过短的期权可能存在流动性问题，并且其包含的时间价值已经很少;）
2、剔除所有当天交易量少于 30 的期权数据，防止因为交易量过少导致的价格失真。
3、剔除与期权理论价格相悖的不合理数据，即实值期权价格超出理论价格上下限的数据。
4、剔除平值期权上下 5 档以外的期权合约，即部分过于实值与虚值的期权合约，5 档以内的期权合约流动性相对会比较好

央行一年期存款利率与一年期贷款利率的平均值作为无风险利率的估值

在值程度

在值程度是指期权的价内性(moneyness),也就是期权相对于行权价格的位置。 m=K/F-1(即 K/(S*e^r(T-t))-1)

定义call_put变量,表示期权类型。call_put=1表示看涨期权(call),call_put=-1表示看跌期权(put)
对于看涨期权:
- 如果标的价格obj_close高于行权价格exercise_price,期权处于价内实值,moneyness大于0
- 如果obj_close低于exercise_price,期权处于价外虚值,moneyness小于0
对于看跌期权:
- 如果obj_close低于exercise_price,期权处于价内实值,moneyness大于0
- 如果obj_close高于exercise_price,期权处于价外虚值,moneyness小于0
计算moneyness时乘以call_put变量,可以将看涨期权和看跌期权的价内性定义统一为大于0表示价内实值,小于0表示价外虚值。
将**标的价格与行权价格差额除以标的价格,可以将价内性定义在0到1之间,**更容易理解期权相对行权价格的位置。

对于看涨期权，当m < -0.06时为深度实值;-0.06 <m<-0.01时为实值;-0.01<m<0.01时为平值;0.01<m <0.06时为虚值;0.06m时为深度虚值

剔除的数据有:m<0的看涨期权;m>0的看跌期权。只对虚值期权与平值期权进行建模

平值附近分层

根据期权平价公式，看涨期权和看跌期权的隐含波动率应该相等，但是事实上，由于交易成本、卖空限制等因素，看涨与看跌期权的隐含波动率允许存在一定的偏差，在一个合理的偏差范围内。因此，为了下一步的研究，我们还需要对期权隐含波动率曲面进行平滑处理，以保证看涨期权和看跌期权隐含波动率的一致性。

我们知道，理论上不存在真正的平值合约，将同一剩余期限上离标的资产价格最近的行权价所对应的合约作为平值合约,并计算平值合约隐含波动率的差额(平值看涨期权隐含波动率-平值看跌期权隐含波动率)
将平值合约的隐含波动率调整为**(平值看涨期权隐含波动率+平值看跌期权隐含波动率)/2**
将同一期限的所有看跌期权隐含波动率+平值合约隐含波动率差额/2，所有看涨期权隐含波动率-平值合约隐含波动率差额/2，即把隐含波动率偏斜的两翼进行整体平移调整

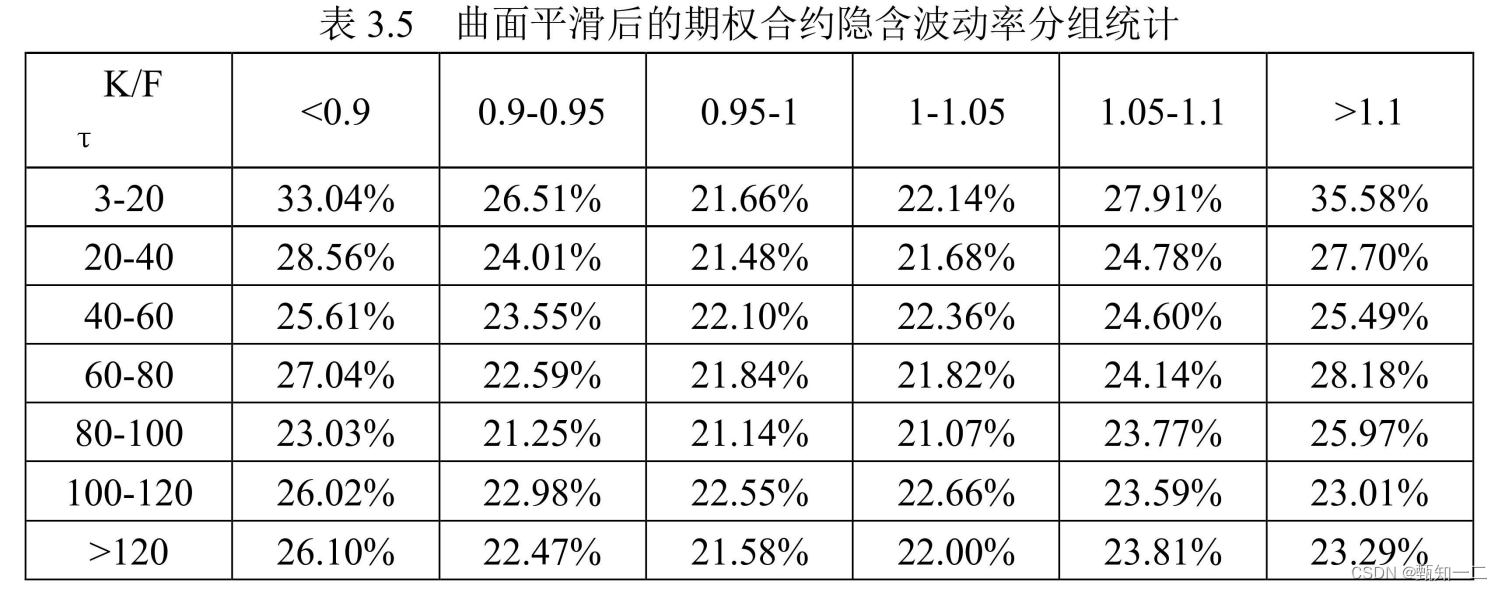
在这里插入图片描述

总结

1.对于同一剩余期限，波动率微笑的现象仍然存在，即偏离平值的期权隐含波动率高于平值期权，呈现微笑特征
2.几乎所有靠近平值的期权在不同剩余期限上都拥有比较稳定的隐含波动率，隐含波动率大致维持在22%左右
3.离到期日靠近且偏离平值程度大的期权往往都有更高的隐含波动率。

到期时间怎么计算（用自然日）

交易日定价法低估了节后第一个交易日的市场波动，自然日定价法则高估了节后第一个交易日的市场波动

自然日的方式考虑到了资金成本对期权价格的影响，并且认为假期后的第一个交易日的波动性会更强（例如周六、周日两个休息日后的周一的波动率在自然日算法中被认为是其他交易日波动率的1.732（即根号3）倍）
交易日方法没有考虑长假期间资金成本的影响，并且认为长假后交易日的波动率与其他交易日的波动率并没有什么异同。

但是考虑到使用单一方式定价时，交易日方法容易导致投资者严重忽视临近到期日的长假带来的合约价格下降，因此我们更建议投资者使用自然日的定价方法。

二、基于IVS方程的模型拟合与预测

（1）静态拟合过程（针对各个品种的期权数据，拟合波动率曲面，主要是方程中的6个IVS参数，还需要检验拟合的R方+RMSE等）
regression(data=data, obj=obj, trade_date=date, Lambda=1)
返回拟合的参数向量，以及R2；
estimation(obj_list=obj_list, raw_data=IV_raw_data)
返回所有品种每日的所有IVS方程参数，存储为result_df.csv；

有些规则可能长期适用，短期不一定适用，因此需要做长短期检验
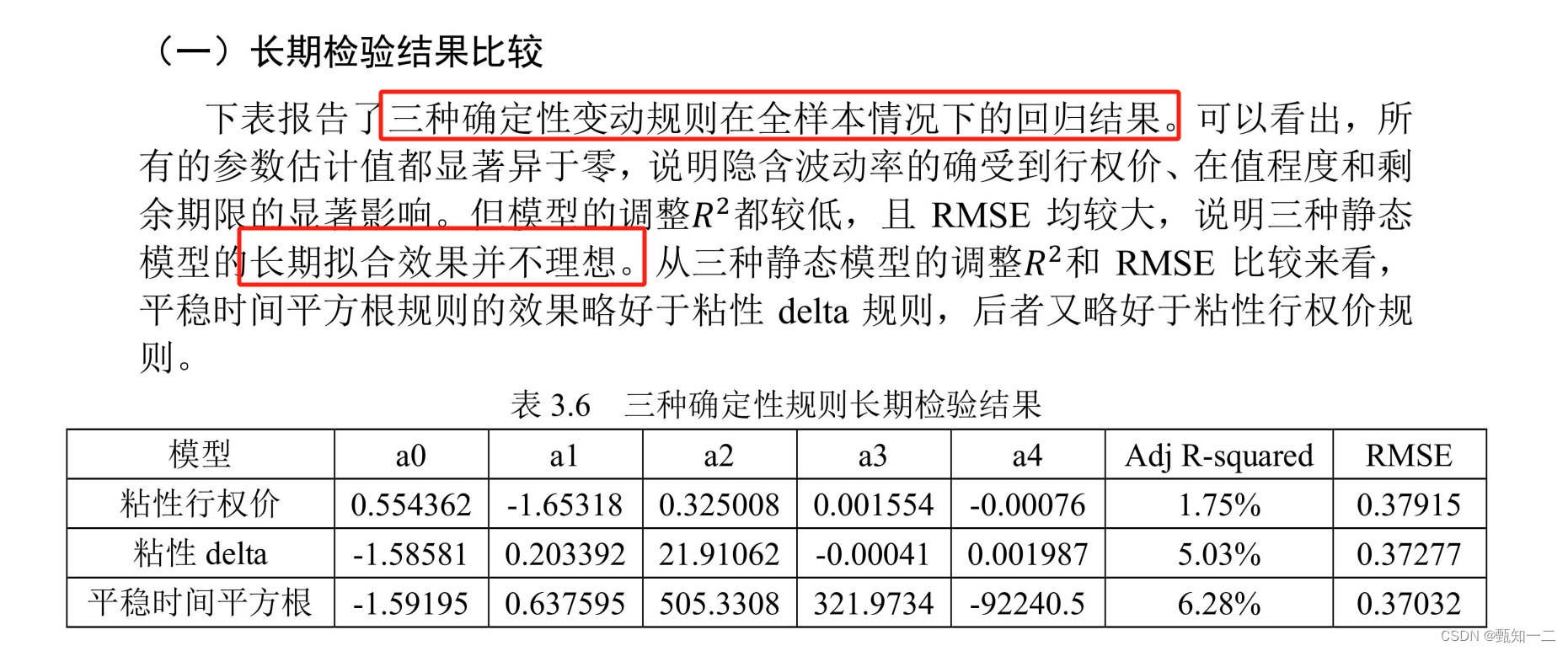
确定非对称二元多项式模型为使用的模型

根据下表可以明显看出，静态波动率建模非常不对，需要做动态预测
在这里插入图片描述

（2）动态预测过程（动态预测之后的6个参数向量）
beta_df = predict_beta(result_df, 20210601, obj_list)；
基于AR模型做动态参数预测，每日预测的参数向量beta，存为beta_df.csv；

做出多个系数的相关性系数图，系数之间存在相关关系，利用VAR模型反应因子动态关系
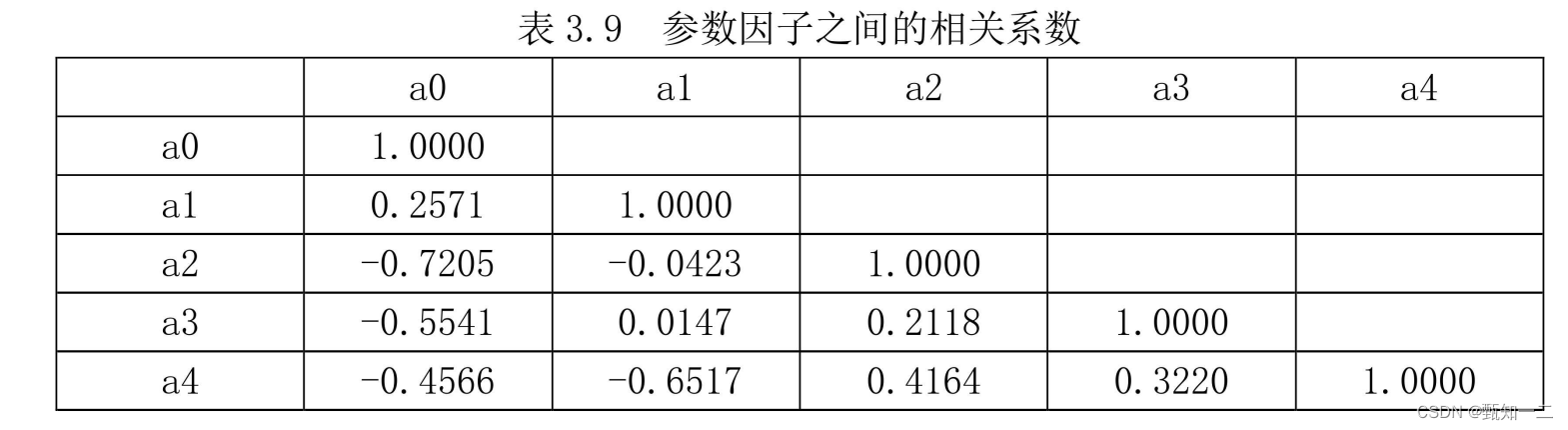
在 VAR 模型中，必须保证模型中的变量都是平稳变量。如果型中的变量都是平稳变量，那么就不用通过多余的检验就可以直接建立VAR模型。如果时间序列不是平稳的，那么就要进行差分或取对数的形式，得到平稳序列再建立VAR模型。
确定 VAR 模型的最优的滞后阶数。比起AIC和BIC信息准则，HQIC信息准则更适用于研究季度和月度数据，由于本文选用的是日度数据，因此我们排除HQIC。训练模型时，增加参数数量会导致模型复杂度的增加，为了防止出现过拟合现象，AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。一般使用BIC选出来的模型比较小，相对来说更稳健，因此根据BIC信息法则最终将VAR模型的滞后阶数确定为1。

三、基于预测IVS的期权估值

根据预测的波动率曲面的6个参数，得出预测的隐含波动率IV；再代入BS定价公式，得出预测的期权估值
model_price(df, date, object, result_df)
:param df: 原始数据
:param date: 模型价格估值的开始时间
:param object: 模型价格的标的
:return: date日的object的模型价格（估值），以及与前一日期权价格的差值（交易信号）
返回result.csv

论文中使用的Vega策略。把在文中拟合的隐含波动率动态曲面和与真实世界中的隐含波动率曲面做比较，当隐含波动率曲面出现明显套利机会时，低买高卖，保持开仓时的delta中性，然后收敛后进行平仓操作
开仓条件：当发现**某期权的隐含波动率被高估数值-某期权的隐含波动率被低估数值>4%**时进行开仓操作。
平仓条件: 买卖期权的隐含波动率被高估数值-被低估数值<3%时，或两者中的剩余期限低于8个交易日时进行平仓操作。
止损: 由于我们在开仓时保持 delta中性，因此几乎不受标的方向的影响，且当我们在剩余期限不低于8天时就进行平仓，因此 gamma 的影响也可以相对忽略不计，所以不设置止损条件
滑点:计算在手续费中，适当提高手续费，手续费为买入开仓与平仓为5元每张，其中包括了佣金，经手费，结算费，卖出开仓与平仓不收取手续费。
资金: 总资金为1000万，为了检验样本外套利策略回测结果的稳定性，我们将其分为5个资金通道(每个通道200万)，每天选取其中一个资金通道建仓最多可以同时抓住5个低买高卖的机会，也就意味着我们最多可以同时买卖10种期权，大大降低了因单一通过某两种期权套利造成的某次大量收益，尽可能杜绝偶然性，以此来体现回测结果的稳定。当5条资金通道全都占用且没有达到平仓条件时则一直持有，如若达到平仓条件，则释放该通道的资金，等待下一次机会。资金占用为保证金+买入期权价-卖出期权价+手续费，做到精确计算手数。
合约选取:由于开平仓条件选取的是期权波动率高估与低估之差，因此我们只选用轻度实值、轻度虚值以及虚值三种类型的期权(即在值程度介于0.95至1.1之间的看涨期权以及在值程度介于0.9至1.05之间的看跌期权)，首先剔除深度实值与深度虚值期权合约，因为模型拟合本就不是完美契合，而离平值的在值程度越远的期权隐含波动率偏差越大，另外尽管初始设定了delta 中性，但delta 也是时变的，因此我们需要尽量保证方向性对收益的影响不大，因此剔除实值期权合约。

四、回测文件生成

期权预估价格，跟前一个交易日的收盘价作对比；做多前20个价格预测上涨的，做空后20个价格预测下跌的
权重根据预测的希腊字母delta加权

买入看涨前20，买看跌后20。对冲delta。利用vega的暴露赚钱

Backtest(df, date_list, object_list, result_df)生成符合规则的回测文件

对冲

在执行策略的过程中我们选择以较低的频率进行对冲，选取了市场流动性较好的时点，包括上午 9:30。
为了防止过度对冲，我们可以设定 Delta 对冲的阈值，仅当需要对冲的 ETF 数量超过已持仓 ETF 数量的一定比例时进行对冲操作。

止盈止损

止盈平仓。如果盈亏比率超过某一阈值（例如设定为 2%），则对组合进行止盈平仓
止损平仓。如果盈亏比率低于某个阈值（例如设定为-2%），则对组合进行止损平仓操作

顺序

先在config里面调整需要处理的品种，然后运行IVS.py，得到IVS_raw_data.pkl，然后再运行predict_AR.py 就可以了

附iv计算的两种实现思路

国内商品期权如黄金、原油为美式期权，可到期日前或到期日行权。用二叉树模型计算
股指期权和ETF期权为欧式期权，仅到期日可行权。用BS公式计算

BS模型的主要函数

calculate_d1_bs():计算D1值,根据公式:
D1 = (ln(S/K) + (r + σ^2/2)T) / (σ√T)
calculate_price_bs():计算期权价格,根据公式:对于看涨期权:
C = SN(d1) - Ke^(-rT)N(d2)
对于看跌期权:P = Ke^(-rT)N(-d2) - SN(-d1)
calculate_delta_bs():计算Δgreeks,根据公式:
Δ = N(d1)
calculate_gamma_bs():计算γgreeks,根据公式:
γ = φ(d1)/(Sσ√T)
calculate_theta_bs():计算θgreeks,根据公式:
θ = -Sφ(d1)σ/(2√T) - rKe^(-rT)N(d2)
calculate_vega_bs():计算vegagreeks,根据公式:
Vega = Sφ(d1)√T
calculate_impv_bs():使用牛顿迭代法计算期权隐含波动率,根据期权价格公式重复计算期权价格,并根据价格误差更新波动率参数,直到收敛得到隐含波动率。

二叉树模型主要函数

generate_tree():生成二叉树,根据波动率v、时间步长dt等参数计算基础资产价格树和期权价格树。
calculate_price_tree():根据生成的期权价格树,读取树根节点的期权价格,即为期权定价结果。
calculate_delta_tree():根据价格树相邻节点价格差异,计算delta对基础资产价格的一阶导数近似。
calculate_gamma_tree():根据delta在两个节点间的差异率,计算gamma对价格的二阶导数近似。
calculate_theta_tree():根据相邻时间步的期权价格差异,计算theta对时间的一阶导数近似。
calculate_vega_tree():比较两个波动率参数生成的期权价格,计算vega对波动率参数的一阶导数。
calculate_greeks_tree():调用上述函数同时计算价格和各希腊字母。
calculate_impv_tree():使用牛顿迭代法,根据期权真实价格反推隐含波动率。

主要根据二叉树模型在时间和价格维度上近似微分,**通过价格树节点间差异来计算期权对各参数的敏感性,即各希腊字母值。**隐含波动率通过迭代逼近期权定价模型。算法思路清晰,实现了期权定价和风险量化的核心功能。

其中生成二叉树的主要公式和原理如下:

计算时间步长dt和时间节点数n,dt=T/n
计算上下波动参数u,d,根据波动率v和时间步长dt,使用估值期公式u=exp(v*sqrt(dt)),d=1/u
计算中性风险概率p,根据无风险收益率a,上下波动参数u,d,使用(a-d)/(u-d)公式计算p
计算基础资产价格树,根节点值为f,随后每层节点根据上下波动u,d乘以上一层对应节点的值
计算期权价格树,叶子层期权价为max(S-K,0),逆向迭代计算内层节点期权价

根据无风险收益率计算折现因子discount

根据中性概率p,p1,p2计算内层节点期权价为上一层对应的节点期权价的加权和

加入早行权条件,期权价取max(迭代值, S-K, 0)
返回基础资产价格树和期权价格树