蓝桥杯2023年第十四届省赛真题-公因数匹配

给定 n 个正整数 Ai，请找出两个数 i, j 使得 i < j 且 Ai 和 Aj 存在大于 1 的公因数。
如果存在多组 i, j，请输出 i 最小的那组。如果仍然存在多组 i, j，请输出 i 最小的所有方案中 j 最小的那组。
笔记：
分解质因数、分解因数（需要学习⭐⭐）
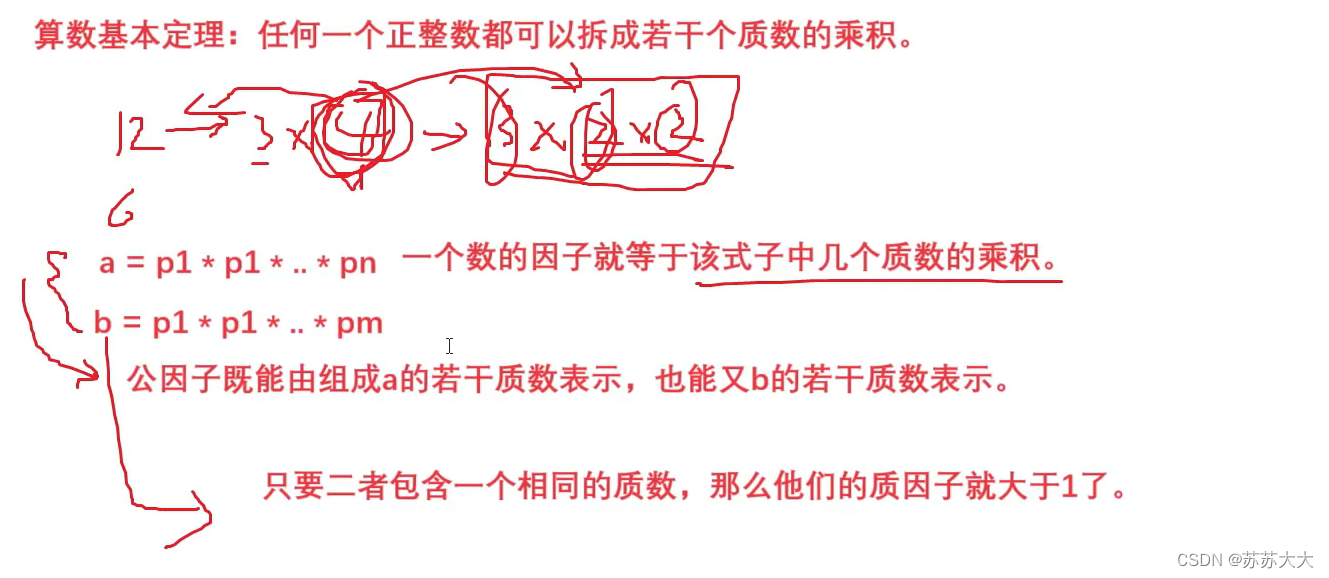
算数基本定理:任何一个正整数都可以拆成若干个质数的乘积。

#include <iostream>
#include<bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f
using namespace std;
//st[i]表示包含质因子i的数字组成的数组
//st[i]={1,2};map<int, vector<int>>st;
int cnt=0;void prim(int x,int pos)
{for(int i=2;i<=x/i;i++){if(x%i)//不等于0说明不是它的一个因子continue;st[i].push_back(pos);while(x%i==0){//把这个因子都除掉后再看下一个因子x/=i;}}if(x>1){st[x].push_back(pos);}return ;
}void solve()
{int n;cin>>n;for(int i=1;i<=n;i++){int x;cin>>x;prim(x,i);//分解质因子}pair<int,int>ans={INF,INF};for(auto[x,y]:st){if(y.size()<2){continue;}if(y[0]<ans.first){ans={y[0],y[1]};}else if (y[0]==ans.first){if(y[1]<ans.second){ans={y[0],y[1]};}}}cout<<ans.first<<" "<<ans.second<<endl;
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t=1;//cin>>t;while(t--)solve();
}