题解:

前序遍历性质： 节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。

中序遍历性质： 节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。

通过以上三步，可确定 三个节点 ：1.树的根节点、2.左子树根节点、3.右子树根节点。

之后进行递归运算

class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {this->preorder = preorder;for(int i = 0; i < inorder.size(); i++)dic[inorder[i]] = i;return recur(0, 0, inorder.size() - 1);}
private:vector<int> preorder;unordered_map<int, int> dic;TreeNode* recur(int root, int left, int right) { if(left > right) return nullptr;                        TreeNode* node = new TreeNode(preorder[root]);          int i = dic[preorder[root]];                            node->left = recur(root + 1, left, i - 1);              node->right = recur(root + i - left + 1, i + 1, right); return node;                                            }
};

 题解:

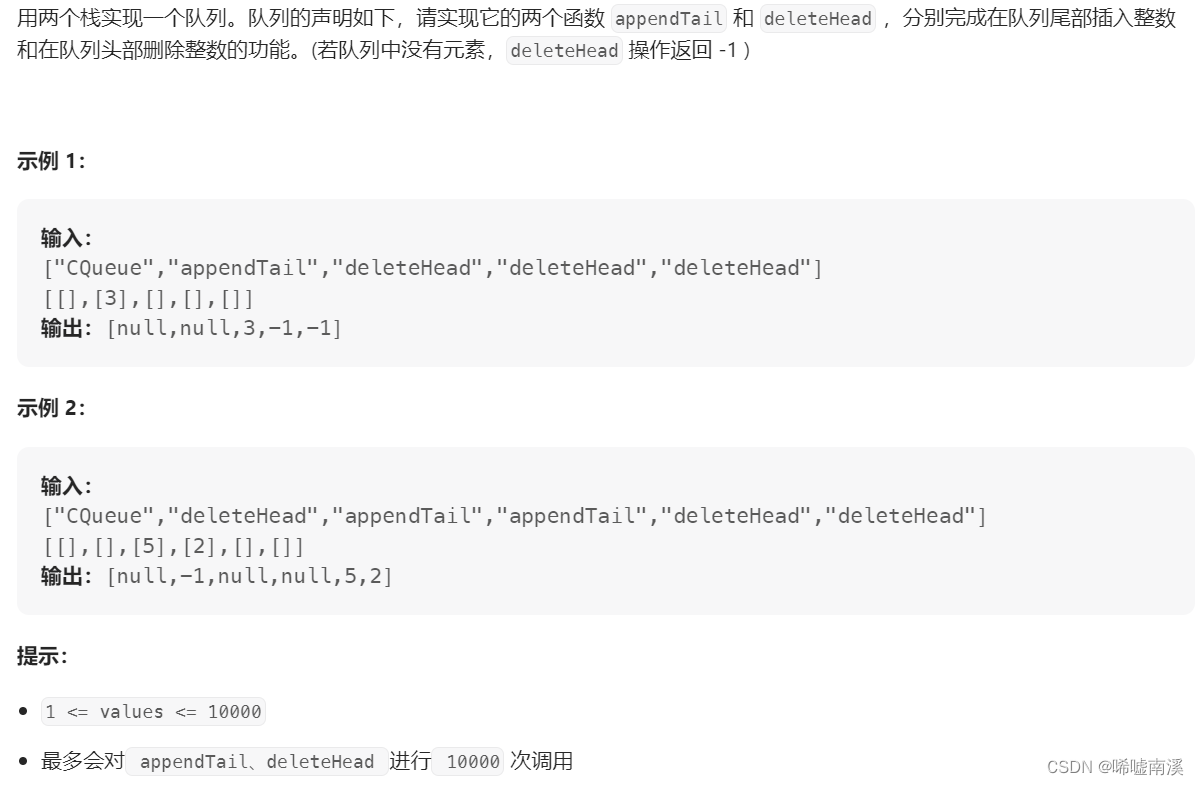
只使用一个栈 stack1 当作队列，另一个栈 stack2 用来辅助操作。

要想将新加入的元素出现栈底，需要先将 stack1 的元素转移到 stack2，将元素入栈 stack1，最后将 stack2 的元素全部回到 stack1。

class CQueue {
public:stack<int> stack1;stack<int> stack2;CQueue() {}void appendTail(int value) {stack1.push(value);}int deleteHead() {if (stack1.empty()) return -1;while (!stack1.empty()){ // 1 -> 2int tmp = stack1.top();stack1.pop();stack2.push(tmp);}// delete headint res = stack2.top();stack2.pop();while (!stack2.empty()){ // 1 <- 2int temp = stack2.top();stack2.pop();stack1.push(temp);}return res;}
};