常用算法——双指针算法

  双指针算法介绍：

    所谓的双指针算法看似十分的神秘，但是实质上就是两个标志查找元素的变量。双指针既可以是我们平常最常说的指针（类似int *类型的数据），也可以是数组的下标。因为对于一个数组数据的查找，通过下标我们照样可以找到相应的数据。

    而我们最经常说到的算法当中的指针并不是平常所说的指针，而是类似于数组下标之类的，方便于查找对应的数据的值。

    而双指针算法就是通过两个“指针”方便我们查找对应的数据以达到对应要求的算法。

  双指针的类型：

  最常见的双指针算法包括两种：一种是碰撞指针的类型，另一种是快慢指针类型。

  碰撞指针：

  碰撞指针指的是两个指针，一个从最左边开始查找元素，另一个从最右边查找元素，最后两个指针相遇的时候就跳出循环。我们将这种从两边开始最终相遇的指针叫做碰撞指针。

  快慢指针：

    快慢指针指的是两个从同一位置开始的指针。但是我们这两个指针移动的速度不同。我们可以根据题目要求进行判断。例如设置一个慢指针一次移动一步，设置一个快指针一次移动两步。

    通常情况下快慢指针用于带有循环节点的情况，例如：对于我们循环链表数据的查找就使用了快慢指针。但是不仅仅是循环链表，只要我们根据题目当中的要求进行分析，存在循环的情况就可以尝试使用快慢指针进行问题的解决。

题目示例：

 题目一： 查找总价格为目标值的两个商品

 

  解题思路：  

   思路一：暴力查找：

  这道题想要解决很简单。最简单的解决的方法就是暴力查找。我们只需要将数据两两匹配，直到查找到符合要求的目标返回即可。但是我们暴力匹配的时间复杂度很高。该算法是一个O(N^2)的算法。 很多时候都无法通过，所以我们就需要想到对代码进行优化。

  运行代码：
#include<iostream>
#include<vector>
using namespace std;vector<int> twoSum(vector<int>& price, int target)
{//暴力查找算法解决问题vector<int> ret;for (int i = 0; i < price.size()-1; i++){for (int j = i+1; j < price.size(); j++){if (price[i] + price[j] == target){ret.push_back(price[i]);ret.push_back(price[j]);return ret;}}}return ret;
}int main()
{vector<int> ret={ 3, 9, 12, 15 };int target = 18;vector<int> tmp=twoSum(ret, target);for (auto e : tmp){cout << e << " ";}return 0;
}
    运行结果：

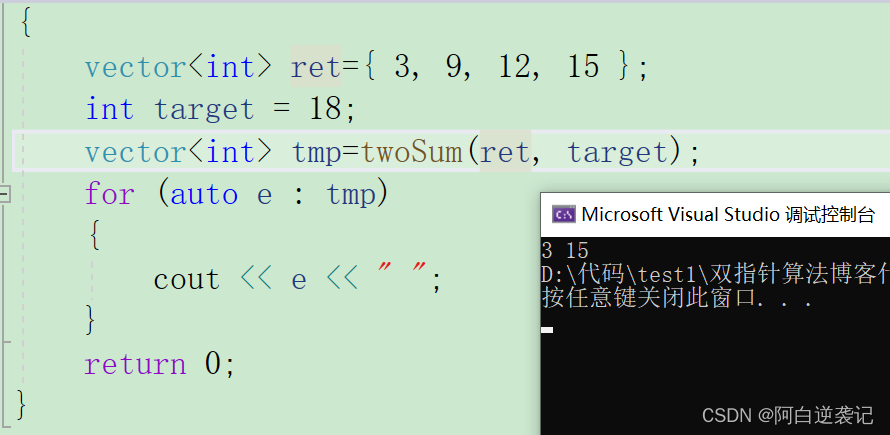
  我们会发现VS当中运行一切正常，但是放到力扣上面就无法通过：

  显示超出时间限制，这个时候我们就应该想到优化代码。

  思路二：双指针算法

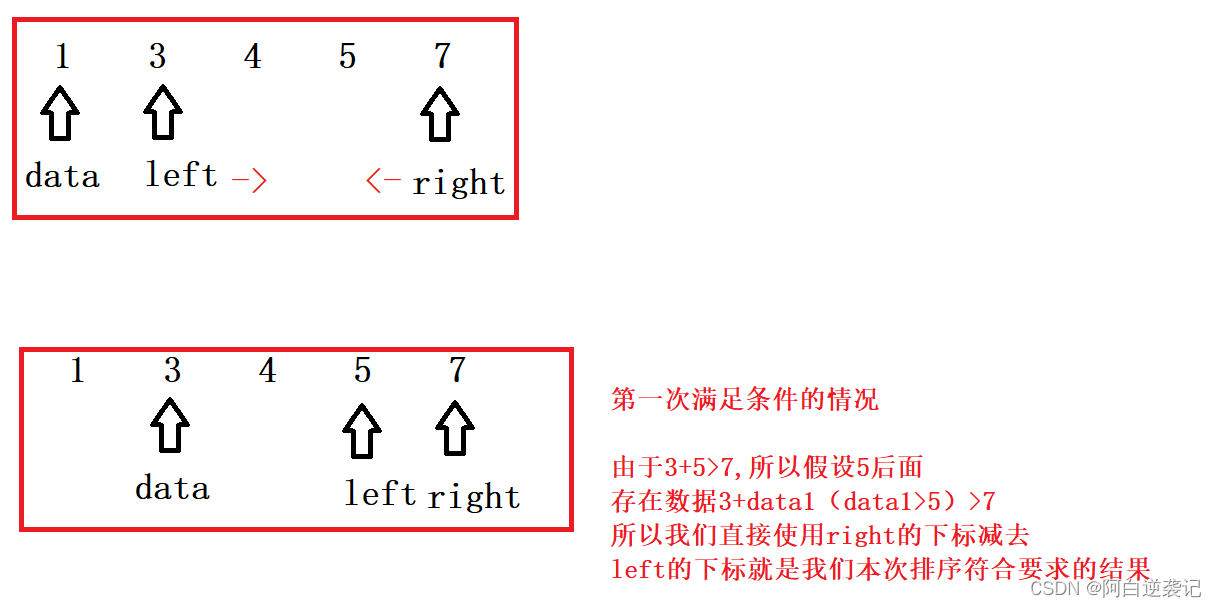
  我们仔细阅读题目要求会发现有一个很神奇的条件：数据当中的数据为升序，所以我们这个时候就可以使用双指针算法进行代码的优化。

  我们可以使用碰撞指针，设置两个从不同端开始的指针。从最左端找到一个数据，从最右端找到一个数据。

    将这两个数据相加，如果得到的结果大于想要查找的目标的值，就将右边的指针向左进行移动。如果得到的结果小于想要查找的目标的值，就将左边的指针向右进行移动。如果符合条件的值存在的话就一定可以查到。

  算法原理解析：

  为什么我们使用碰撞指针如果目标数据存在就一定可以查找到我们想要的数据呢？

  假如存在符合条件的数据因为它是固定的，那么它对应的另一个答案也是固定的。无非就三种情况：我们找到的符合条件的数据是两个数据当中较小的那一个，我们找到的数据是两个当中较大的那一个，我们找到的数据相等。

  无论是这两种的哪一种，只要我们都可以通过目标值进行推算出来另外一个值，另外一个值也无非是大于等于小于这三种情况。又因为我们的数组是有序的，假设我们先固定的是较大的值，另外一个值还没有找到，相加之和一定比目标值小，left一定需要向右进行移动。如果我们先固定的是较小的值，较大的值没有找到，相加之和就一定比目标值大。所以我们需要将right向左进行移动。

    代码编写：

下面我们就来使用碰撞指针算法进行解决该问题：

#include<iostream>
#include<vector>
using namespace std;vector<int> twoSum(vector<int>& price, int target)
{//暴力查找算法解决问题vector<int> ret;int left = 0, right = price.size()-1;while (left < right){if (price[left] + price[right] < target){left++;}else if (price[left] + price[right] > target){right--;}else{ret.push_back(price[left]);ret.push_back(price[right]);return ret;}}return ret;
}int main()
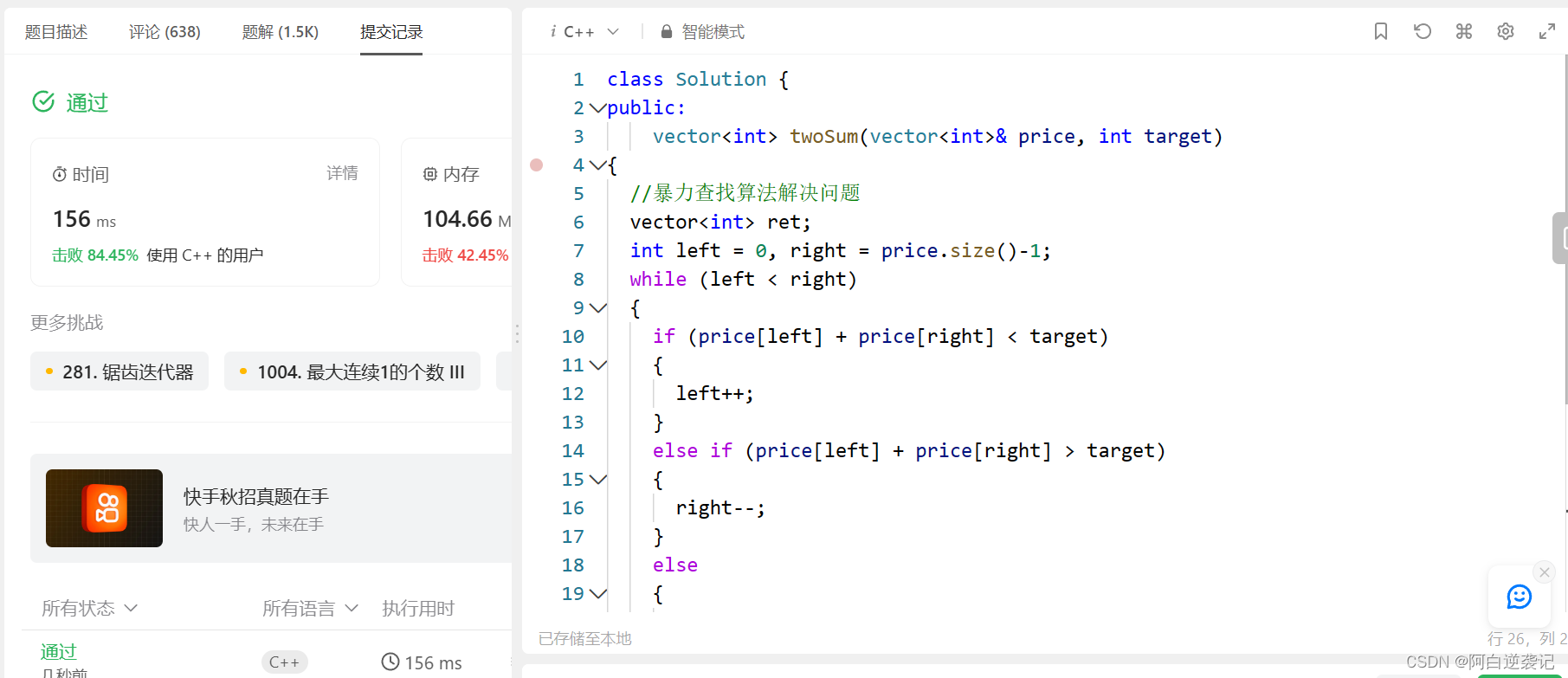
{vector<int> ret = { 3, 9, 12, 15 };int target = 18;vector<int> tmp = twoSum(ret, target);for (auto e : tmp){cout << e << " ";}return 0;
}
   运行结果:

  题目示例二：快乐数

  

    解题思路：

    思路一：暴力计算：

  这道题的解题方法暴力计算其实和双指针算法的差别不大，但是使用双指针算法可能会更加省心一些。我们依次来实现这两种算法。

  对于一个数据判断是不是快乐数，我们只需要重复一个操作：取个位数求平方相加即可。最后的循环结果等于1，就代表是快乐数。不为1那么就不是快乐数。其中需要我们特别注意的是不是快乐数的判断：我们需要创建一个vector对象，统计每一次产生的结果，如果vector对象当中原本存在的数据再次出现，且该值不等于1就代表我们的循环结束，该数不为快乐数。

  代码示例：
#include<iostream>
#include<vector>
using namespace std;int operatChange(int n)
{int tmp = 0;int sum = 0;while (n){tmp = n %10;sum = sum + tmp * tmp;n /= 10;}return sum;
}bool in_ret(vector<int> ret, int data)
{for (auto e : ret){if (data == e){return true;}}return false;
}bool isHappy(int n) 
{vector<int> ret;n = operatChange(n);while (!in_ret(ret,n)){ret.push_back(n);n = operatChange(n);}if (n == 1){return true;}else{return false;}
}int main()
{int data = 19;if (isHappy(data)){cout << data << "是快乐数" << endl;}else{cout << data << "不是快乐数" << endl;}return 0;
}
  运行结果：

  思路二：快慢指针

  这道题使用双指针进行求解其实和我们正常的暴力求解差不多，并没有起到太大的优化作用。在这里使用快慢指针仅仅是为了加深我们对双指针算法的学习。下面我们使用快慢指针算法进行求解：

  我们可以设置两个指针，一个快指针，一个慢指针。快指针每一次向前走两步，慢指针每一次向前走一步。如果存在循环节点那么这两个指针就一定可以相遇。所以我们就可以将相遇的数据的值作为判断条件。

  代码示例：

  

#include<iostream>
#include<vector>
using namespace std;int operatChange(int n)
{int tmp = 0;int sum = 0;while (n){tmp = n % 10;sum = sum + tmp * tmp;n /= 10;}return sum;
}bool isHappy(int n)
{//使用双指针算法判断是否是快乐数int fast = -1;int slow = 0;fast = operatChange(n);slow =n;while (fast!=slow){fast=operatChange(fast);fast = operatChange(fast);slow = operatChange(slow);}if (fast == 1){return true;}else{return false;}
}int main()
{int data = 19;if (isHappy(data)){cout << data << "是快乐数" << endl;}else{cout << data << "不是快乐数" << endl;}return 0;
}
   运行结果：

  原理证明：

  之前我们说到：快慢指针最适合的应用场景是存在循环节点的时候。我们只需要证明可以该题目当中无论什么情况都可以落入循环当中即可。

  首先我们有两种情况，一种是是快乐数的情况，一种是不是快乐数的情况。如果是快乐数的时候我们最后的数据会变成1，之后无论进行多少次操作都是1，构成循环。另一种不是快乐数的情况：我们可以列举一个不是快乐数的示例:2->4->16->37->58->89->145->42->20->4

  当不是快乐数的数据在经过操作之后我们的数据会再次得到列表当中出现过的数据，这个时候就进入了一个循环。所以我们本道题目当中无论是什么情况最终都会进入循环当中，这个时候就可以通过判断相遇的值是否为1，进而判断是否为快乐数。

  题目示例三：移动零

    

解题思路：

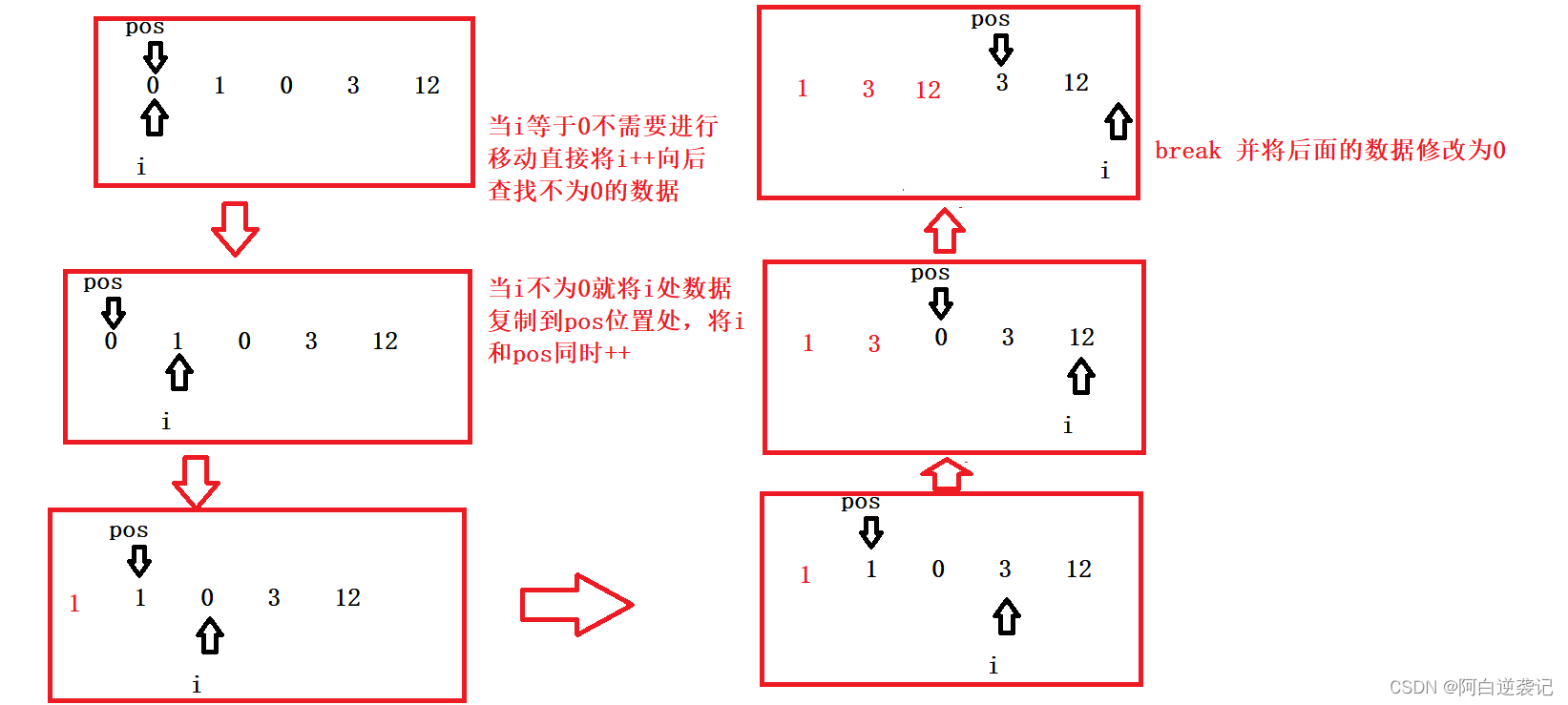
  这道题就是一个很简单的双指针的问题。我们可以从前向后进行查找，找到不为0的数据就将它移动到前面。我们可以设置两个指针进行控制这个操作：一个指针用于查找非零的元素，一个指针用于保存查找到非零元素需要移动到的位置。

  代码示例：

#include<iostream>
#include<vector> 
using namespace std;void moveZeroes(vector<int>& nums)
{//直接从前向后进行查找，找到非0的元素就将其向前移动最终得到想要的结果int pos=0;for(int i=0;i<nums.size();i++){if(nums[i]!=0){//不等于0就将数据向前移动nums[pos]=nums[i];pos++; }} //当循环结束之后，将pos之后的数据全部置为0while(pos<nums.size()) {nums[pos]=0;pos++;}return;
}int main()
{vector<int> ret;ret.push_back(0);ret.push_back(1);ret.push_back(0);ret.push_back(3);ret.push_back(12);moveZeroes(ret);for(int i=0;i<ret.size();i++){cout<<ret[i]<<" ";}return 0;
}

  运行结果：

  题目示例四：两数之和

  

解题思路：

  这道题和我们之前写的查找价格为目标值的两件商品可以说是一模一样。但是我们题目当中没有具体说明数组数据有序，所以我们就需要先将数组进行排序之后再查找为目标值的两个数据即可。

代码示例：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;vector<int> twoSum(vector<int>& nums, int target) 
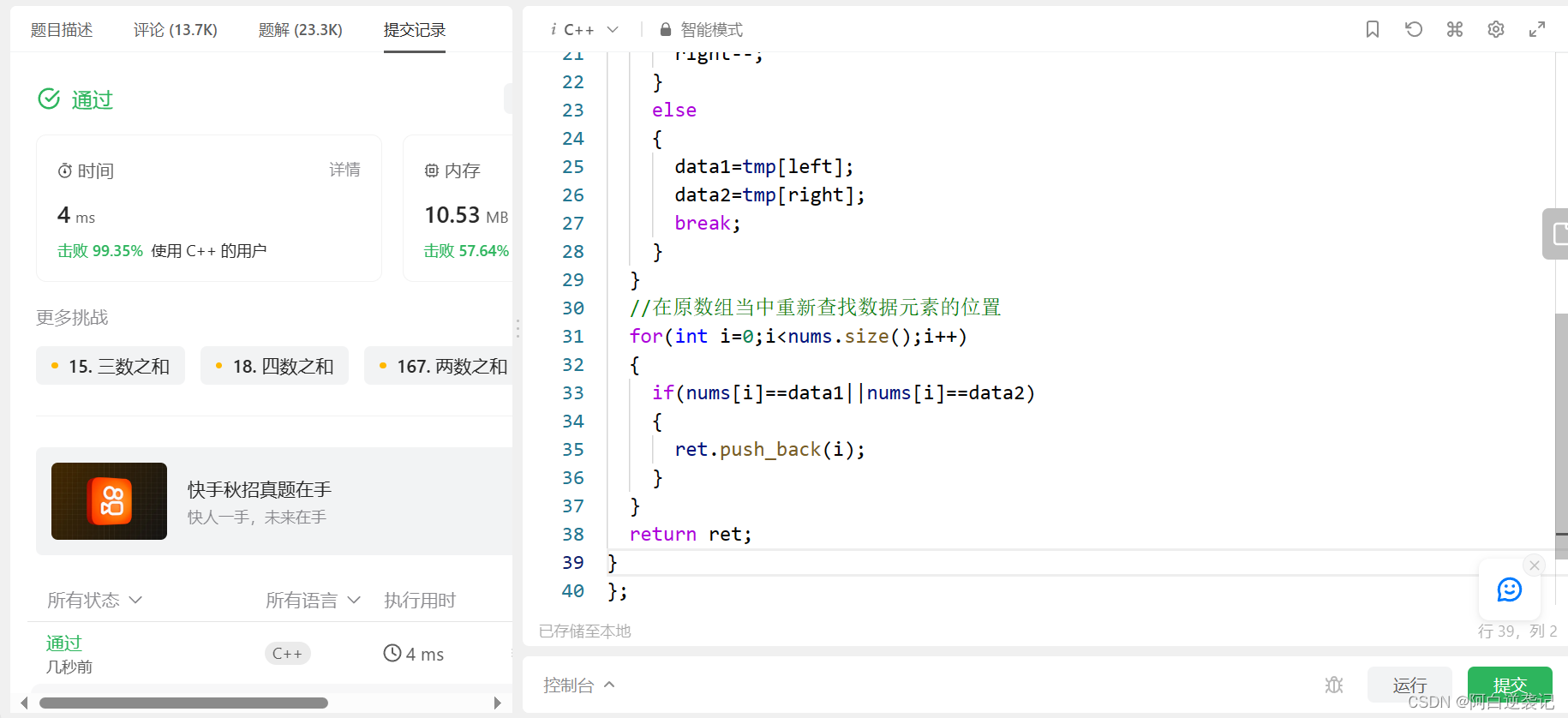
{//首先对数组当中的数据进行排序vector<int> tmp=nums;vector<int> ret;sort(tmp.begin(),tmp.end());int left=0;int right=nums.size()-1;int data1=0;int data2=0;while(left<right){if(tmp[left]+tmp[right]<target){left++;}else if(tmp[left]+tmp[right]>target){right--;}else{data1=tmp[left];data2=tmp[right];break;}}//在原数组当中重新查找数据元素的位置for(int i=0;i<nums.size();i++){if(nums[i]==data1||nums[i]==data2){ret.push_back(i);}}return ret; 
}int main()
{vector<int> ret;ret.push_back(2);ret.push_back(7);ret.push_back(11);ret.push_back(15);int target=9;vector<int> out=twoSum(ret,target);for(int i=0;i<out.size();i++){cout<<out[i]<<" ";}return 0;
}

运行结果：

  题目示例五：有效三角形的个数

    

  解题思路：

        思路一：暴力计算

       当我们的问题较为复杂的时候我们就重新一步一步进行对代码进行优化，所以我们先编写一个可以运行通过的代码，方便我们对题目的理解。

     当我们看到题目的时候，最开始的思路肯定是暴力匹配的算法，使用三个循环嵌套，每一次选出三个数据，判断这三个数据是否可以组成一个三角形。判断是否可以组成三角形的条件为：两边之和大于第三边，两边之差小于第三边。我们可以将这个条件转化为最短的两条边相加大于最长的边。我们可以通过思考得到该三边可以组成三角形。（证明省略）所以我们要想快速找到最短的两条边，就需要保证数组有序，位于前面的两个数据一定是较小的两个数据。所以我们可以写出如下的代码。

    代码示例：
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int triangleNumber(vector<int>& nums) 
{int count=0; sort(nums.begin(),nums.end());for(int i=0;i<nums.size()-2;i++){for(int j=i+1;j<nums.size()-1;j++){for(int k=j+1;k<nums.size();k++){//判断是否可以组成三角形，如果可以组成三角形就进行统计 if(nums[i]+nums[j]>nums[k]){count++;}}}}return count;
}int main()
{vector<int> ret;ret.push_back(4);ret.push_back(2);ret.push_back(3);ret.push_back(4);cout<<triangleNumber(ret);return 0;
}
    运行结果：

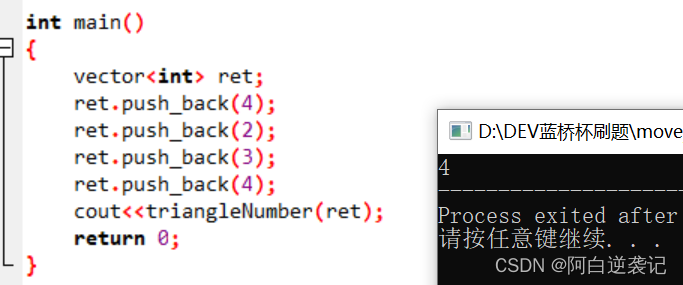
   但是毫无疑问的是，我们的程序肯定会超出时间限制。毕竟我们的算法是一个O（N^3）的算法。所以我们需要对上述代码进行优化。

   思路二：多指针优化

  这个时候就需要使用到我们今天所学到的内容了：我们可以使用指针对我们的代码进行优化。

  我们可以设计三个指针，由于之前我们将数组已经排好序了。所以我们只要固定一个数据，那么使用另外两个数据就可以将问题转化为求两个数据之和的问题。

  我们将固定好的数据以及之前的数据排除，之后的数据进行判断，设置一个left指针，设置一个right指针。我们可以将原本O（N^2）的算法转换成为O（N）的算法，使用一趟排序判断出需要移动的次数。

  由于我们需要求得是较小的两个数相加大于较大的两个数。所以我们只需要求满足条件的最小的第二个数据即可。因为我们的数组是有序的，所以我们前面的数据满足条件，后面指针之间的数据一定也满足条件。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/617387.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

halcon-轴断面检测定位

halcon-轴断面检测定位

前言 通常情况下轴检测时&#xff0c;通常会检测轴的各个阶段的长度。但是由于各种原因&#xff0c;在轴断面的区域现实不明显&#xff0c;无法正确提取&#xff0c;这时候需要根据轴断面的突出部分进行检测&#xff0c;但是由于部分轴的粗轴和细轴区域的宽度差距相当接近&…
阅读更多...
安卓数据怎么恢复？十大顶级Android数据恢复软件

安卓数据怎么恢复？十大顶级Android数据恢复软件

Android 是移动设备的顶级操作系统。由于许多不确定的情况&#xff0c;会发生数据丢失。数据恢复软件有助于挽救丢失的数据。在这里&#xff0c;让我们讨论一下 前 10 名最佳 android 数据恢复软件。 十大顶级Android数据恢复软件 1.奇客数据恢复 奇客数据恢复是由奇客软件软件…
阅读更多...
Blender4.0 下载地址及安装教程

Blender4.0 下载地址及安装教程

Blender是一款开源的3D计算机图形软件&#xff0c;广泛应用于动画制作、游戏开发、建模、渲染等领域。它提供了一套强大的工具和功能&#xff0c;让用户能够进行三维建模、动画制作和视觉效果的创作。 Blender支持多种文件格式的导入和导出&#xff0c;使用户能够与其他软件进…
阅读更多...
浮点数的表示

浮点数的表示

王道考研ppt总结&#xff1a; 二、个人理解 浮点数解决的是定点数的位数局限&#xff0c;导致表示范围有限的问题 阶码&#xff1a;由阶符和数值部分组成&#xff0c;阶符为&#xff0c;小数点向左移动&#xff0c;否则向右移动&#xff1b;数值部分&#xff0c;是底数的几次幂…
阅读更多...
【CSS】一篇文章讲清楚screen、window和html元素的位置：top、left、width、height

【CSS】一篇文章讲清楚screen、window和html元素的位置：top、left、width、height

一个Web网页从内到外的顺序是&#xff1a; 元素div,ul,table... → 页面body → 浏览器window → 屏幕screen 分类详情屏幕screen srceen.width - 屏幕的宽度 screen.height - 屏幕的高度&#xff08;屏幕未缩放时&#xff0c;表示屏幕分辨率&#xff09; screen.availLeft …
阅读更多...
Electron 桌面端应用的使用 ---前端开发

Electron 桌面端应用的使用 ---前端开发

Electron是什么&#xff1f; Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个 JavaScript 代码代码库并创建 在Windows上运行的跨平台应用 macOS和Linux——不需要本地开发 经验。 入门…
阅读更多...
Spring Boot - 利用MDC（Mapped Diagnostic Context）实现轻量级同步/异步日志追踪

Spring Boot - 利用MDC（Mapped Diagnostic Context）实现轻量级同步/异步日志追踪

文章目录 Pre什么是MDC&#xff08;Mapped Diagnostic Context&#xff09;Slf4j 和 MDC基础工程工程结构POMlogback-spring.xmlapplication.yml同步方式方式一&#xff1a; 拦截器自定义日志拦截器添加拦截器 方式二&#xff1a; 自定义注解 AOP自定义注解 TraceLog切面 测试…
阅读更多...
解析器模式：面向对象设计中的表达式评估与语法树构建策略

解析器模式：面向对象设计中的表达式评估与语法树构建策略

解释器模式&#xff08;Interpreter Pattern&#xff09;是一种行为设计模式&#xff0c;它定义了一种语言&#xff0c;并使用该语言来解释句子。这种模式用于描述如何构成一个简单的语言解析器。在Java中实现解释器模式通常涉及一个抽象表达式接口、具体表达式类&#xff08;终…
阅读更多...
HCIP课后习题之一

HCIP课后习题之一

1、路由协议用工作机制上分为那几种&#xff1f;分别是&#xff1f; A&#xff1a;两种。分别是静态路由和动态路由&#xff08;可分为IGP和EGP&#xff09; 2、IGP和EGP协议有哪些&#xff1f; A&#xff1a;IGP: RIP、OSPF、ISIS、EIGRP EGP: BGP 3、路由优先级的用途&…
阅读更多...
Leetcode - 周赛392

Leetcode - 周赛392

目录 一&#xff0c;3105. 最长的严格递增或递减子数组 二&#xff0c;3106. 满足距离约束且字典序最小的字符串 三&#xff0c;3107. 使数组中位数等于 K 的最少操作数 四&#xff0c;3108. 带权图里旅途的最小代价 一&#xff0c;3105. 最长的严格递增或递减子数组 本题求…
阅读更多...
Steam平台游戏发行流程

Steam平台游戏发行流程

Steam平台游戏发行流程 大家好我是艾西&#xff0c;一个做服务器租用的网络架构师也是游戏热爱者&#xff0c;经常在steam平台玩各种游戏享受快乐生活。去年幻兽帕鲁以及雾锁王国在年底横空出世&#xff0c;幻兽帕鲁更是在短短一星期取得了非常好的成绩&#xff0c;那么作为游戏…
阅读更多...
Python工程师面试高频题：return 和 yield之间到底有啥区别？

Python工程师面试高频题：return 和 yield之间到底有啥区别？

在编程语言 Python 中&#xff0c;yield 和 return 是两个在函数中用于返回值的关键字&#xff0c;但它们在功能和使用场景上有着本质的区别。理解这两者的区别&#xff0c;对于编写更高效、更灵活的 Python 代码至关重要。 看图说话 首先我们来看下面这张图片&#xff0c;该…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023