什么是特征预处理?

通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
1包含内容
- 数值型数据的无量纲化:
- 归一化
- 标准化
2特征预处理API
sklearn. preprocessing
为什么要进行归一化 or 标准化?
特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级,容易影响(支配)目标结果,使得一些算法无法学习到其它的特征。
归一化
1定义
通过对原始数据进行变换把数据映射到(默认为[0,1])之间
2公式
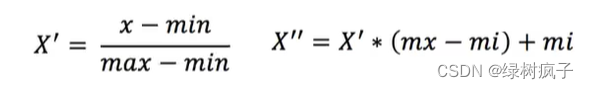
作用于每一列,max为一列的最大值,min为一列的最小值,那么X"为最终结果,mx,mi分别为指定区间值默认mx为1,mi为0
3API
- sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)…)
- MinMaxScalar.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后的形状相同的array
- MinMaxScalar.fit_transform(X)
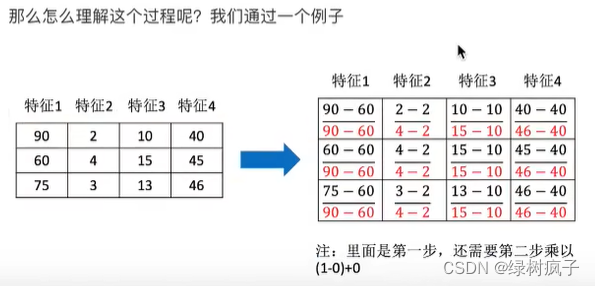
4数据计算
我们对以下数据进行运算:
milage,Liters, consumtime,target
40920,8.326976,0.953952,3
14488,7.153469,1.673904,2
26052,1.441871,0.805124,1
75136,13.147394,0.428964,1
38344,1.669788,0.134296,1
- 分析
- 1、实例化MinMaxScalar
- 2、通过fit_transform转换
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
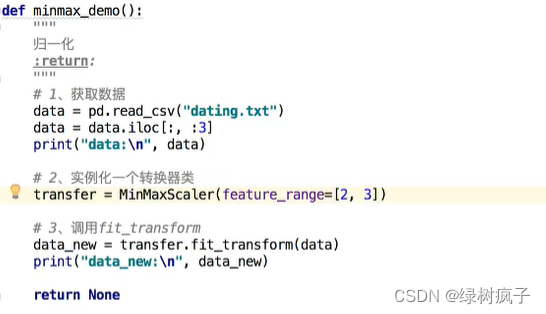
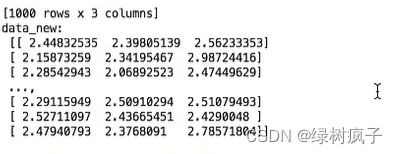
问题:如果数据中异常点较多,会有什么影响?
异常值
5归一化总结
注意最大值最小值是变化的,另外,最大值与最小值非常容易受异常点影响,所以这种方法篆棒性较差,只适合传统精确小数据场景。
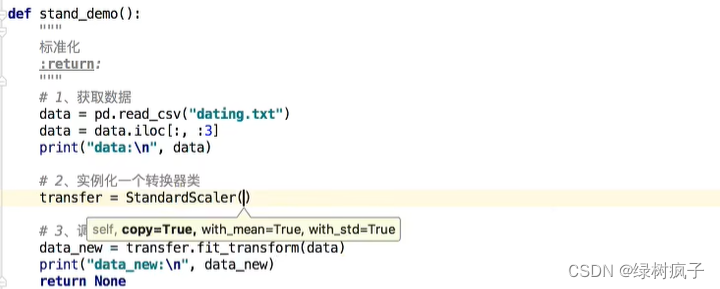
标准化
1定义
通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内
2公式
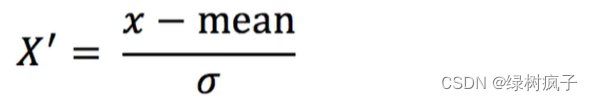
作用于每一列,平均值为mean,标准差为σ
- 对于归一化︰如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
- 对于标准化:如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大,从而方差改变较小。
3API
- sklearn.preprocessing.StandardScaler()
- 处理之后,对每列来说,所有数据都聚集在均值为0附近,标准差为1
- StandardScaler.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后的形状相同的array
4数据计算

5标准化总结
在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景。
降维
降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程。
此处的降维:降低特征的个数,使特征与特征之间不相关
- 降低随机变量的个数
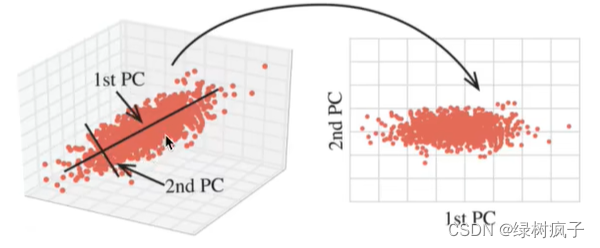
- 相关特征(correlated feature)
- 相对湿度与降雨量之间的相关
- 等等
正是因为在进行训练的时候,使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强,对于算法学习预测会影响较大
降维的两种方式
- 特征选择
- 主成分分析(可以理解一种特征提取的方式)
特征选择
1定义
数据中包含冗余或相关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。
2方法
- Filter(过滤式):主要探究特征本身特点、特征与特征和目标值之间关联
- 方差选择法:低方差特征过滤
- 相关系数:特征与特征之间的相关程度
- Embedded(嵌入式):算法自动选择特征(特征与目标值之间的关联)
- 决策树:信息嫡、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
3模块
sklearn.feature_selection
4过滤式
4.1低方差特征过滤
删除低方差的一些特征,前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。
- 特征方差小:某个特征犬多样本的值比较相近
- 特征方差大:某个特征很多样本的值都有差别
4.1.1API
- sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
- 删除所有低方差特征
- Variance.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
4.1.2数据计算
1、初始化VarianceThreshold,指定阀值方差
2、调用fit_transform
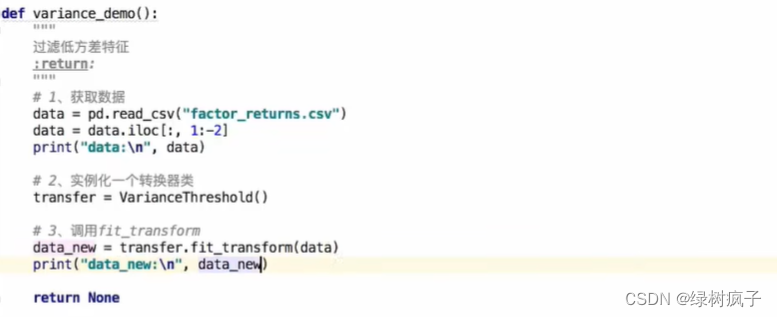
transfer = VarianceThreshold(threshold=10)进行限制阈值,过滤不太重要的特征
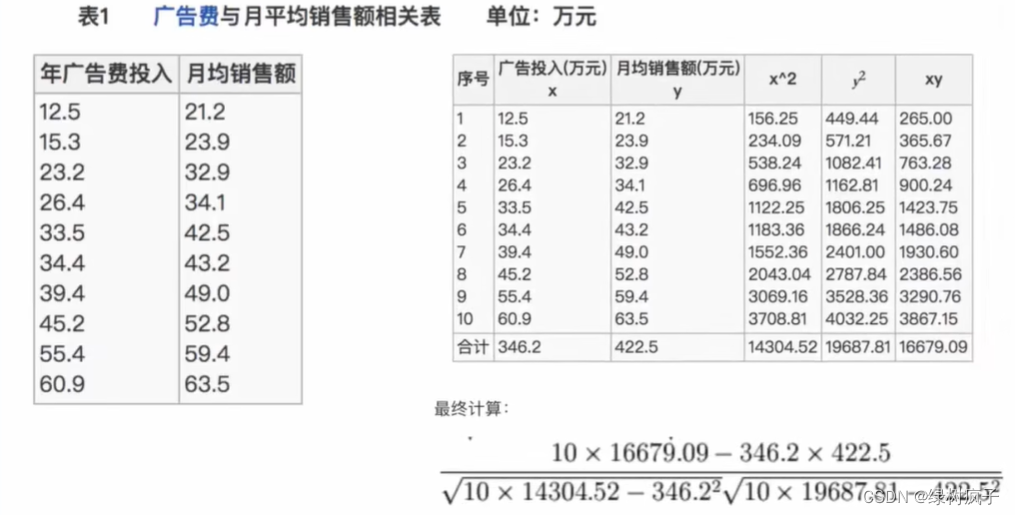
4.2相关系数
- 皮尔逊相关系数(Pearson Correlation Coefficient)
- 反映变量之间相关关系密切程度的统计指标
4.2.1公式
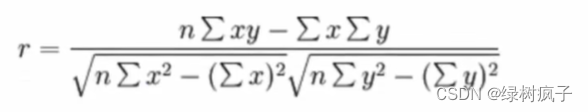
列题
4.2.2特点
相关系数的值介于-1与+1之间,即-1 ≤ r ≤ +1。其性质如下:
- 当 r>0时,表示两变量正相关,r<0时,两变量为负相关
- 当 |r|=1时,表示两变量为完全相关,当 r=0时,表示两变量间无相关关系
- 当 0<|r|<1 时,表示两变量存在一定程度的相关。且 |r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
- 一般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著性相关;0.7≤lrl<1为高度线性相关
4.2.3API
- from scipy.stats import pearsonr
- ×:(N)array_like
- y :(N,)array_like Returns:(Pearson’s correlation coefficient, p-value)
#计算某两个变量之间的相关系数
r =pearsonr(data["pe_ratio"], data["pb_ratio"])
print("相关系数: \n", r)
r2 = pearsonr(data['revenue'], data['total_expense'])
print("revenue与total_expense之间的相关性:\n",r2)
我们也可以通过画图来观察结果
import matplotlib.pyplot as plt
plt.figure(figsize=(20,8),dpi=100)
plt.scatter(data['revenue'], data['total_expense '])
plt.show ( )
若特征与特征之间相关性很高:①选取其中一个②加权求和③主成分分析
主成分分析
- 定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量。
- 作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
- 应用:回归分析或者聚类分析当中。
1例子
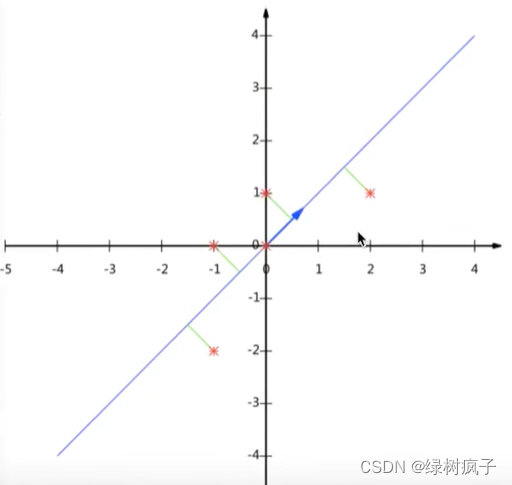
找到一个合适的直线,通过一个矩阵运算得出主成分分析的结果
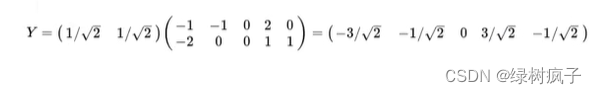
2API
- sklearn.decomposition.PCA(n_components=None)
- 将数据分解为较低维数空间
- n_components:
- 小数:表示保留百分之多少的信息
- 整数:减少到多少特征
- PCA.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后指定维度的array
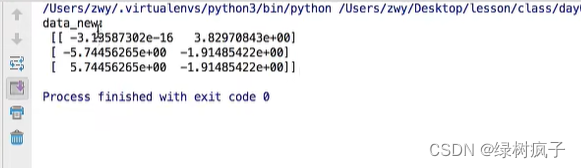
整数:

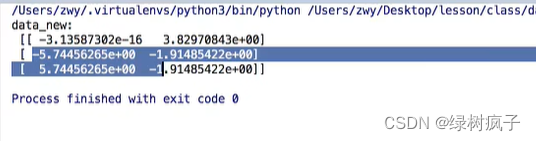
小数:

3案例
探究用户对物品类别的喜好细分
| 用户 | 物品类别 |
|---|---|
| user_id | aisle |
①需要将user_id和aisle放在同一个表中——合并
②找到user_id和aisle——交叉表和透视表
③特征冗余过多——>PCA降维
import pandas as pd
#1、获取数据
order_products=pd.read_csv("./instacart/order_products_prior.csv")
products=pd.read_csv("./instacart/products.csv")
orders=pd.read_csv("./instacart/orders.csv")
aisles=pd.read_csv("./instacart/aisles.csv")#2、合并
tab1=pd.merge(aisles,products,on=["aisle_id","aisle_id"])
Lab2=pd.merge(tab1,order_products,on=["product_id","product_id"])
tab3=pd.merge(tab2,orders,on=["order_id","order_id"])#3、找到user_id和aisle之间的关系
table=pd.crosstab(tab3["user_id"],tab3["aisle"])
data =table[ :10000]#数据过多,取前10000个#4、PCA降维
from sklearn.decomposition import PCA
#1)实例化一个转换器类
transfer=PCA(n_components=0.95)
#2)调用fit_transform
data_new=transfer.fit_transform(data)