Day55 动态规划 part15
392.判断子序列
我的思路:
自己还是只能想到双指针法
解答:
class Solution {public boolean isSubsequence(String s, String t) {if(s.length() == 0) {return true;}if(s.length() > t.length() || t.length() == 0) {return false;}char[] sc = s.toCharArray();char[] tc = t.toCharArray();int s1, t1 = 0;for(s1 = 0, t1 = 0; s1 < sc.length && t1 < tc.length; t1++) {if(tc[t1] == sc[s1]) {s1++;}}if(s1 == sc.length) {return true;}return false;}
}
如果用动态规划的思想解题
状态转移方程:
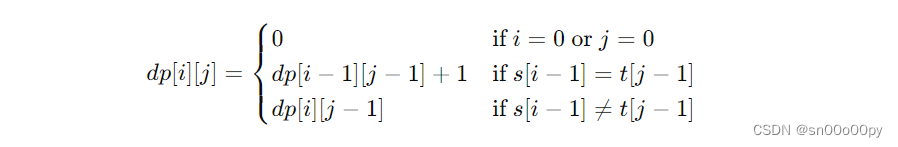
class Solution {public boolean isSubsequence(String s, String t) {int slen = s.length();int tlen = t.length();char[] sc = s.toCharArray();char[] tc = t.toCharArray();int[][] dp = new int[slen + 1][tlen + 1];for(int i = 1; i <= slen; i++) {for(int j = 1; j <= tlen; j++) {if(sc[i - 1] == tc[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = dp[i][j - 1];}}}return dp[slen][tlen] == slen;}
}
115.不同的子序列
我的思路:
跟上一题代码其实差不多,但是现在s是母串,t是待匹配的子串
所以这道题我的dp定义为dp[t.length() + 1][s.length() + 1]
跟上一题状态转移方程几乎差不多

i == j(字符相等时)
dp[i][j] = dp[i - 1][j - 1] + 1 --> 现在不是+1,是 + dp[i][j - 1]
我们可以选择不使用 s 的第 j 个字符来构成子序列,那么这种情况的数量就是 dp[i][j - 1]
我们也可以选择使用 s 的第 j 个字符来构成子序列,那么这种情况的数量就是 dp[i - 1][j - 1]
i != j(字符串不相等时)
dp[i][j] = dp[i ][j - 1]
解答:
class Solution {public int numDistinct(String s, String t) {int[][] dp = new int[t.length() + 1][s.length() + 1];for(int i = 1; i <= t.length(); i++) {dp[i][0] = 0;}for(int j = 0; j <= s.length(); j++) {dp[0][j] = 1;}for(int i = 1; i <= t.length(); i++) {for(int j = 1; j <= s.length(); j++) {if(t.charAt(i - 1) == s.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];}else {dp[i][j] = dp[i][j - 1];}}}return dp[t.length()][s.length()];}
}