探索FSM （有限状态机）应用-编程知识

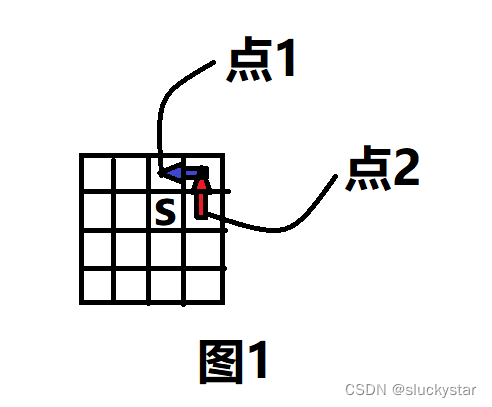
有限状态机（FSM） 是计算机科学中的一种数学模型，可用于表示和控制系统的行为。它由一组状态以及定义在这些状态上的转换函数组成。FSM 被广泛用于计算机程序中的状态机制。

有限状态机（FSM）应用场景

在各种自动化系统的应用： 例如交通信号灯、地铁站的旋转闸门、银行自动取款机等。通过对状态和转换函数的定义，可以实现对系统行为的精确控制。

交通信号灯状态流转图

地铁站的旋转闸门状态流转图

银行自动取款机状态流转图
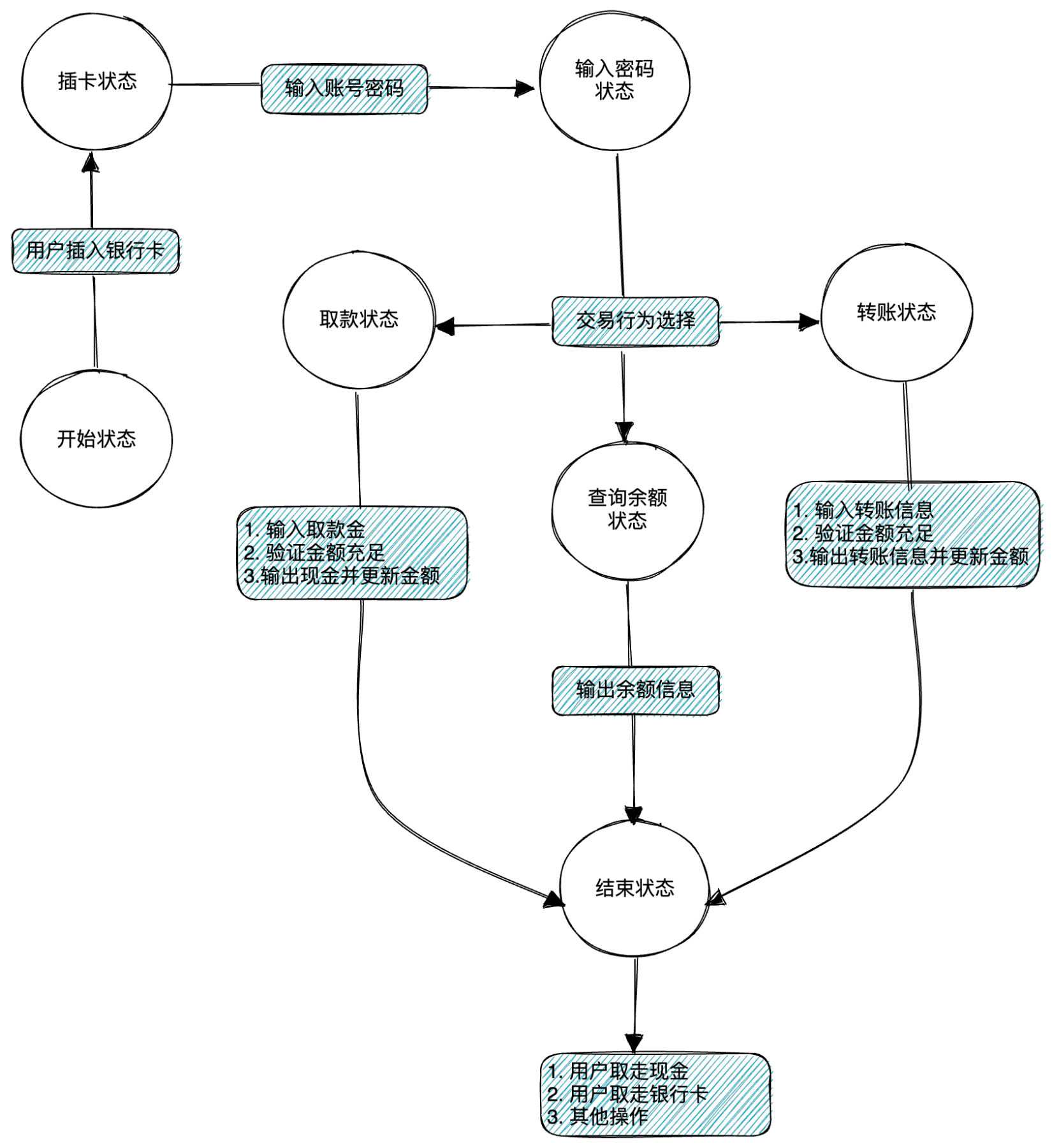
在编程领域的应用： 例如在编写编译器和解释器时，可以使用有限状态机（FSM) 来处理词法分析。例如：JSON.Parse
在Notion中应用： 可以使用 有限状态机（FSM) 的相关概念来构建各种工作流程，例如状态转换图、状态转换表等。
在web中应用： 我们熟悉的 Promise 也是一个状态机，具有三个状态：pending、resolved。rejected。

Promise状态流转图

登录功能流转图

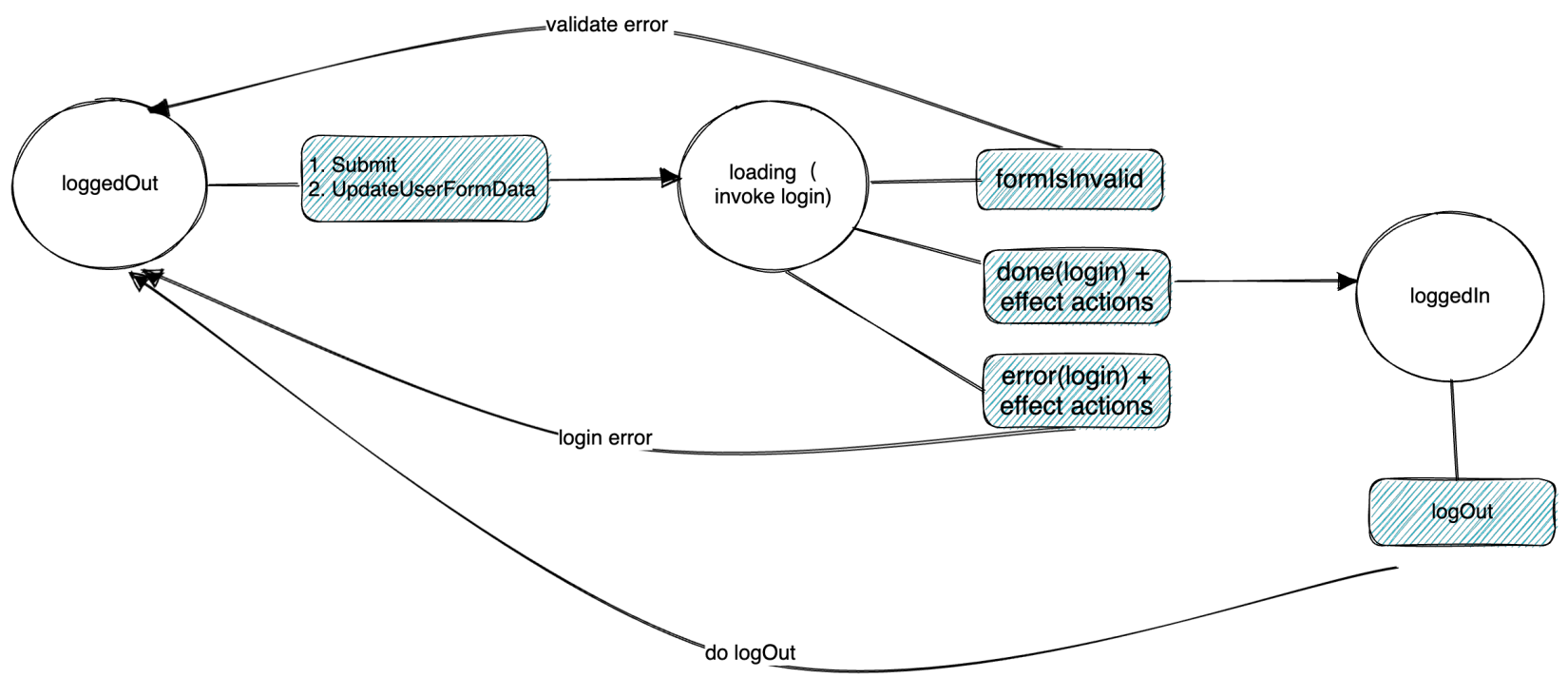
类似这样的状态机的例子数不胜数，甚至于，人也是一种极其复杂的状态机，给定一种刺激或多种刺激组合，也会触发人从某种状态过渡到另一种状态。只不过复杂程度极高，以至于现代科学完全无法解密这种状态机。

有限状态机（FSM）实现原理

具体来说，FSM由以下几部分组成：

初始状态：系统的初始状态。
状态集合：表示系统可能处于的各种状态。
转移函数：定义系统在不同状态之间的转移条件和结果。
终止状态：系统在某个状态下可以停止计算。

有限状态机(FSM) 的实现基于状态转移图。状态转移图 是一个有向图，它表示有限状态机(FSM) 中状态之间的转移关系。在状态转移图中，每个状态表示系统的某种状态，每个转移表示系统从一个状态转移到另一个状态的条件和结果。

实现简易的有限状态机（FSM）

实现步骤

当状态机开始执行时，它会自动进入初始化状态（initial state）。
每个状态都可以定义，在进入（onEnter）或退出（onExit）该状态时发生的行为事件（actions），通常这些行为事件会携带副作用（side effect）。
每个状态都可以定义触发转换（transition）的事件。
转换定义了在退出一个状态并进入另一个状态时，状态机该如何处理这种事件。
在状态转换发生时，可以定义可以触发的行为事件，从而一般用来表达其副作用。

状态转移图

file

function createMachine(stateMachineDefinition) {const machine = {value: stateMachineDefinition.initialState,performTransition(currentState, event) {const currentStateDefinition = stateMachineDefinition[currentState];const destinationTransition = currentStateDefinition.transitions[event];if (!destinationTransition) {return;}const destinationState = destinationTransition.target;const destinationStateDefinition =stateMachineDefinition[destinationState];destinationTransition.action();currentStateDefinition.actions.onExit();destinationStateDefinition.actions.onEnter();machine.value = destinationState;return machine.value;},};return machine;
}const machine = createMachine({initialState: "off",off: {actions: {onEnter() {console.log("off: onEnter");},onExit() {console.log("off: onExit");},},transitions: {switch: {target: "on",action() {console.log('transition action for "switch" in "off" state');},},},},on: {actions: {onEnter() {console.log("on: onEnter");},onExit() {console.log("on: onExit");},},transitions: {switch: {target: "off",action() {console.log('transition action for "switch" in "on" state');},},},},
});let state = machine.value;
console.log(`current state: ${state}`);
state = machine.performTransition(state, "switch");
console.log(`current state: ${state}`);
state = machine.performTransition(state, "switch");
console.log(`current state: ${state}`);

有限状态机（FSM）的应用实现

在状态比较多的情况下，把状态、事件及 transitions 集中到一个状态机中，进行统一管理。这样不需要写太多的 if-else，或者 case 判断，如果增加状态和事件，也便于代码的维护和扩展。

文本解析器

实现思路

确定状态和输入
在编写 FSM 之前，我们需要确定我们的状态和输入。在这个例子中，我们将定义三个状态：起始状态、数字状态和字符串状态。我们还将定义四个输入：数字、字母、引号和空格。
定义状态机类
现在，我们可以编写代码来实现我们的 FSM 。我们需要定义一个状态机类，它将接受输入，并根据转移规则转换状态。该类应该包含以下属性：
- currentState：当前状态。
- states：状态列表。
- transitions：转移列表。
  它还应该包含以下方法：
- transition：该方法接受一个输入参数 input，根据当前状态以及输入参数，执行相应的状态转换。
定义转移规则
我们还需要定义状态之间的转移规则。为此，我们将使用转移列表，其中包含状态之间的映射和输入。转移规则应该考虑当前状态和输入，并根据它们确定下一个状态。如果当前状态和输入没有匹配的转移规则，则应该抛出一个异常。
解析文本
现在，我们可以使用状态机解析文本。我们需要将文本拆分为单词，并将每个单词作为输入提供给状态机。在处理完所有输入后，我们可以通过调用 getInputType 方法来获取解析的令牌。

示例代码

const STATES = {START: "start",NUMBER: "number",STRING: "string",
};const INPUTS = {NUMBER: "number",LETTER: "letter",SPACE: "space",QUOTE: "quote",
};const TRANSITIONS = [{currentState: STATES.START,input: INPUTS.NUMBER,nextState: STATES.NUMBER,},{currentState: STATES.START,input: INPUTS.LETTER,nextState: STATES.STRING,},{ currentState: STATES.START, input: INPUTS.SPACE, nextState: STATES.START },{ currentState: STATES.START, input: INPUTS.QUOTE, nextState: STATES.STRING },{currentState: STATES.NUMBER,input: INPUTS.NUMBER,nextState: STATES.NUMBER,},{ currentState: STATES.NUMBER, input: INPUTS.SPACE, nextState: STATES.START },{currentState: STATES.STRING,input: INPUTS.LETTER,nextState: STATES.STRING,},{ currentState: STATES.STRING, input: INPUTS.SPACE, nextState: STATES.START },{ currentState: STATES.STRING, input: INPUTS.QUOTE, nextState: STATES.START },
];class TextParse {constructor() {this.currentState = STATES.START;this.buffer = "";this.type;}performTransition(input) {const transition = TRANSITIONS.find((t) => t.currentState === this.currentState && t.input === input.type);if (!transition)throw new Error(`Invalid input "${input.value}" for state "${this.currentState}"`);this.currentState = transition.nextState;if (this.currentState === STATES.START) {const token = this.buffer;const type = this.type;this.buffer = "";this.type = "";return {type,value: token,};} else {this.buffer += input.value;this.type = input.type;}}
}function textParse(input) {const textParse = new TextParse();const tokens = [];for (let i = 0; i < input.length; i++) {const char = input[i];try {const token = textParse.performTransition({type: getInputType(char),value: char,});if (token) {tokens.push(token);}} catch (e) {console.error(e.message);return null;}}const lastToken = textParse.performTransition({ type: INPUTS.SPACE });if (lastToken) {tokens.push(lastToken);}return tokens;
}function getInputType(char) {if (/[0-9]/.test(char)) {return INPUTS.NUMBER;} else if (/[a-zA-Z]/.test(char)) {return INPUTS.LETTER;} else if (/[\s\n\t\r]/.test(char)) {return INPUTS.SPACE;} else if (char === '"') {return INPUTS.QUOTE;} else {throw new Error(`Unknown input type for "${char}"`);}
}// Example usage:
console.log(textParse('123 abc "def ghi" 456')); 
// [
//   { type: 'number', value: '123' },
//   { type: 'letter', value: 'abc' },
//   { type: 'letter', value: '"def' },
//   { type: 'letter', value: 'ghi' },
//   { type: '', value: '' },
//   { type: 'number', value: '456' }
// ]

示例代码

web 应用

使用 有限状态机（FSM） 结合 React 构建 web 应用，不局限于身份认证，登录，步骤表单，有蛮多 web 应用在
有限状态机（FSM）的实践 ，下面主要描述 从有限状态机（FSM）在服务端拉取数据的状态转移上的应用

状态转移图
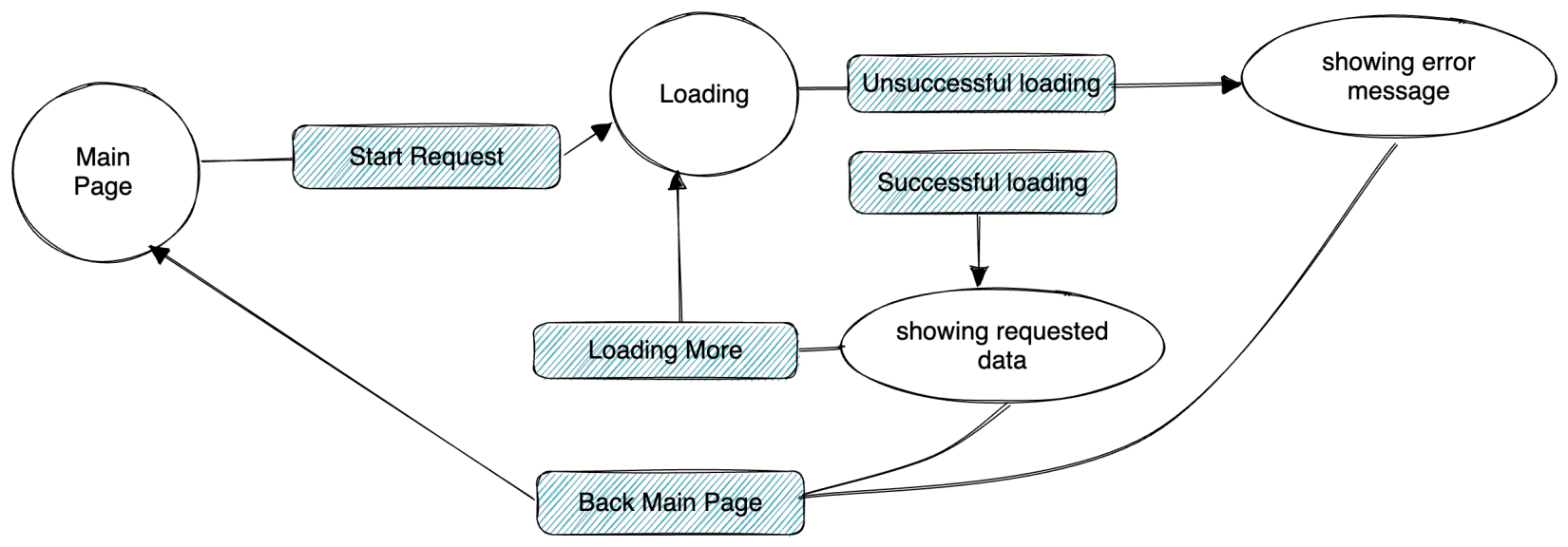
状态集（States）, 转换规则（Transitions）

const states = {INITIAL: "idle",LOADING: "loading",SUCCESS: "success",FAILURE: "failure",
};

const transitions = {[states.INITIAL]: {fetch: () => /* Returns states.LOADING */,},[states.LOADING]: {},[states.SUCCESS]: {reload: () => /* Returns states.LOADING */,clear: () => /* Returns states.INITIAL */,},[states.FAILURE]: {retry: () => /* Returns states.LOADING */,clear: () => /* Returns states.INITIAL */,},
}

示例代码

总结

结合前端应用的探索体现的不多，可以再作为第二篇内容去探讨，有兴趣的同学可以尝试一下 有限状态机（FSM） 在 web 上的应用探索，以及 Xstate库（FSM封装的功能性库） 的应用，以及跟 状态管理库 差异化的知识。在这里提醒一点，状态管理库 （Redux） 和 Xstate 并不是互斥的，Xstate 关注的是如何设计状态，状态管理库关注的是如何管理状态。事实上，状态机几乎可以与任何无主见的状态管理工具一起使用。我鼓励您探索各种方法，以确定最适合您、您的团队和您的应用程序的方法。