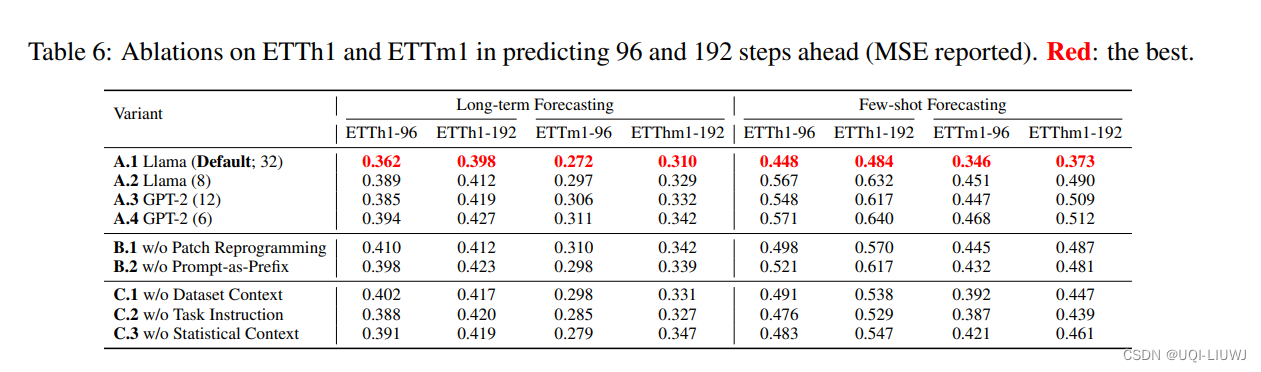
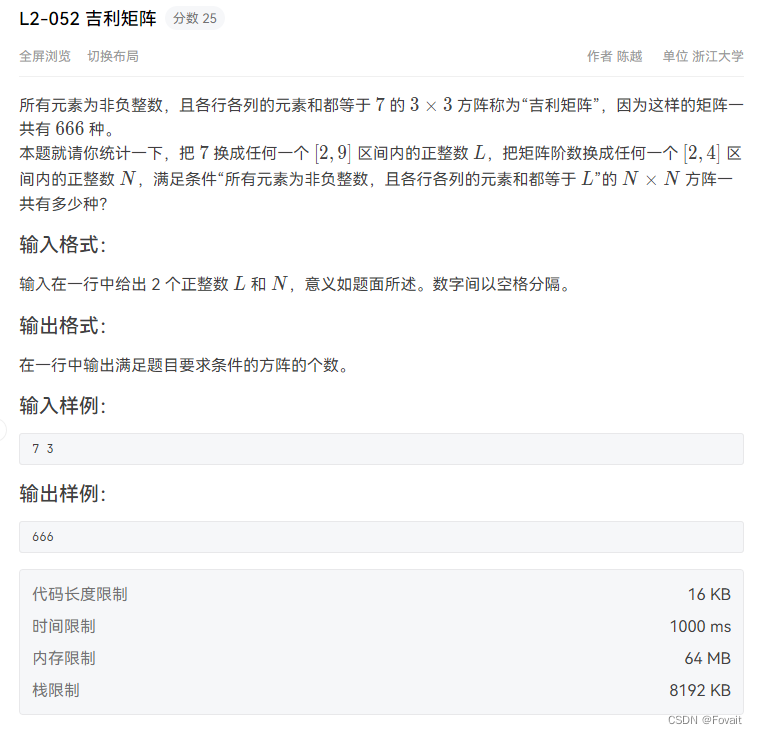
题目
解析
这题考的是搜索剪枝
可行性剪枝:
即判断当前行(列)是否已经超过L和剩下的格子都填最大值是否小于L,若是则剪枝。
当前行数大于1时,判断上一个填完的行是否等于L,若否,则剪枝。
当前行为最后一行,且当前列大于1时,判断上一个填完的列是否等于L,若否,则剪枝。
当前列大于1时,判断上一个列填的数是否大于L,若是则剪枝。
优化顺序剪枝:
从大到小枚举当前填的数
当前格子能填的最大数为min(L-当前行已经填的数,L-当前列已经填的数)
代码
#include <bits/stdc++.h>using i64 = long long;
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int L, n;cin >> L >> n;vector<int> row(n), col(n); int down = 0, up = L;function<i64(int, int)> dfs = [&] (int x, int y) -> i64 {if (x == n) {return int(row[n - 1] == L && col[n - 1] == L);}if (row[x] > L || row[x] + (n - y) * up < L || col[y] > L || col[y] + (n - x) * up < L) return 0;if (x > 0 && row[x - 1] != L) return 0;if (x == n - 1 && y > 0 && col[y - 1] != L) return 0;if (y > 0 && col[y - 1] > L) return 0;i64 r = 0;for (int i = min(L - col[y], L - row[x]); i >= 0; i--) {row[x] += i;col[y] += i;r += dfs(x + ((y + 1) / n), (y + 1) % n);row[x] -= i;col[y] -= i;}return r;};cout << dfs(0, 0) << '\n';return 0;
}