2024华东杯数学建模邀请赛B题:建立车辆转向与几何约束优化模型
完整论文和代码下载:↓↓↓
https://www.yuque.com/u42168770/qv6z0d/bnnv13hz319fokwe
本文文章较长,建议先目录。经过不懈的奋战,目前我们已经完成了2024华东杯数学建模竞赛B题的30页完整论文和代码,部分图片如下:

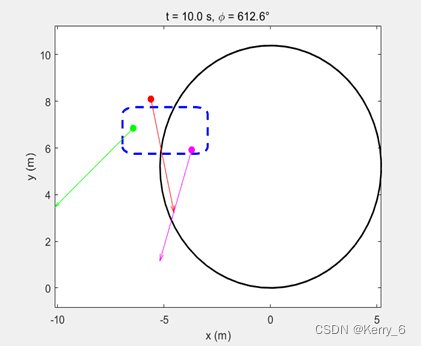



问题1的分析
问题1要求我们建立描述四轮车辆转弯运动的数学模型。首先,我们需要分析车辆转弯时的受力情况和运动特点。通过受力分析,可以得到车辆的横向和横摆运动方程。同时,我们还需要考虑车辆的转向机构和轮胎特性对车辆转弯性能的影响。
接下来,我们要选择合适的坐标系和状态变量来描述车辆系统。一般采用车辆固连坐标系和地面坐标系,状态变量包括车辆质心位置、横摆角、质心侧偏角等。通过引入适当的简化假设,如忽略悬架运动、轮胎侧偏力线性化等,我们可以得到一个相对简单而又能反映车辆转弯特性的"自行车"模型。
最后,根据车辆受力图和运动方程,我们可以建立起车辆转弯运动的状态空间方程。该方程通常是一个非线性微分方程组,需要数值积分求解。同时,我们还需要考虑一些约束条件,如轮胎侧偏角不能过大、车身侧倾角不能过大等,以确保模型在实际工况下的适用性。通过对模型进行标定和验证,我们最终可以得到一个较为准确和全面的车辆转弯运动数学模型。
## 问题2的分析
问题2是一个直接应用问题1建立的数学模型进行仿真计算的问题。首先,我们需要根据题目给定的车辆参数和初始工况,确定模型中的各项参数取值,如车辆质量、转动惯量、轮胎侧偏刚度等。同时,我们还需要将题目要求的转弯工况转化为控制量,如转向盘转角、车速等。
然后,我们可以利用MATLAB等数学工具,对问题1建立的车辆转弯运动微分方程组进行数值求解。一般采用龙格-库塔法、欧拉法等常见的数值积分算法。通过迭代计算,我们可以得到车辆质心和四个车轮在转弯过程中的位置坐标。为了提高计算效率和精度,我们需要合理选择积分步长和误差控制参数。
最后,我们要将计算得到的车辆运动轨迹以合适的形式保存到文件中,并绘制直观的可视化图形。通过对仿真结果进行分析和讨论,我们可以评估车辆的转弯性能,预测车辆在极限工况下的行驶安全性和稳定性。同时,仿真结果也为车辆转向系统的设计和调校提供了重要的依据和参考。
## 问题3的分析
问题3是一个车辆低速转弯通过性评估的问题。我们需要分析车辆在狭窄空间内完成转弯动作所需的最小转弯半径。首先,我们要明确影响车辆转弯通过性的关键因素,如车辆前后悬长度、轴距、车身宽度等几何参数,以及转向系统的特性参数,如转向盘转角与前轮转角的传动比、前轮最大转角等。
接下来,我们可以利用平面几何关系,推导出车辆在给定转向角下的转弯轨迹方程。通常假设车辆低速行驶时,转弯半径由车辆内前轮的转向角决定。通过分析车身边缘轮廓与车位边界的几何关系,并考虑适当的安全裕度,我们可以得到车辆完成转弯动作所需的最小转弯半径,进而确定车辆前轮的最大转向角。
此外,我们还需要考虑车辆转向时的实际限制因素,如转向机构的物理结构限位、轮胎与地面的附着极限等。这就要求我们在几何分析的基础上,结合车辆动力学特性进行综合评估。例如,我们可以利用多体动力学软件建立整车转向模型,分析转向过程中的轮胎侧偏特性、悬架运动学特性等对车辆转弯轨迹的影响,并优化车辆悬架和转向系统参数,以提高车辆的转弯通过性和操纵稳定性。
(后略,见完整版本)
Matlab 代码实现(部分):
% 参数初始化
L = 4; W = 2; D = 0.6; d = 0.16;
lf = 2-0.5; lr = 2-0.5;
v = 20/3.6; theta = 30/180*pi;dt = 0.1; T = 10; t = 0; phi = 0;
x0 = 0; y0 = 0; % 计算转弯半径与角速度
R = (lf+lr)/tan(theta); omega = v/R;% 计算alpha角
alpha = atan(W/(2*lf))-pi/2;% 初始化保存数据的数组
tArray = []; xcArray = []; ycArray = [];
xfiArray = []; yfiArray = []; xfoArray = []; yfoArray = [];
xriArray = []; yriArray = []; xroArray = []; yroArray = [];
phiArray = []; % 创建动画图窗
figure('Position',[100 100 800 600])% 循环求解
while t <= T% 求解质心位置xc = R*sin(phi); yc = R*(1-cos(phi));% 求解前内轮位置(略,见完整版本)% 求解前外轮位置
(略,见完整版本)% 求解后内轮位置 % 求解后外轮位置xro = xc - lr*sin(alpha); yro = yc - lr*cos(alpha);% 保存当前时刻数据tArray(end+1) = t; xcArray(end+1) = xc; ycArray(end+1) = yc;% 绘制动画clf % 清除之前的图形hold on; box on; axis equalplot(xcArray,ycArray,'k-','LineWidth',1.5) % 车辆质心轨迹% 绘制车辆矩形框rectangle('Position',[xc-L/2 yc-W/2 L W],'Curvature',[0.3 0.3],...'EdgeColor','b','LineWidth',2,'LineStyle','--')% 绘制车轮位置plot(xfi,yfi,'ro','MarkerFaceColor','r')plot(xfo,yfo,'go','MarkerFaceColor','g')
除了绘制的车辆质心和四个车轮的轨迹图之外,我们还可以考虑以下几种可视化方式:绘制车辆矩形边框在不同时刻的位置和方向,直观显示车辆转弯过程、绘制车轮速度矢量,反映车轮的速度大小和方向、绘制车辆横摆角随时间的变化曲线,反映车辆转弯过程中角度的变化。为了绘制动态的车辆转弯动画,我们可以在while循环内调用pause函数,让程序暂停一段时间,并在每次暂停时更新车辆位置和方向,从而生成动画效果。
Matlab代码首先初始化了题目给定的已知参数,然后计算转弯半径R、角速度omega和前轮中心到车头方向的夹角alpha。在while循环内部,(见完整版本)
完整论文和代码下载:↓↓↓
https://www.yuque.com/u42168770/qv6z0d/bnnv13hz319fokwe





![ES 深度分页问题及针对不同需求下的解决方案[ES系列] - 第509篇](https://img-blog.csdnimg.cn/img_convert/de9dbf52fee84ed2aeeef803d166404e.png)
