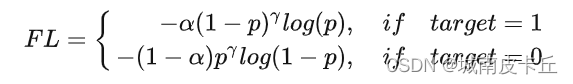深度学习快速入门系列---损失函数-编程知识

在深度学习中，损失函数的作用是量化预测值和真实值之间的差异，使得网络模型可以朝着真实值的方向预测，损失函数通过衡量模型预测结果与真实标签之间的差异，反映模型的性能。同时损失函数作为一个可优化的目标函数，通过最小化损失函数来优化模型参数。在本篇文章中，我们介绍一下，深度学习中最常用的几种损失函数：

一、适用于回归问题的损失函数

1、L1 LOSS

2、L2 LOSS

3. smooth L1 loss

二、适用于分类问题的损失函数

1、交叉熵损失函数

2、Binary Cross-Entropy 交叉熵损失

3、Focal Loss

一、适用于回归问题的损失函数

1、L1 LOSS

L1损失函数也叫作平均绝对误差（MAE），它是一种常用的回归损失函数，是目标值与预测值之差绝对值的和，表示了预测值的平均误差幅度，而不需要考虑误差的方向。总的来说，它把目标值与估计值的绝对差值的总和最小化。L1 LOSS的数学公式为：

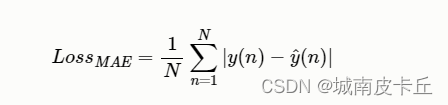
下面演示，在pytorch中使用该函数：

import torch
import torch.nn as nnpredict=torch.randn(2,3);
target=torch.randn(2,3)print("predict:{}".format(predict))
print("target:{}".format(target))#方式一：使用Pytorch内置函数
loss1_fn=nn.L1Loss()
loss1=loss1_fn(predict,target)print("loss1:{}".format(loss1))#方式二：自己按照L1公式实现函数
loss2_fn=torch.abs(target-predict)
loss2=torch.mean(loss2_fn)print("loss2:{}".format(loss2))

从控制台可以看到，使用pytorch内置的L1函数与我们自己实现的L1函数结果相同。

2、L2 LOSS

也被称为均方误差（MSE, mean squared error），它把目标值与估计值的差值的平方和最小化。其数学公式为：

下面在pytorch中实现MSE损失函数:

import torch
import torch.nn as nn
predict=torch.rand(2,3)
target=torch.rand(2,3)
#使用pytroch内置
loss1_fn=nn.MSELoss()
loss1=loss1_fn(predict,target)
print(loss1)
#自己按照公式实现
loss2_var=predict-target
loss2_var=loss2_var**2
loss2=torch.mean(loss2_var)
print(loss2)

3. smooth L1 loss

在提到smooth L1 loss之前，很有必要提一下L1、L2损失函数的优缺点：

L1损失函数的导数公式如下：

在这里插入图片描述

L2损失函数的导数公式如下：

在这里插入图片描述

smooth L1的公式(其中公式中的x表示，预测值与真实值的差值的绝对值)

smooth L1的导数：

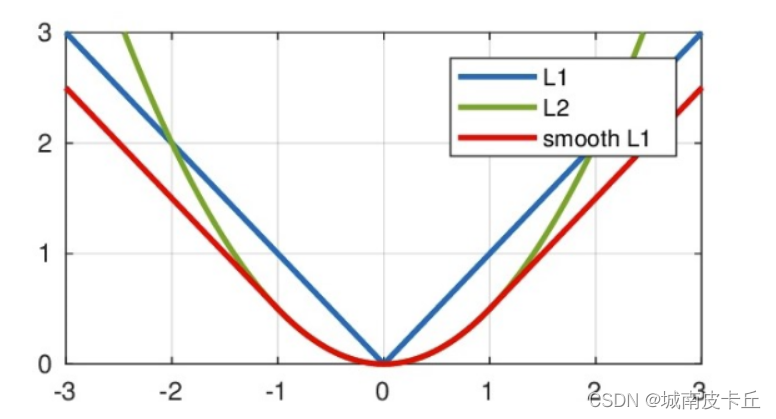
从上图中可以看出L1损失函数具有如下优缺点：

优点：无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解
缺点：在中心点是折点，不能求导，梯度下降时要是恰好学习到w=0就没法接着进行了

L2损失函数：

优点：各点都连续光滑，方便求导，具有较为稳定的解
缺点：不是特别的稳健，因为当函数的输入值距离真实值较远的时候，对应loss值很大在两侧，则使用梯度下降法求解的时候梯度很大，可能导致梯度爆炸

尽管L1收敛速度比L2损失函数要快，并且能提供更大且稳定的梯度，但是L1有致命的缺陷：导数不连续，导致求解困难，在训练后期损失函数将在稳定值附近波动，难以继续收敛达到更高精度。这也导致L1损失函数极其不受欢迎。使用MAE损失（特别是对于神经网络来说）的一个大问题就是，其梯度始终一样:

这意味着梯度即便是对于很小的损失值来说，也还会非常大，会出现难以收敛的问题；而 MSE 当损失变小的时候，梯度也会变小，从而更容易收敛
为了修正这一点，我们可以使用动态学习率，它会随着我们越来越接近最小值而逐渐变小。
在这种情况下，MSE会表现的很好，即便学习率固定，也会收敛。MSE损失的梯度对于更大的损失值来说非常高，当损失值趋向于0时会逐渐降低，从而让它在模型训练收尾时更加准确

而Smooth L1 Loss 是在 MAE 和 MSE 的基础上进行改进得到的；在 Faster R-CNN 以及 SSD 中对边框的回归使用的损失函数都是Smooth L1 作为损失函数。

仔细看上面的图像，smooth L1各点连续，在x较小时，对x的梯度也会变小，x很大时，对x的梯度的绝对值达到上限1，也不会太大导致训练不稳定。smooth L1避开L1和L2损失的缺陷

公式以及图像中可以看出，Smooth L1 Loss 从两个方面限制梯度：

当预测框与 ground truth 差别过大时，梯度值不至于过大，防止梯度爆炸；
当预测框与 ground truth 差别很小时，梯度值足够小，有利于收敛；

Smooth L1 的优点是结合了 L1 和 L2 Loss：

相比于L1损失函数，可以收敛得更快；
相比于L2损失函数，对离群点、异常值不敏感，梯度变化相对更小，训练时不容易跑飞

下面在pytorch中实现smooth L1损失函数：

import torch
import torch.nn as nnpredict=torch.randn(2,3)
target=torch.randn(2,3)loss1_fn=nn.SmoothL1Loss()
loss1=loss1_fn(predict,target)
print(loss1)def smooth_l1_loss(x,y,beta=1):diff=torch.abs(x-y)loss2=torch.where(diff<beta,0.5*diff**2/beta,diff-0.5*beta)return loss2.mean()
loss2=smooth_l1_loss(predict,target)
print(loss2)

二、适用于分类问题的损失函数

1、交叉熵损失函数

交叉熵损失函数（Cross-Entropy Loss Function）一般用于分类问题。假设样本的标签y ∈ {1, · · · C}为离散的类别，模型f(x, θ) ∈ [0, 1] 的输出为类别标签的条件概率分布，即

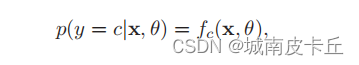
并满足

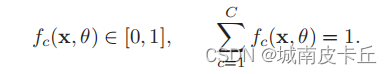
我们可以用一个C 维的one-hot向量y来表示样本标签。假设样本的标签为k，那么标签向量y只有第k 维的值为1，其余元素的值都为0。标签向量y可以看作是样本标签的真实概率分布，即第c维（记为yc，1 ≤ c ≤ C）是类别为c的真实概率。假设样本的类别为k，那么它属于第k 类的概率为1，其它类的概率为0。对于两个概率分布，一般可以用交叉熵来衡量它们的差异。标签的真实分布y和模型预测分布f(x, θ)之间的交叉熵为：

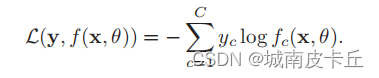
比如对于三类分类问题，一个样本的标签向量为y = [0, 0, 1]T，模型预测的标签分布为f(x, θ) = [0.3, 0.3, 0.4]T，则它们的交叉熵为：

因为 y 为 one-hot 向量，因此交叉熵损失函数公式也可以写为：

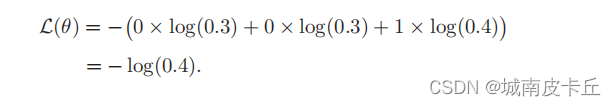
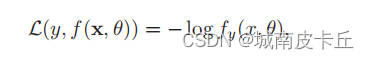
其中fy(x, θ)可以看作真实类别y 的似然函数。因此，交叉熵损失函数也就是负对数似然损失函数（Negative Log-Likelihood Function）。

import randomimport torch
import torch.nn as nn
predict=torch.randn(2,3)
#随机生成标签
target=torch.tensor([random.randint(0,2) for _ in range(2)],dtype=torch.long)
# print(target)
#方式一：使用torch中定义好的函数
loss_fn=nn.CrossEntropyLoss()
loss=loss_fn(predict,target)
print(loss)
#方式二：自己按照公式实现
def cross_entropy_loss(predict,label):prob=nn.functional.softmax(predict,dim=1)log_prob=torch.log(prob)label_view=label.view(-1,1)loss=-log_prob.gather(1,label_view)loss_mean=loss.mean()return loss_mean
loss2=cross_entropy_loss(predict,target)
print(loss2)

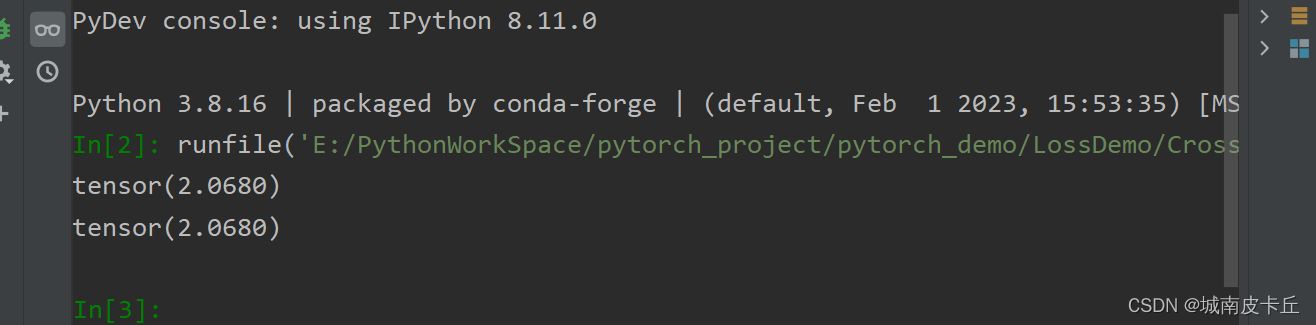
2、Binary Cross-Entropy 交叉熵损失

Binary Cross-Entropy 交叉熵损失用于二分类问题，它其实就是交叉熵损失函数（Cross-Entropy Loss Function）的特例，也就是将多分类任务的特例化，变成二分类任务。这里不在做赘述。

3、Focal Loss

该损失函数由《Focal Loss for Dense Object Detection》论文首次提出，当时提出的背景是为了解决目标检测领域的突出问题：

Two-stage 的目标检测算法准确率高，但是速度比较慢；One-stage 的目标检测算法速度虽然快很多，但是准确率比较低

想要提高 One-stage 方法的准确率，就要找到其原因，作者提出的一个原因就是正负样本不均衡

Focal loss 损失函数是为了解决 one-stage 目标检测中正负样本极度不平衡的问题；
- 目标检测算法为了定位目标会生成大量的anchor box
- 而一幅图中目标(正样本)个数很少，大量的anchor box处于背景区域(负样本)，这就导致了正负样本极不平衡
two-stage 的目标检测算法这种正负样本不平衡的问题并不突出，原因：
- two-stage方法在第一阶段生成候选框，RPN只是对anchor box进行简单背景和前景的区分，并不对类别进行区分
- 经过这一轮处理，过滤掉了大部分属于背景的anchor box，较大程度降低了anchor box正负样本的不平衡性
- 同时在第二阶段采用启发式采样(如：正负样本比1：3)或者OHEM进一步减轻正负样本不平衡的问题
One-Stage 目标检测算法，不能使用采样操作
- Focal loss 就是专门为 one-stage 检测算法设计的，将易区分负例的 loss 权重降低
- 使得网络不会被大量的负例带偏

focal loss，是在标准交叉熵损失基础上修改得到的。这个函数可以通过减少易分类样本的权重，使得模型在训练时更专注于难分类的样本。为了证明focal loss的有效性，作者设计了一个dense detector：RetinaNet，并且在训练时采用focal loss训练。实验证明RetinaNet不仅可以达到one-stage detector的速度，也能有two-stage detector的准确率。在了解该损失函数的公式之前先了解一下在分类问题中常用到的交叉熵函数，交叉熵公式可以表示为：

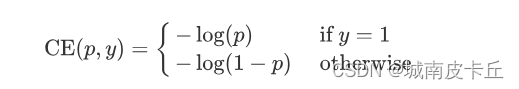
为了方便，将交叉熵公式写为：

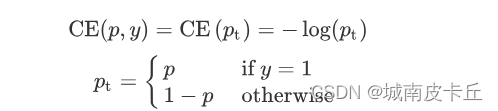
为了解决正负样本不平衡的问题，我们通常会在交叉熵损失的前面加上一个参数 $\alpha$ ：

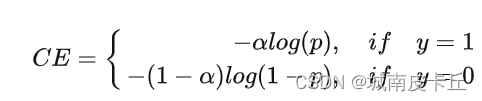
既然在 One-stage 方法中，正负样本不均衡是存在的问题，那么一个比较常见的算法就是给正负样本加上权重：增大正样本的权重，减小负样本的权重

通过设定 $\alpha$ 的值来控制正负样本对总的 loss 的共享权重;上面的方法虽然可以控制正负样本的权重，但是无法控制容易分类和难分类样本的权重。因此就设计了 Focal Loss。其公式为：

其中

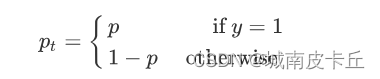
$\gamma$ 为常数，称之为 focusing parameter ( $\gamma$ ≥ 0)，当 $\gamma$ =0 时，Focal Loss 就与一般的交叉熵损失函数一致； $(1-p_{t})^{\gamma }$ 称之为调制系数，目的是通过减少易分类样本的权重，从而使得模型在训练时更专注于难分类的样本。当 $\gamma$ 取不同的值，Focal Loss 曲线如下图所示，其中横坐标是 $p_{t}$ 纵坐标是 loss

通过 $\gamma$ 参数，解决了难易样本分类的难题，但是我们通常还会在Focal Loss 的公式前面再加上一个参数 $\alpha$ 用于解决正负样本不平衡的问题：

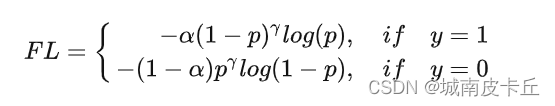
实验表明 $\gamma$ 取2, $\alpha$ 取0.25的时候效果最佳。

Focal Loss实现：

def py_sigmoid_focal_loss(pred,target,weight=None,gamma=2.0,alpha=0.25,reduction='mean',avg_factor=None):pred_sigmoid = pred.sigmoid()target = target.type_as(pred)pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)focal_weight = (alpha * target + (1 - alpha) *(1 - target)) * pt.pow(gamma)loss = F.binary_cross_entropy_with_logits(pred, target, reduction='none') * focal_weightloss = weight_reduce_loss(loss, weight, reduction, avg_factor)return loss

这个代码很容易理解，先定义一个pt：

然后计算：

focal_weight = (alpha * target + (1 - alpha) *(1 - target)) * pt.pow(gamma)

也就是这个公式：

然后再把BCE损失*focal_weight