碎碎念：实习过程中发现在进行雷达知识交流时，大部分同事都会用英文简称代替中文的一些称呼，比如Chirp、FFT等等。起初我觉得是因为很多英伟达、TI芯片的开发教程都是英文的，所以看得多了大家都习惯这样称呼，后来在和指导我的前辈交流时发现是因为国内对于一个步骤都有很多称呼，比如说我们接下来讲的快时间傅里叶变换又称为距离维傅里叶变换，慢时间傅里叶变换又称为速度维傅里叶变换，但他们的英文专有名称只有一个，分别是Range FFT和Doppler FFT。用英文称呼的原因更是为了精确性，也不用让大家记那么多名词。同时前辈也告诫我在学习时候不要怕麻烦，要把每一个缩写的全程都要标注好记忆好，才能对于系统更加熟悉。

引入

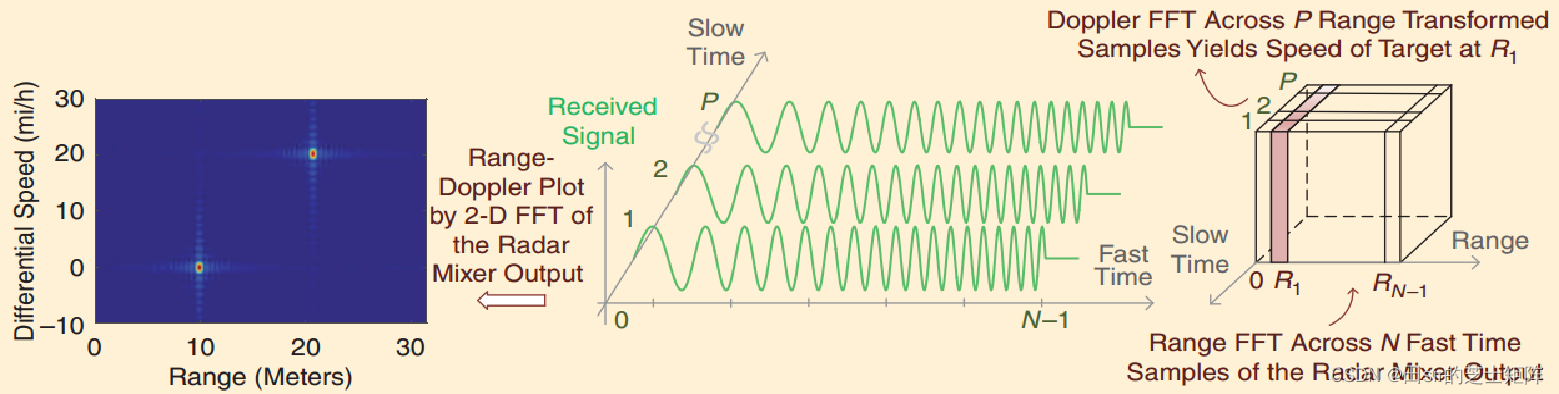
毫米波雷达系列文章中我们一再强调的是时刻关注我们的“目录”，也就是我们的框架，那我们来看一下快时间与慢时间傅里叶变化在雷达处理流程的哪一步：

图中可以发现快时间傅里叶变换（又称距离FFT，Range FFT）在ADC采样结束后，毫米波雷达进一步讲快时间傅里叶变换后的数据进行慢时间傅里叶变换（又称二维FFT，Doppler FFT）。

那我们需要来想象一下ADC采样后的数据是什么样的呢？

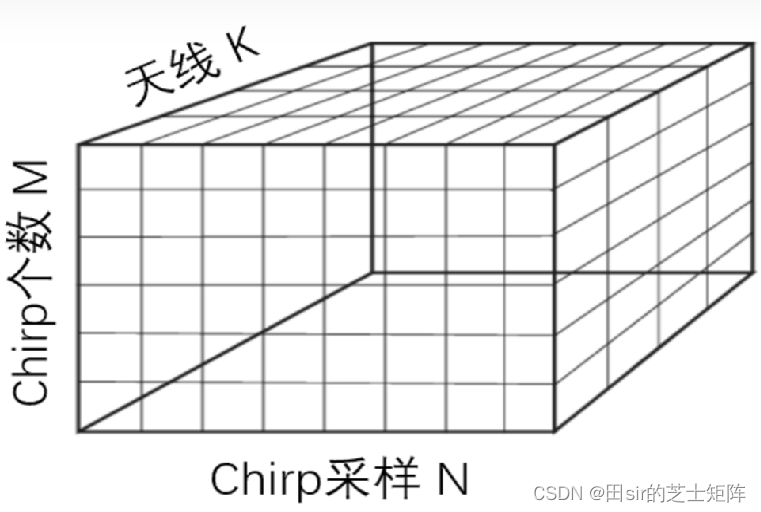
信号通过ADC采样后会得到一个由chirp采样点、采样个数以及通道/天线数组成的三维数据块（Radar Data Cube）。得到的数据仍然是离散的时域信号点，我们需要通过傅里叶变换求得频谱图，从而求得目标的距离信息以及速度信息。

 

 

原理推导

这里会先推导RFFT与DFFT共性的原理，在各自的部分会进行进一步推导：

天线发射信号与接收信号进行混频滤波后，可以表示为：

 其中K代表FM调制常数（也就是时频图的斜率），代表差频（即IF信号的频率），n代表采样点，代表单个chirp中的采样率，代表单个chirp周期。根据：

可以将采样后的信号表示为：

此时的信号中含有参数时间差及差频，故可进一步通过傅里叶变换求解这两个参数。

快时间傅里叶变换（Range FFT）

我们认为在一个chirp周期中，由于电磁波的速度极快的特性，所以时间是非常短的，也就是时间很“快”。同时也可以将目标对象在快时间内的移动近似没有，所以在快时间维度来看，目标物体几乎“静止”，以快时间为时域的时间维度对信号进行傅里叶变换，其距离也就非常容易测量。

在进行快时间傅里叶变换时，将慢时间看作常数，即仅仅做一个chirp周期内的傅里叶变换（对应于radar cube中的每一行做FFT），即可求得时间差 ，根据：

即可求得对应物体的距离R。

慢时间傅里叶变换（又称二维FFT，Doppler FFT）

 相对于一个chirp周期的时间，不同chirp之间的间隔时长就会相对更“长”，也就是时间会相对更“慢”，以慢时间为时域的时间维度，结合快时间的傅里叶变换我们就可以计算出目标的速度信息。

在进行慢时间傅里叶变换时，将快时间看作常数，以每个chirp间隔作为时间轴进行进行傅里叶变换（对应于radar cube中的每一列再做FFT），对应频谱图中的最高点即为差频fd，根据：

即可求得目标物体的速度信息v。