自动控制原理学习--平衡小车的控制算法（三）-编程知识

上一节PID的simulin仿真，这一节用LQR

一、模型

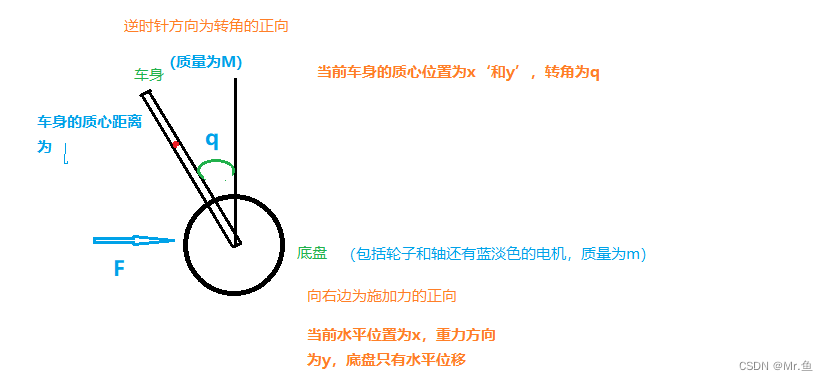
二、LQR

LQR属于现代控制理论的一个很重要的点，这里推荐B站的【Advanced控制理论】课程（up主DR_CAN），讲得很好，这里引用了他视频里讲LQR的ppt。

LQR属于lost优化问题，L：Linear ；Q：Quadratic二次型；R：regulater 调制器

主要是优化状态空间下，保证稳定的同时，如何选取状态方程特征值。

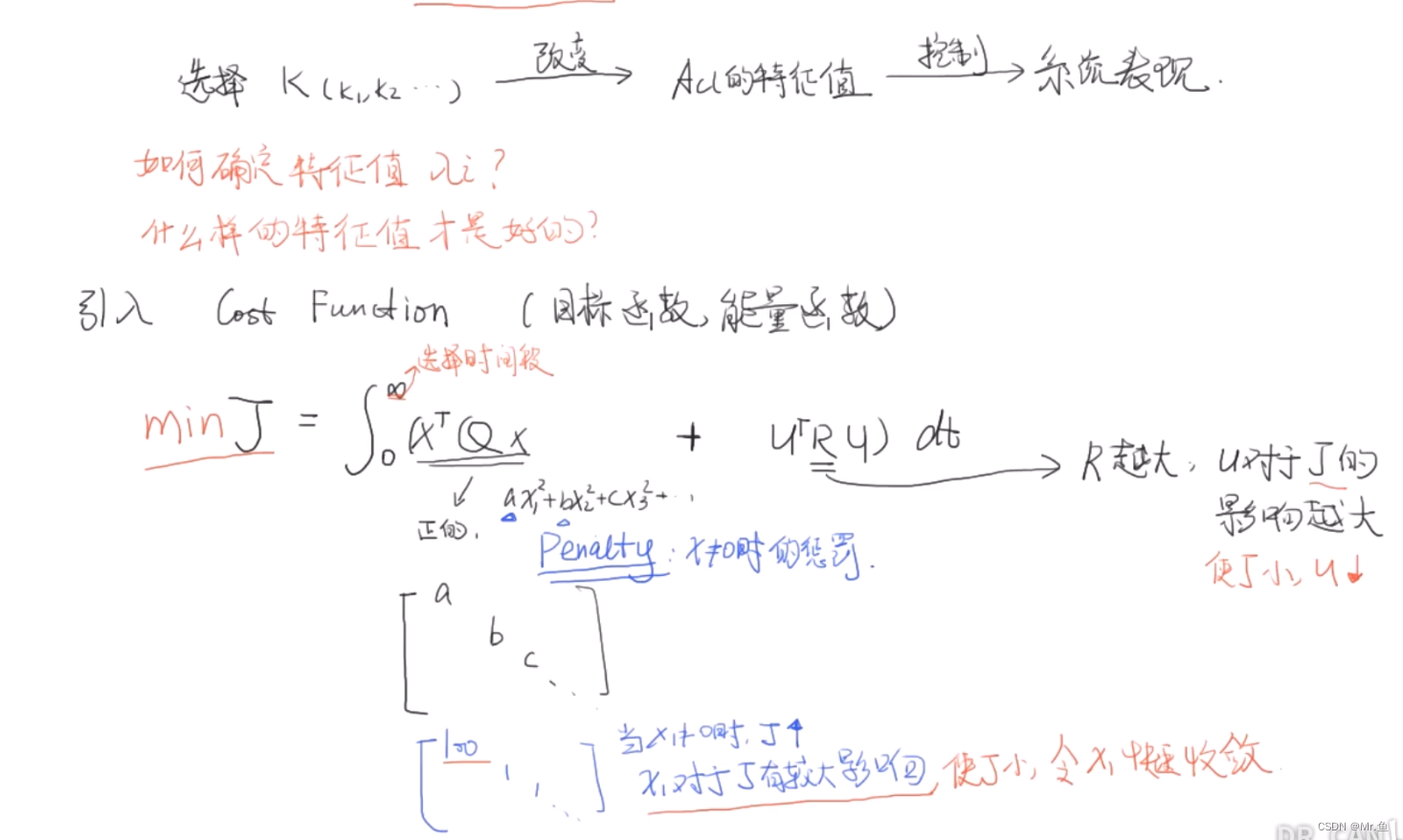
Q一般是根据你想控制那些状态给出不同权重的矩阵，就是一个对角矩阵，按顺序对状态量给出权重，给的数值越大，代表你对对应的状态控制要求也高，R是输入是N*1的矩阵，一般只有一维输入的话就一个数，越大表示对输入的控制要求更高。

二、平衡小车LQR

由于需要有状态转移矩阵和输入系数矩阵，所以需要建立动力学模型，建模方法很多（一般常用的是牛顿力分析和拉格朗日方程）

1.牛顿力学分析方程

（1）底盘只有水平方向的移动，故运动方程只有在x方向，

假设小车的摩擦系数为b,由m*a=F公式可得：

$m \ddot{x}=F-b \dot{x}-N$ 其中N为车身（摆杆）对底盘在x方向的反作用力（1）

（2）车身（摆杆）受力分析：

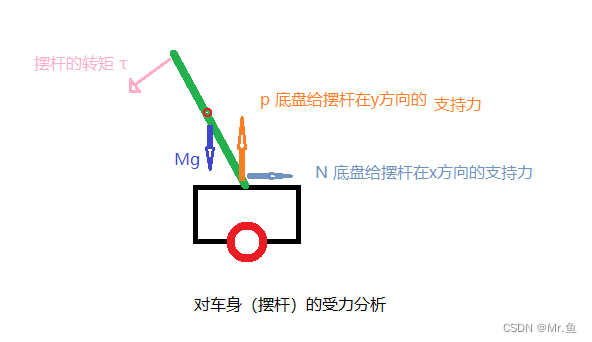
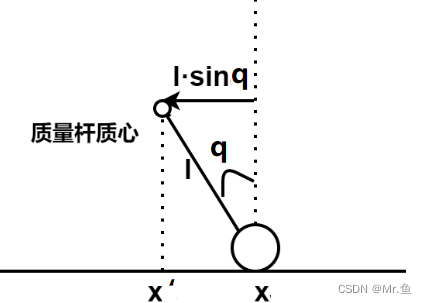
某一时刻单摆在水平上的位置：

$x^{\prime}=x-l \cdot \sin (q)$

单摆在水平方向所收到的力只有N，所以水平方向的运动方程:

$\boldsymbol{M} \ddot{\boldsymbol{x}}^{\prime }=\boldsymbol{N}$

$\boldsymbol{M} \left(\boldsymbol{x}-\boldsymbol{l} \cdot \sin (q)\right)^{\prime \prime}=\boldsymbol{N}$

$N=M \ddot{x}-M l \ddot{q} \cos (q)+M l \dot{q}^{2} \sin (q)$ （2）

由（2）带入（1）可得第一个运动方程

$F=(M+m) \ddot{x}+b \dot{x}-M l \ddot{q} \cos (q)+M l \dot{q}^{2} \sin (q)$ （3）

对单摆在垂直方向的受力分析

$\begin{array}{l} \boldsymbol{M} \ddot{y}^{\prime }=\boldsymbol{P}-\boldsymbol{M} g \\ y= l cos(q)\\ \ddot{y}^{\prime }=-\ddot{q} \sin (q)-\dot{q}^{2} \cos(q) \\ \boldsymbol{M} l\left(-\ddot{q} \sin (q)-\dot{q}^{2} \cos(q)\right)=\boldsymbol{P}-\boldsymbol{M} g \\ \boldsymbol{P} =M g-M l \ddot{q} \sin (q)-M l \dot{q}^{2} {\cos (q)}\end{array}$ （4）

摆杆质心力矩平衡可得( $I$ 是摆杆的转动惯量，规则的物体容易求，但这里我看了人家，尝试去算，但都感觉不对，看过别人的基本设定在0.005左右都可以，后面试了其他值感觉都还可以用，其实有种方法是用实物倒放，让它自由摆动后测出相关的值去推，以后有时间可以试试）：

$P l \sin (q)+N l \cos (q)=I \ddot{q}$ (5)

把公式（2）、（4）带入（5）可得

$\begin{array}{l} M g l \sin (q)-M l \ddot{q} \sin q l \sin q-M l \dot{q}^{2} \cos q l \sin q \\ =M g l \sin q-M l^{2} \ddot{q}+M \ddot{x} l \cos q= I \ddot{q} \end{array}$

化简得到第二条运动学方程：

$\left(I+M l^{2}\right) \ddot{q}-M g l \sin (q)=M l \ddot{x} \cos(q)$ （6）

由（3）和（6）得到的方程组：

$\left\{\begin{array}{l} F=(M+m) \ddot{x}+b \dot{x}-M l \ddot{q} \cos (q)+M l \dot{q}^{2} \sin (q)\\ \\(I+M l^{2}) \ddot{q}-M g l \sin (q)=M l \ddot{x} \cos(q) \end{array}\right.$

线性化, 为小接近的小角度，q为小接近0的小角度， $\dot{q} ^2\approx 0$ , 𝑐𝑜𝑠(q) 为1， 𝑠𝑖𝑛(q) 为0, F施加给小车的输入，改成u表示：

$\left\{\begin{array}{l} u=(M+m) \ddot{x}+b \dot{x}-M l \ddot{q} \\ \\ (I+M l^{2}) \ddot{q}-M g l q=M l \ddot{x} \end{array}\right.$ (7)

(7)可以改写成

$\ddot{x} = \frac {-b(I+M l^2) }{p} \dot{x} +\frac{M^2 g l^2}{p} q +\frac{I+M l^2}{p} u$

$\ddot{q} = \frac {-b M l }{p} \dot{x} +\frac{M g l (M+m)}{p} q +\frac{M l}{p} u$

其中 $p=I(M+m)+ Mml^2$

设状态量为

$\begin{bmatrix} x \\ \dot x \\ q \\ \dot q \end{bmatrix}$

最终的状态空间方程模型为：

$\begin{bmatrix} x \\ \dot x \\ q \\ \dot q \end{bmatrix} =\begin{bmatrix} &0 &1 &0 &0 \\ & 0 & \frac{-b(I+M l^2)}{p} & \frac{M^2gl^2}{p} &0 \\ & 0 &0 &0 &1 \\ &0 & \frac{-bMl}{p} & \frac{Mgl(M+m)}{p} &0 \end{bmatrix} * \begin{bmatrix} x \\ \dot x \\ q \\ \dot q \end{bmatrix} +\begin{bmatrix} 0\\ \frac{I+M l^2}{p} \\ 0 \\ \frac{Ml}{p} \end{bmatrix} *u$

状态转移矩阵A 输入矩阵B

由于状态量与输出反馈一致，故C矩阵为

$C=\begin{bmatrix} 1 & 0& 0&0 \\ 0& 1& 0&0 \\ 0& 0& 1&0 \\ 0& 0& 0& 1 \end{bmatrix}$ 如果你模型里面反馈数据只有平移速度和角度速度，那C就算2*4的矩阵

D=0

有了A B C D矩阵就可以用LQR求解（也可以用MPC来求解，套路都一样），MATLAB里面有lqr的求解器，一行代码搞定.

不过还有Q 和R 超参的设置， Q可简单设置[10 0 10 0] 顺序对应的水平方向的x 和速度，角度q 和角速度，意思是对x 和角度q重点控制， R=1，对输入要求一般，都可以修改，根据具体情况修改超参。

MALAB 的代码很简单

K = lqr(A,B,Q,R)

会得出K，K 是4*1的向量，然后分别与状态量点乘就得到输入u的值，即F 这就是控制量

由于系统是非时变系统，因此lqr只需求一次K就行了

通过A 和B矩阵，也可以判断系统是否可控

Tc = ctrb(A,B);
if (rank(Tc)==4)fprintf('此系统是可控的！\n');

如果不加外力，系统肯定是不稳定的，直接用

Tc = ctrb(A);
if (rank(Tc)==4)fprintf('此系统是可控的！\n');

就可以测试，

说白就算去判断它的状态转移矩阵是否满秩，现代控制理论有相关的推导分析

simulink建模跟上一张PID的模型基本一样，只是计算输入控制量这块不一样，简单放个图：

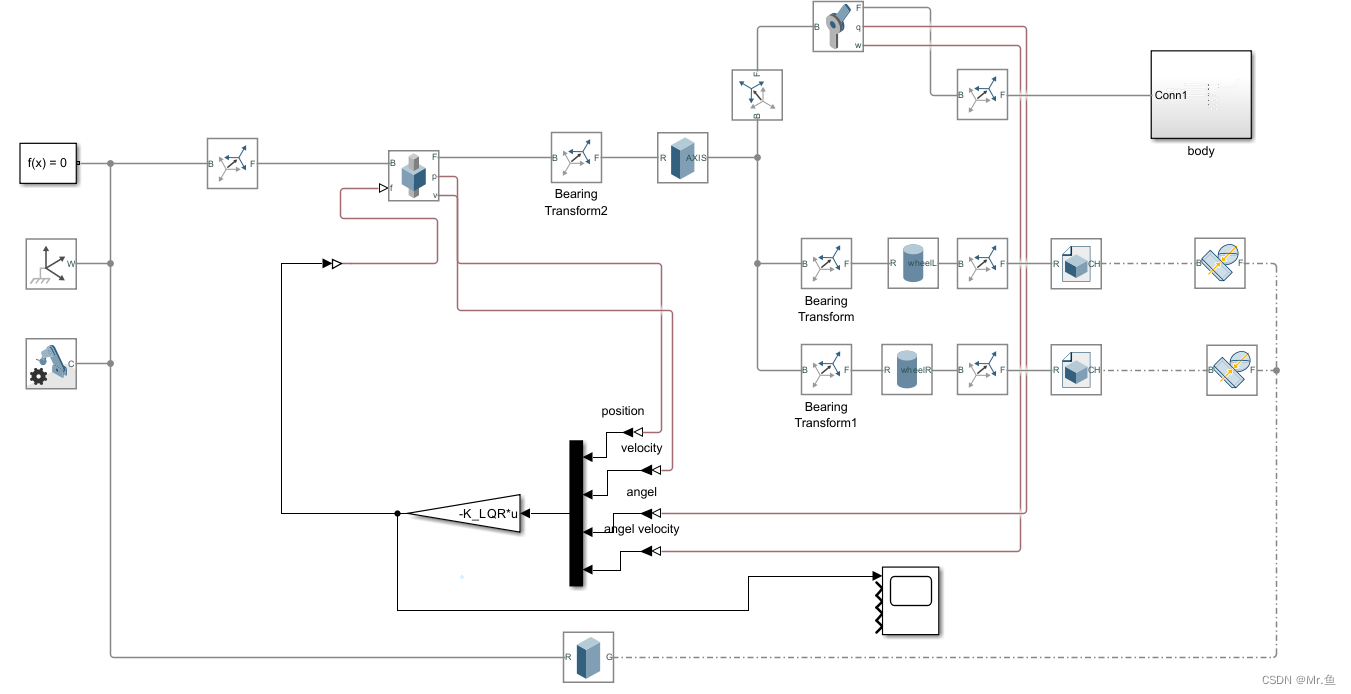
这里的K_LQR就算lar算出来的K，这里是负反馈，因此是负号；

其他的参数主要有 $l$ 取0.065m；g=9.8，车身质量M=1.25kg，底盘m=0.5kg。

算出的K为

K =[ -1.0000 -2.1447 37.5875 3.2123 ]

三、上面的牛顿力学分析运动方程很繁琐，同样是找状态转移矩阵 A 输入矩阵 B 一般直接用拉格朗日动力学方程，省事些。

这里不想再敲公式了，直接参考使用B站博主（J_H_Li）的小车倒立摆最优控制教程视频讲得通俗易懂，推荐去看

拉格朗日方程：

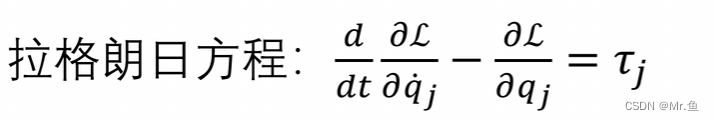
$q_j$ 是指某个状态量 $\tau$ 是对应 $q_j$ 状态量的外力

分别找出系统总动能和势能再分别对状态量进行拉格朗日方程

总动能

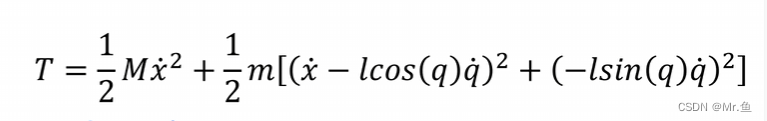
因为以底盘质点为原点，只有车身的势能，因此总势能

$V=mgl cos(q)$

这里的M是底盘的质量，m是摆杆的，

所以拉格朗日量

分别对x和q进行拉格朗日方程得到：

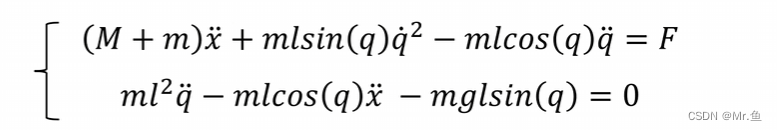
再进行线性化，q为小接近0的小角度， $\dot{q} ^2\approx 0$ , 𝑐𝑜𝑠(q) 为1， 𝑠𝑖𝑛(q) 为0, 得到两条动力方程：

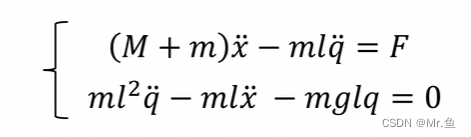
然后退出A B矩阵，F改为u，就得到

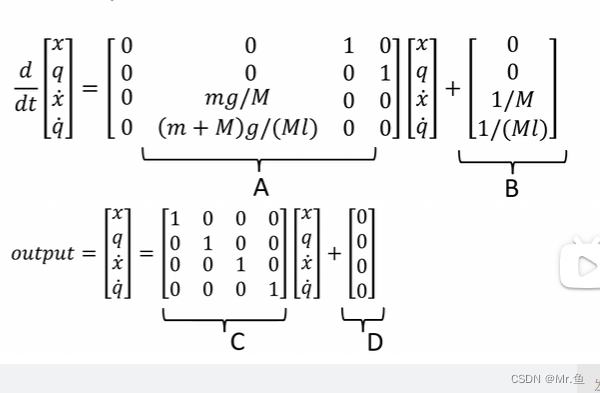
可以看到A 和 B 跟上面用牛顿受力分析得出的不一样，这里算出来的k

K =[ -1.0000 -1.9719 36.2409 1.8586 ]

但相差不大，都是可以让系统稳定的

这种方法比牛顿受力分析，找出一大堆公式要友好得多。

自动控制原理学习--平衡小车的控制算法（三）

三、上面的牛顿力学分析运动方程很繁琐，同样是找状态转移矩阵 A 输入矩阵 B 一般直接用拉格朗日动力学方程，省事些。

相关文章

k8s概述及核心组件

手机视频提取gif怎么操作？分享这个方法不能错过！

每日Attention学习4——Spatial Attention Module

迅睿CMS中实现关键词搜索高亮

3D点云处理的并行化

【python】模块与包

Java基础编程(高级部分)

「Java开发指南」如何用MyEclipse搭建GWT 2.1和Spring？（一）

图神经网络的应用领域

Elasticsearch的基本使用

小结3：英语泛读

聊天框 - 微信加载历史数据的效果原来这样实现的