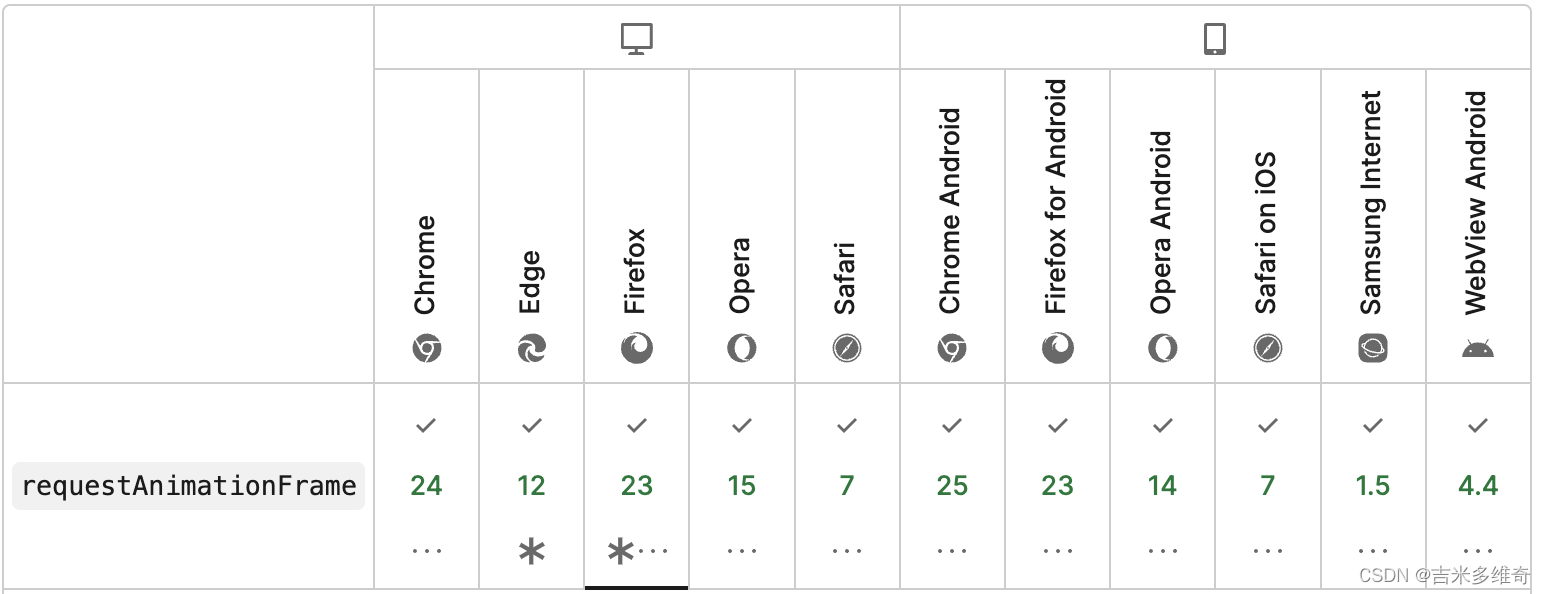
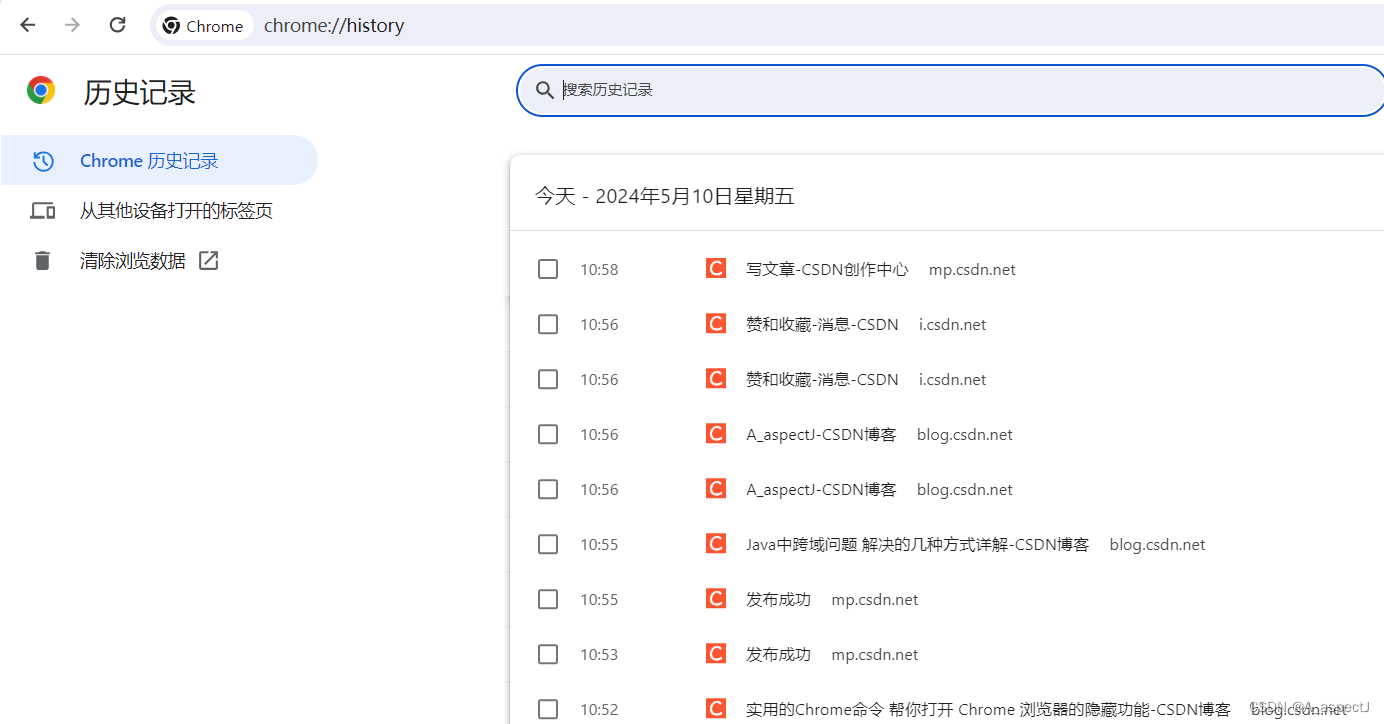
之前对于环的解释，不太行，这里我给出进一步地说明。

首先对环的解释:  我这里说的环指的是频域段中的ai变化的时候对图像像素的变化的极大的影响程度的环状效果，会出现不规则的环状的提亮或增暗的效果。实际上是每个fj都有影响，但是极大影响会出现环状效果。

假设ai都相同的时候，而符号只与j有关，所以可以设为a，傅里叶变换公式可以写为:fj=，a为ai取同一个值。,这里的j已经是逆序过,写为j-。

1.,这个简化的公式可以估计，修改低频区域的ai的时候，图像的低位区没有环效果，因为低位区的高位都是0，高位区域有环效果，因为高位有值为1，那么可以使用附近的概念，就是将高位的某一位置换为1或者0，置换为1是升位，置换为0是降位。这可以看做是从高位区从低到高顺序或者是高到低的顺序，结果是一样的。我从低到高来看，图像高位区越低，环之间的距离越大，距离是2的指数倍数的。考虑在接近图像最右下的位置，环的圈数就变大了。环没有中心，因为改的是一大片频率域中的低频区ai，非要说的话，我只能说环的内部在图像的低位区。最小环经过图像中心处。

因为是估算，ai是各不相同的，那么应该是图像中心处附近是最小的环了，之后向外部辐射出去，一层层的距离变大了，并且靠近图像中心的环变化最不明显，越外层越明显，具体我下面举例解释

具体的解释是: 以一维图像点列为例100...0的最近位置是100..1，但是1无影响，不管。有影响是100..01....xxxx，但是逆序之后发现是最小相位值，那么影响最小，所以形成第一个环。第二个环是100..11....xxxx，影响第二大，所以是形成第二个环。第三个环是第二个环是100..111....xxxx，这就发现环之间的距离是在远离中心之后增大的，但是强度是越来越大的，原因是环状效果是极大值，而环内变化是差不多的。比如第二个环和第三个环之间的内部在100..11....xxxx和100..111....xxxx之内，比较差异，发现不明显，所以没有环没有累加效果。那么环增大变化效果明显的原因是第三个环的逆序之后的1有更大的相位角，对fj的影响更大 。

2.,现在估计修改高频区域的ai的值（我这里的修改ai的值指的是增大，因为如果减小的话，就是模糊了，应该可能看到，模糊看的话，应该效果更好，因为没有噪点了。）

图像的任意二进制位的低位有值，那么都会有附近的概念，那么也就有环效果。但是这个环效果最差，因为频率的低位区是容易影响fj的值的，高频区域是最难影响的。至于环的内部如果是以图像xxx10..00开始的，这很难说清楚内部。那么只能把这个时候的环定义修改了。之前定义内部为低位区，是为了看起来是环基本上是凸的，现在还是为了看起来是基本上是凸的，只能把内部定义为形如xxxx11..1的形式，其实内部是高频区域的位置的逆序。但是逆序之后不连续啊。（之前改低频逆序之后是高位，局部是连续的。）这样就行成了许多个环带，而且每个环带只有一个中心位置，（而修改低频只有一个环带，没有具体的中心点，只有中心区域），这种不连续的后果是，分散的各个位置作为环的中心的时候，环带的强弱是不同的，而且，每个环带上，靠近中心的环强度越弱（而之前靠近中心区域的环强度也是越弱的），环带远离中心点，环之间的距离越大（而之前是远离中心区域环带的距离越大）。但不是高频区的每个位置都是环的中心，具体解释在下面的例子中。

还是举例解释：以一维图像点列为例xx...100..0, 其中xx...是高位区，100..0是低位区，的最近位置是xx...100..1，会产生第一个环，强度最弱，距离最近。第二个附近位置是xx...100..11，产生第二个环，强度比第一个增强了一倍（因为逆序之后对应的频率更低了，有大相位角产生了比较明显的fj变化），距离变大了，可以看得出来xx...100..11也在高频区，但不是这个环的中心，而在环上了。

总结：修改高频区域的ai，会产生多个环带，并且环之间的距离和强度是随着远离中心指数递增的。但是都非常弱。

修改低频区域，会产生一个大环带，并且环之间的距离和强度是随着远离中心区域指数递增的。而且都非常强。

3.,现在讨论修改中频的ai的时候，

至于修改中频区域，应该是在这两种之间，首先大环带的中心区域在低频区，但是大环带的范围在图像的位置某个高处，就没有了，不会向之前修改低频的那样环带到达了图像的最右下位置。

然后是小环带，因为频率为000...1xxx1..xx，所以图像的某些位置也没有小环带， 某些位置是平均分布的，所以可以看做是从高频修改的状态，均匀剔除这些环带的。

然后把这两种情况得到的环带组合起来就是修改中频的环带效果。

说实话，我下载了camera raw13版本之后并未观察到在图像中有任何的环。那么我写错了？感觉不合理啊，因为附近的概念是真实的，附近变化是最大的，也没问题，所以环上的变化率达到了极大值也是没问题的啊，难道是因为环周围的变化率接近所以观察不到了？这还真有可能。所以这个环的效果不是明暗的局部最大，而是膨胀收缩环，局部膨胀最大？环之间的像素都收缩了，环附近的像素在膨胀？环中心区域的像素没有收缩和膨胀变化，就是普通变化。膨胀的意思是相当于拿了放大镜观看了。收缩是相当于用缩小镜观看了。

还是有问题，我认为膨胀收缩也不对，应该是观察到了复空间上的值。因为图像是在实数空间的，但是傅里叶变换是在复数空间的，所以，所谓的膨胀就是一个位置j，其实如果把整个ai看做是活动的话，应该在j处，有个复数空间，图像只取了复数空间上的实轴上的值，膨胀的效果是将j位置的复数空间的某个值旋转到实轴上之后，映射到了j的附近处。我认为就是将j的复数空间展开了一部分铺在了图像j的邻域上，这里的附近是平面，跟二进制无关。而原来的像素被挤走了，要膨胀就需要收缩，肯定也有收缩中心，不管了，为了编一个谎言，我又要编另一个谎言，虽然感觉是没错的，但是我写不下去了。所以增强对比度和平滑的图像边缘是收缩中心？

我的结论是傅里叶变换，修改频率域的任何值，都会对图像表面产生扭曲的效果。这种扭曲是一圈一圈的带状，像是奇怪透镜的扭曲一样。其中修改高频区的ai，最不明显，修改低频区的ai最明显。

晚上重写一下，我确信我之前写的低频的举例没有问题。

继续讨论低频的情况，为什么使用了camera raw没有达到我期待的呢？

100..010..00，其中100..01是高位，0..00是低位，全为0，他的相邻的两个位置是

100..001..11和100..010..01。100..001..11逆序之后，有一个改变量就是最低位，但是我需要的改变量的变化，100..001..11和前面的位置100..001..10的改变量的绝对值是一样的。而100..010..01和之后位置100..010..10的改变量的绝对值也是一样的。

而100..001..11和100..010..00，明显改变量提升了。100..010..00和100..010..01的改变量也是一样的。

这说说明了，在我说的环中的一个点100..010..00，和环内的最近的像素相比变化是陡增的，这种陡增跟像素本身的灰度级无关，而跟空间域图像的位置有关，位置都是确定的。难道需要仅需图像混合处理？我试试ps的混合处理看看结果。先试试A-B。

这个问题真的很奇怪，我在ps中的混合模式做了，没有任何发现。我发现图像本身有噪声，会干扰，为了去除噪声，我使用负移动，结果还是没有发现任何的条纹，我已经放大图像的像素到最大了，没有任何发现。

于是我使用了填充颜色的图像，结果发现使用清晰度居然不改变图像的值，如果清晰度的公式是修改傅里叶变换的ai的值，那么图像的值肯定会变化的，所以是实现的公式跟我的不一样。

我的一切的推导没有任何问题，但是居然和camera raw的结果不一致，我认为是camera raw的实现公式有问题，没有使用傅里叶变换。

一切基于傅里叶变换的公式都会形成环，至于是不是明暗相间的条纹，感觉可能性不大，因为明显图像不可能是这样的。我称这个环是位置噪声，跟位置有关，但是大小跟图像本身的灰度级有关。我感觉之所以没有出现，应该是早就注意到了这个问题，难道是截取函数？跟卷积有关的那个函数，反傅里叶变换之后确实是无限长的。这个问题就不管了，很可能是同一个问题我重新做了表述。