2024年4月12日饿了么春招实习试题【第二题:魔法师】-题目+题解+在线评测【二分】
- 题目描述:
- 输入格式
- 输出格式
- 样例输入
- 样例输出
- 评测数据与规模
- 解题思路一:
- 解题思路二:
- 解题思路三:动态规划
题目描述:
塔子哥是一名魔法师,他有一个由 n 个正整数组成的魔法序列 A。现在他想对这个序列施展魔法,每次施展魔法会给出三个正整数 l,r,k,塔子哥想知道在区间 [l,r] 中是否存在一个位置 i,使得将区间 [l,i] 中的所有数进行按位或运算的结果等于 k。如果存在,输出满足条件的最小的 i,否则输出 −1。
输入格式
第一行包含两个正整数 n,Q,表示魔法序列的长度和施展魔法的次数。
第二行包含 n 个正整数 A1,A2,…,An,表示魔法序列 A。
接下来 Q 行,每行包含三个正整数 l,r,k,表示一次魔法的施展。
输出格式
对于每次施展魔法,输出一行一个整数,表示答案,如果不存在满足条件的位置则输出 −1。
样例输入
5 5
3 2 3 3 6
1 2 3
1 5 7
1 4 7
2 2 2
2 3 7
样例输出
1
5
-1
2
-1
评测数据与规模
1 ≤ n , Q ≤ 1 0 6 , 1 ≤ l ≤ r ≤ n , 0 ≤ A _ i , k < 2 30 。 1 \le n,Q \le 10^6,1 \le l \le r \le n,0 \le A\_i, k < 2^{30}。 1≤n,Q≤106,1≤l≤r≤n,0≤A_i,k<230。
OJ链接:
https://codefun2000.com/p/P1817
解题思路一:

import sys
input = lambda : sys.stdin.readline().strip()
n,q = map(int, input().split())
a = list(map(int, input().split()))
lb = [None] * (n + 1)
d = dict()
for i in range(n-1,-1,-1):d[a[i]] = i + 1nd = {}for k, v in d.items():nd[k|a[i]] = min(nd.get(k|a[i],n),v)d = ndlb[i + 1] = d.copy()
for _ in range(q):l,r,k = map(int, input().split()) if k not in lb[l] or r < lb[l][k]:print("-1")else:print(lb[l][k])时间复杂度:O(nlogU + 1)
空间复杂度:O(nlogU)
解题思路二:
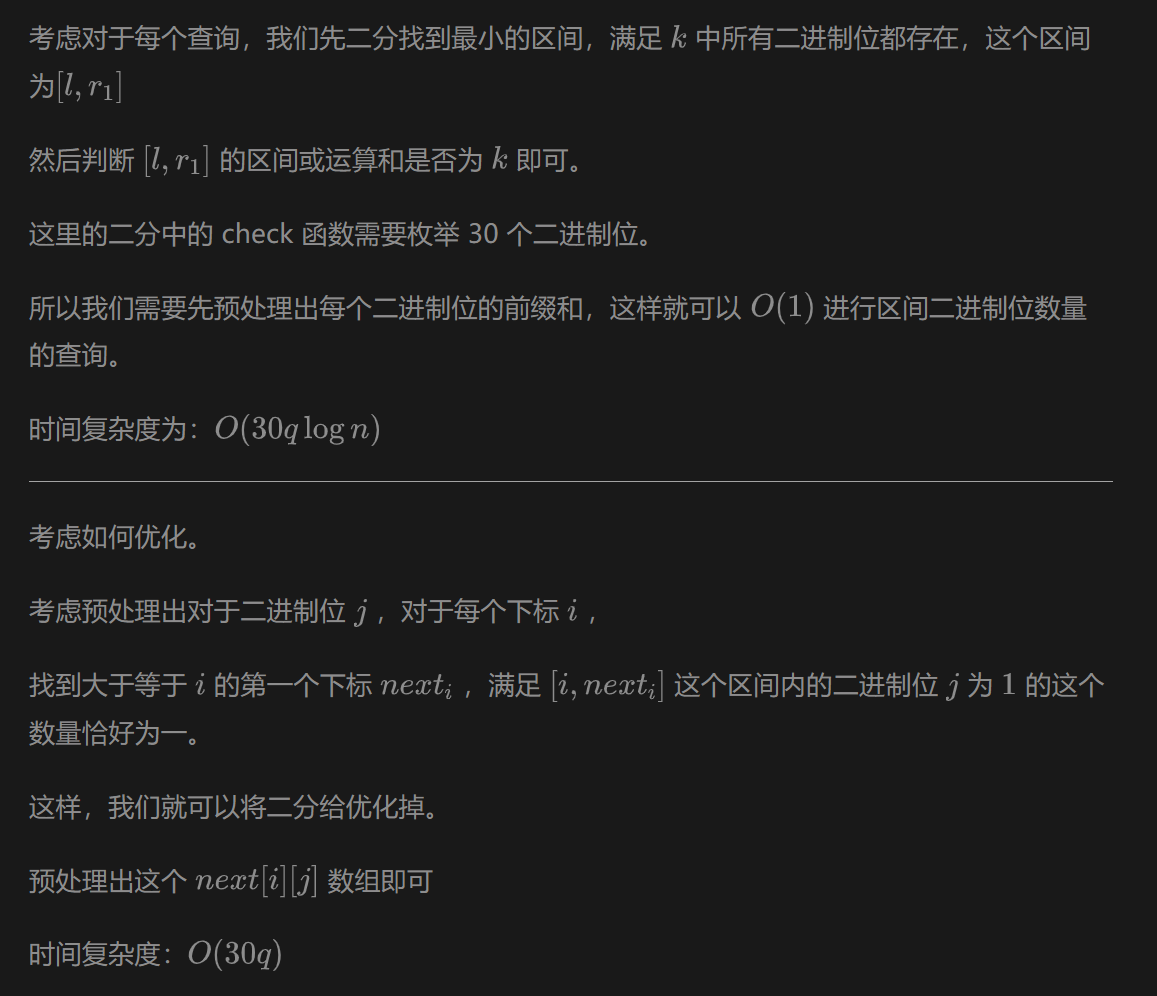
n, q = map(int, input().split())
a = list(map(int, input().split()))MAXBIT = 30
MAXV = 2**30 - 1
pre = [[0 for _ in range(MAXBIT)] for i in range(n + 1)]
for i in range(1, n + 1):for j in range(MAXBIT):pre[i][j] = pre[i - 1][j]if a[i - 1] >> j & 1:pre[i][j] += 1for i in range(q):l, r, k = map(int, input().split())if k > MAXV:print(-1)continuekbit = [0] * MAXBITfor j in range(MAXBIT):kbit[j] = k >> j & 1left, right = l, rwhile left < right:mid = (left + right) >> 1ok = Truefor j in range(MAXBIT):if kbit[j] == 1 and pre[mid][j] - pre[l - 1][j] == 0:ok = Falsebreakif ok:right = midelse:left = mid + 1ok = Truefor j in range(MAXBIT):if kbit[j] == 1 and pre[right][j] - pre[l - 1][j] == 0:ok = Falsebreakif kbit[j] == 0 and pre[right][j] - pre[l - 1][j] > 0:ok = Falsebreakif ok:print(right)else:print(-1)n, q = map(int, input().split())
a = list(map(int, input().split()))MAXBIT = 30
MAXV = 2**30 - 1
pre = [[0 for _ in range(MAXBIT)] for _ in range(n + 1)]
nxt = [[-1 for _ in range(MAXBIT)] for _ in range(n + 1)]
for i in range(1, n + 1):for j in range(MAXBIT):pre[i][j] = pre[i - 1][j]if a[i - 1] >> j & 1:pre[i][j] += 1for j in range(MAXBIT):for i in range(n, 0, -1):if a[i - 1] >> j & 1:nxt[i][j] = ielif i < n:nxt[i][j] = nxt[i + 1][j]for i in range(q):l, r, k = map(int, input().split())if k > MAXV:print(-1)continueok = Truepos = lfor j in range(MAXBIT):if k >> j & 1:if nxt[l][j] == -1 or nxt[l][j] > r:ok = Falsebreakpos = max(pos, nxt[l][j])if ok:v = 0for j in range(MAXBIT):if pre[pos][j] - pre[l - 1][j] > 0:v |= 1 << jif v != k:ok = Falseelse:print(pos)if not ok:print(-1)时间复杂度:O(n)
空间复杂度:O(30q)
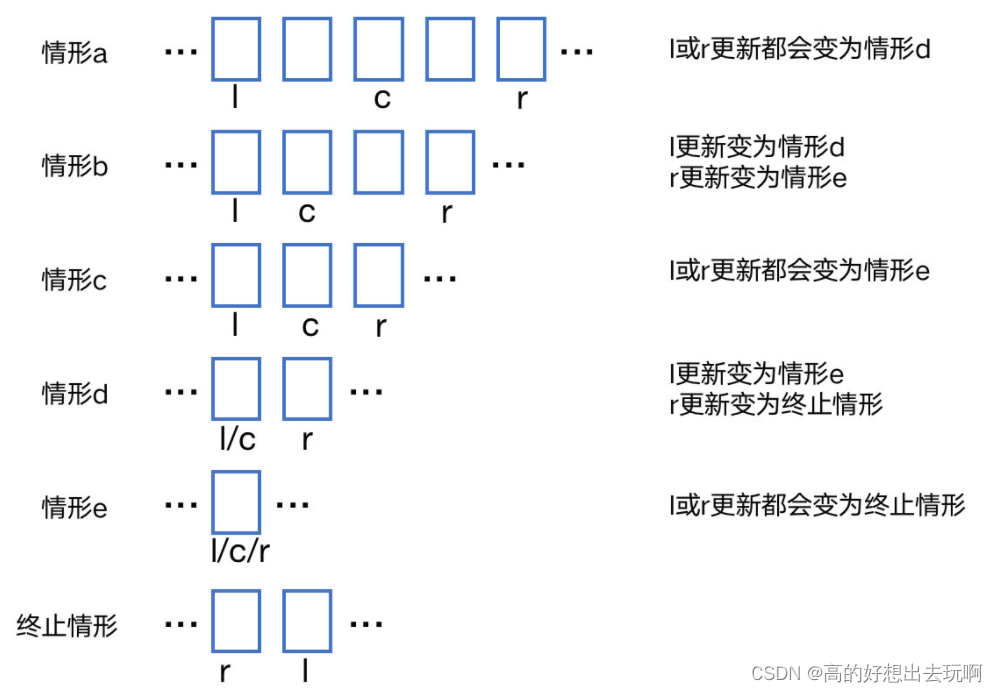
解题思路三:动态规划
n, q = map(int, input().split(' '))
f = [[n] * 30 for _ in range(n + 1)]
a = list(map(int, input().split(' '))) + [0]
for i in range(n - 1, -1, -1):for j in range(30):f[i][j] = i if (a[i] >> j & 1) == 1 else f[i + 1][j]
while q > 0:q -= 1l, r, k = map(int, input().split(' '))l, r = l - 1, r - 1mx, mn = -1, nfor j in range(30):if (k >> j & 1) == 1:mx = max(mx, f[l][j])else:mn = min(mn, f[l][j])if mx <= r and mx < mn:print(mx + 1)else:print(-1)
时间复杂度:O(n)
空间复杂度:O(n)