探索数据结构：堆的具体实现与应用-编程知识

✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 堆的概念

堆(Heap)是计算机科学中一类特殊的数据结构。堆通常是一个可以被看作一棵完全二树的数组对象，若满足：

任意节点的值>=其子节点的值。则称为大根堆。
任意节点的值<=其子节点的值。则称为小根堆。

2. 堆的实现方式

虽然堆是一种特殊的二叉树，它既可以用数组存储也可以用链式存储。但是考虑到其完全二叉树的特性，我们最好采用数组存储的方式，因为这样既方便访问，也并不会浪费格外的空间。

假设某个合法下标为i：

若双亲节点存在，下标为(i-1)/2。
若孩子节点存在，左孩子下标为2i+1，右孩子为2i+2。

3. 堆的功能

堆的初始化。
堆的插入。
堆的删除。
获取堆顶的元素。
堆的元素个数。
堆的判空。
输出堆。
建堆。
销毁堆。

4. 堆的声明

因为我用数组实现堆，所以堆的声明与顺序表类似。

typedef int HpDataType;
typedef struct Heap 
{HpDataType* a;//存储数据int size;//大小int capacity;//容量
}Heap;

5. 堆的实现

5.1. 堆的初始化

5.1.1. 代码实现

void HeapInit(Heap* hp)//堆的初始化
{assert(hp);hp->a = NULL;hp->size = hp->capacity = 0;
}

5.1.2. 复杂度分析

时间复杂度：没有额外的时间消耗，时间复杂度为O(1)。
空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5.2. 堆的插入

当我们堆进行插入时可能会破坏堆的原有结构，这时就需要我们对其进行向上调整。

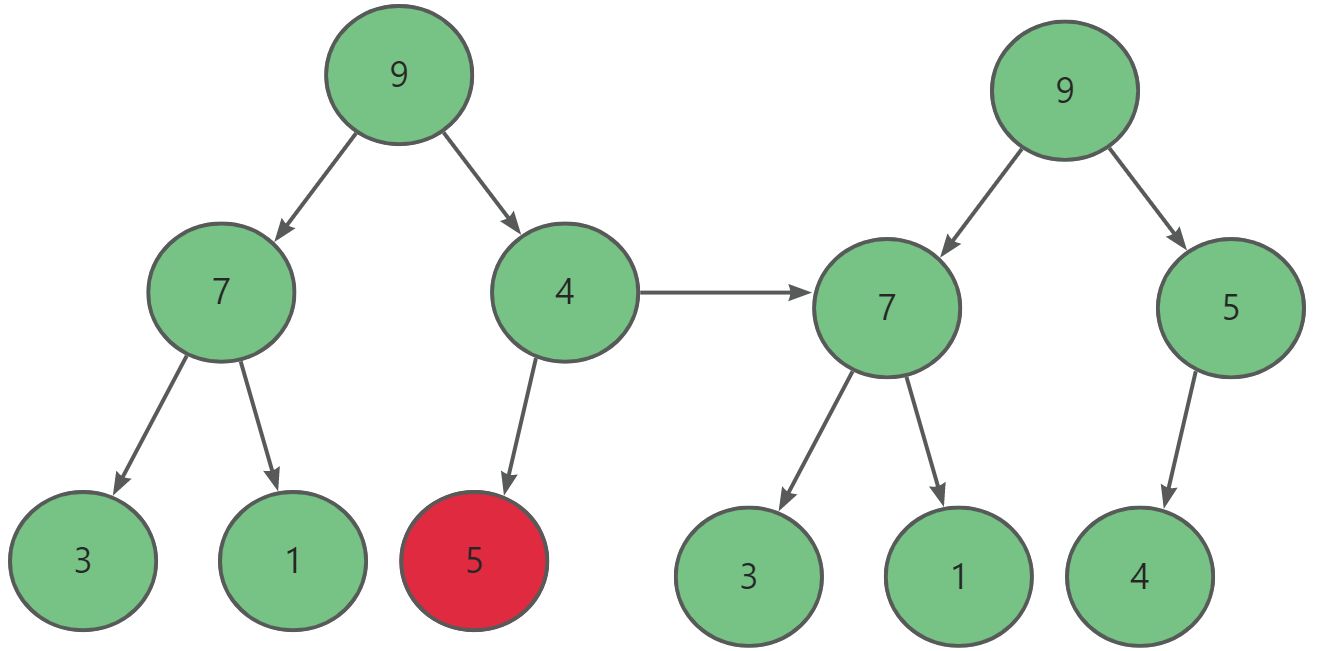
5.2.1. 代码实现

void AdjustUp(Heap* hp, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (hp->a[child] > hp->a[parent]){swap(&hp->a[child], &hp->a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPush(Heap* hp, HpDataType x)//堆的插入
{assert(hp);if (hp->size == hp->capacity){int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HpDataType* tmp = (HpDataType*)realloc(hp->a, newCapacity * sizeof(HpDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = newCapacity;}hp->a[hp->size] = x;hp->size++;AdjustUp(hp, hp->size - 1);//向上调整
}

5.2.2. 复杂度分析

时间复杂度：假设有N个节点，高度为h，2h -1=N。至少调整log2(N+1)-1次，所以时间复杂度为logN。
空间复杂度：没有开辟额外的空间，空间复杂度为O(1)。

5.3. 堆的删除

堆的删除是指删除堆顶的数据，如果我们删除堆顶元素并往前覆盖就可能打乱原有的亲缘关系。所以我们可以先将堆顶的元素与末尾元素交换，然后再进行向下调整·。

5.3.1. 代码实现

void swap(HpDataType* x1, HpDataType* x2)
{HpDataType tmp = *x1;*x1 = *x2;*x2 = tmp;
}
void 
void AdjustDown(int* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;//默认左孩子更大while (child < n){	if (child + 1 < n && a[child + 1]> a[child]){++child;//右孩子}if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(Heap* hp)//删除堆顶元素
{assert(hp);assert(hp->size > 0);swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//删除最后一个数据AdjustDown(hp->a, hp->size, 0);//向下调整
}

5.3.2. 复杂度分析

时间复杂度：假设有N个节点，高度为h，2h -1=N。至少调整log2(N+1)-1次，所以时间复杂度为logN。
空间复杂度：没有开辟额外的空间，空间复杂度为O(1)。

5.4. 获取堆顶元素

5.4.1. 代码实现

HpDataType HeapTop(Heap* hp)//获取堆顶元素
{assert(hp);assert(hp->size > 0);return hp->a[0];
}

5.4.2. 复杂度分析

时间复杂度：没有额外的时间消耗，时间复杂度为O(1)。
空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5.5. 获取堆的元素个数

5.5.1. 代码实现

size_t HeapSize(Heap* hp)//堆的大小
{assert(hp);return hp->size;
}

5.5.2. 复杂度分析

时间复杂度：没有额外的时间消耗，时间复杂度为O(1)。
空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5.6. 判断堆是否为空

5.6.1. 代码实现

bool HeapEmpty(Heap* hp)//判断堆是否为空
{assert(hp);return hp->size == 0;
}

5.6.2. 复杂度分析

时间复杂度：没有额外的时间消耗，时间复杂度为O(1)。
空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5.7. 输出堆

5.7.1. 代码实现

void HeapDisplay(Heap* hp)//堆的打印
{for (int i = 0; i < hp->size; ++i){printf("%d ", hp->a[i]);}printf("\n");
}

5.7.2. 复杂度分析

时间复杂度：遍历整个数组，时间复杂度为O(N)。
空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5.8. 建堆

5.8.1. 代码实现

void HeapCreatUp(Heap* hp,HpDataType* arr,int n)//向上调整建堆
{assert(hp && arr);for (int i = 0; i < n; i++){HeapPush(hp, arr[i]);}
}
void HeapCreatDown(Heap* hp, HpDataType* arr, int n)//向下调整建堆
{assert(hp && arr);HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}hp->a = tmp;memcpy(hp->a, arr, sizeof(HpDataType) * n);hp->size = n;hp->capacity = n;for (int i = ((n - 1) - 1) / 2; i >= 0; i--)//从最后一个元素开始{AdjustDown(hp->a, n, i);}
}

5.8.2. 复杂度分析

假设高度为h，节点个数为N。如果是向上调整建堆：

$F(N)=2^1×1+2^2×2+...+2^{h-1}×(h-1)\\ 2F(N)=2^2×1+2^3×2+...+2^{h-1}×(h-1)+2^h×(h-1)\\ 2F(N)-F(N)=-2^1-2^2-2^3-...2^{h-1}+2^h×(h-1)=-2^h+2-2^h+2^h×h\\ F(N)=2^h×(h-2)+2,N=2^h-1\\ F(N)=(N+1)×(log2(N+1)-2)+2$

如果是向下调整建堆：

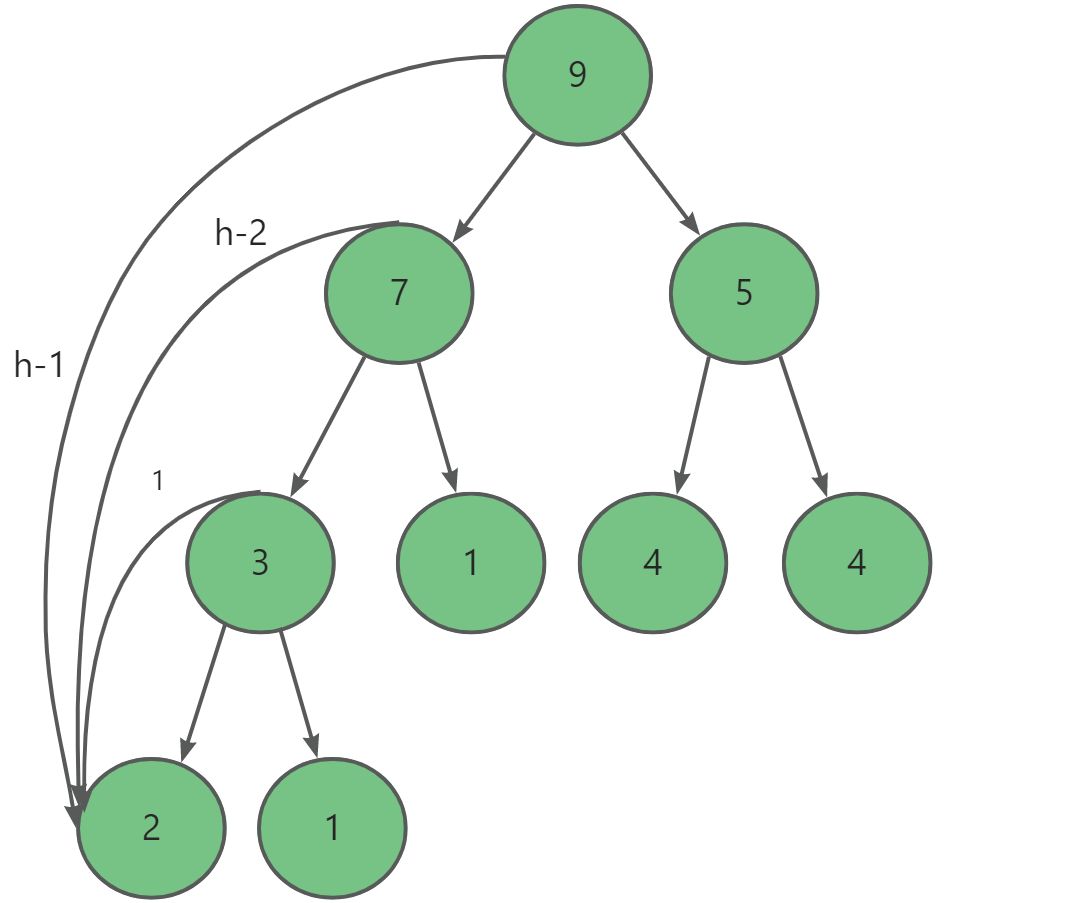
$F(N)=2^{h-2}×1+2^{h-3}×2+...+2^0×(h-1)\\ 2F(N)=2^{h-1}×1+2^{h-2}×2+...+2^1×(h-1)\\ 2F(N)-F(N)=2^{h-1}+2^{h-2}+...2^1-2^0×(h-1)=2^h-1-h\\ F(N)=2^h-1-h,N=2^h-1\\ F(N)=N-log2(N+1）$

时间复杂度：向上调整建堆最后一排调整h-1次，倒数第二排调整h-2次…时间复杂度为NlogN。向下调整建堆倒数第二排调整1次，倒数第二排调整2…第一排调整h-1次。时间复杂为O(N)。
空间复杂度：无论是向上调整建堆还是向下调整建堆都需开辟N个空间，所以空间复杂度为O(N)。

5.9. 销毁堆

5.9.1. 代码实现

void HeapDestroy(Heap* hp)//销毁堆
{assert(hp);free(hp->a);hp->size = hp->capacity = 0;
}

5.9.2. 复杂度分析

时间复杂度：没有额外的时间消耗，时间复杂度为O(1)。
空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5.10. 完整代码

5.10.1. Heap.h

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<assert.h>
typedef int HpDataType;
typedef struct Heap 
{HpDataType* a;//存储数据int size;//大小int capacity;//容量
}Heap;
void HeapInit(Heap* hp);//堆的初始化
void AdjustUp(Heap* hp, int child);//向上调整
void HeapPush(Heap* hp, HpDataType x);//堆的插入
bool HeapEmpty(Heap* hp);//判断堆是否为空
size_t HeapSize(Heap* hp);//堆的大小
void AdjustDown(int* a, int n, int parent);//向下调整
void HeapPop(Heap* hp);//删除堆顶元素
HpDataType HeapTop(Heap* hp);//获取堆顶元素
void HeapDisplay(Heap* hp);//堆的打印
void HeapDestroy(Heap* hp);//销毁堆
void HeapCreatUp(Heap* hp,HpDataType* arr, int n);//向上调整建堆
void HeapCreatDown(Heap* hp,HpDataType* arr, int n);//向下调整建堆

5.10.2. Heap.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void HeapInit(Heap* hp)//堆的初始化
{assert(hp);hp->a = NULL;hp->size = hp->capacity = 0;
}
void swap(HpDataType* x1, HpDataType* x2)
{HpDataType tmp = *x1;*x1 = *x2;*x2 = tmp;
}
void AdjustUp(Heap* hp, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (hp->a[child] > hp->a[parent]){swap(&hp->a[child], &hp->a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPush(Heap* hp, HpDataType x)//堆的插入
{assert(hp);if (hp->size == hp->capacity){int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HpDataType* tmp = (HpDataType*)realloc(hp->a, newCapacity * sizeof(HpDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = newCapacity;}hp->a[hp->size] = x;hp->size++;AdjustUp(hp, hp->size - 1);//向上调整
}
void AdjustDown(int* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;//默认左孩子更大while (child < n){	if (child + 1 < n && a[child + 1]> a[child]){++child;//右孩子}if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(Heap* hp)//删除堆顶元素
{assert(hp);assert(hp->size > 0);swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//删除最后一个数据AdjustDown(hp->a, hp->size, 0);//向下调整
}HpDataType HeapTop(Heap* hp)//获取堆顶元素
{assert(hp);assert(hp->size > 0);return hp->a[0];
}bool HeapEmpty(Heap* hp)//判断堆是否为空
{assert(hp);return hp->size == 0;
}size_t HeapSize(Heap* hp)//堆的大小
{assert(hp);return hp->size;
}void HeapDisplay(Heap* hp)//堆的打印
{for (int i = 0; i < hp->size; ++i){printf("%d ", hp->a[i]);}printf("\n");
}
void HeapCreatUp(Heap* hp,HpDataType* arr,int n)//向上调整建堆
{assert(hp && arr);for (int i = 0; i < n; i++){HeapPush(hp, arr[i]);}
}
void HeapCreatDown(Heap* hp, HpDataType* arr, int n)//向下调整建堆
{assert(hp && arr);HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}hp->a = tmp;memcpy(hp->a, arr, sizeof(HpDataType) * n);hp->size = n;hp->capacity = n;for (int i = ((n - 1) - 1) / 2; i >= 0; i--)//从最后一个元素开始{AdjustDown(hp->a, n, i);}
}
void HeapDestroy(Heap* hp)//销毁堆
{assert(hp);free(hp->a);hp->size = hp->capacity = 0;
}

6. Top-K问题

6.1. 问题分析

Top-K问题简单来说就是求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。这个问题在我们日常生活中非常常见，比如说：游戏中活跃度前十的玩家，世界五百强企业等等。

解决这个问题常见的思路就是遍历或者排序，但是当数据量较大时这种方法就并不适用了。这时我们就需要建堆来处理，具体操作方法如下：

用数据集合中前K个元素来建堆。

前k个最大的元素，则建小堆。
前k个最小的元素，则建大堆。
用剩余的N - K个元素依次与堆顶元素来比较，不满足条件则替换堆顶元素。

void TopK(int* a, int n, int k)
{//建堆int* kminHeap = (int*)malloc(sizeof(int) * k);if (kminHeap == NULL){perror("malloc fail");exit(-1);}//将前k个数据放入堆中for (int i = 0; i < k; i++){kminHeap[i] = a[i];}//向下调整法建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminHeap, k, i);}//依次比较for (int i = k; i < n; i++){if (a[i] > kminHeap[0]){kminHeap[0] = a[i];AdjustDown(kminHeap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", kminHeap[i]);}printf("\n");free(kminHeap);
}
void TestTopk()
{int n = 10000;int* a = (int*)malloc(sizeof(int) * n);srand(time(0));for (size_t i = 0; i < n; ++i){a[i] = rand() % 1000000;}a[5] = 1000000 + 1;a[1231] = 1000000 + 2;a[531] = 1000000 + 3;a[5121] = 1000000 + 4;a[115] = 1000000 + 5;a[2335] = 1000000 + 6;a[9999] = 1000000 + 7;a[76] = 1000000 + 8;a[423] = 1000000 + 9;a[3144] = 1000000 + 10;TopK(a, n, 10);
}