第二门课: 改善深层神经网络：超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)

第二周：优化算法 (Optimization algorithms)

2.3 指数加权平均数（Exponentially weighted averages）

我想向你展示几个优化算法，它们比梯度下降法快，要理解这些算法，你需要用到指数加权平均，在统计中也叫做指数加权移动平均，我们首先讲这个，然后再来讲更复杂的优化算法。

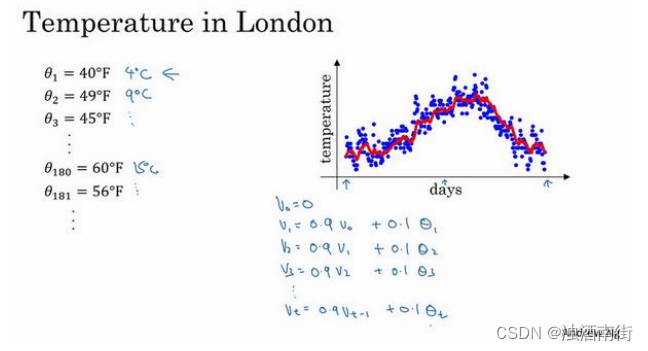
虽然现在我生活在美国，实际上我生于英国伦敦。比如我这儿有去年伦敦的每日温度，所以1 月 1 号，温度是 40 华氏度，相当于 4 摄氏度。我知道世界上大部分地区使用摄氏度，但是美国使用华氏度。在 1 月 2 号是 9 摄氏度等等。在年中的时候，一年 365 天，年中就是
说，大概 180 天的样子，也就是 5 月末，温度是 60 华氏度，也就是 15 摄氏度等等。夏季温度转暖，然后冬季降温。

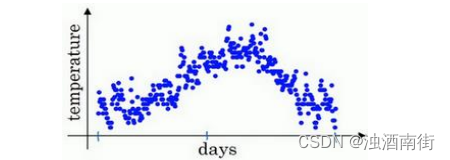
你用数据作图，可以得到以下结果，起始日在 1 月份，这里是夏季初，这里是年末，相当于 12 月末。这里是 1 月 1 号，年中接近夏季的时候，随后就是年末的数据，看起来有些杂乱，如果要计算趋势的话，也就是温度的局部平均值，或者说移动平均值。

你要做的是，首先使𝑣0 = 0，每天，需要使用 0.9 的加权数之前的数值加上当日温度的0.1 倍，即𝑣1 = 0.9𝑣0 + 0.1𝜃1，所以这里是第一天的温度值。第二天，又可以获得一个加权平均数，0.9 乘以之前的值加上当日的温度 0.1 倍，即𝑣2 =0.9𝑣1 + 0.1𝜃2，以此类推。第二天值加上第三日数据的 0.1，如此往下。大体公式就是某天的𝑣等于前一天𝑣值的 0.9加上当日温度的 0.1。

如此计算，然后用红线作图的话，便得到这样的结果。

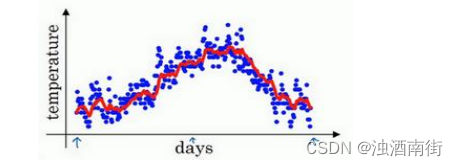
看一下上一张幻灯片里的公式，𝑣𝑡 = 0.9𝑣𝑡−1 + 0.1𝜃𝑡，我们把 0.9 这个常数变成𝛽，将之
前的 0.1 变成(1 − 𝛽)，即$$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$$

由于以后我们要考虑的原因，在计算时可视𝑣𝑡大概是 1(1−𝛽)的每日温度，如果𝛽是 0.9，你会想，这是十天的平均值，也就是红线部分。

我们来试试别的，将𝛽设置为接近 1 的一个值，比如 0.98，计算 1(1−0.98)= 50，这就是粗略平均了一下，过去 50 天的温度，这时作图可以得到绿线。

这个高值𝛽要注意几点，你得到的曲线要平坦一些，原因在于你多平均了几天的温度，所以这个曲线，波动更小，更加平坦，缺点是曲线进一步右移，因为现在平均的温度值更多，要平均更多的值，指数加权平均公式在温度变化时，适应地更缓慢一些，所以会出现一定延迟，因为当𝛽 = 0.98，相当于给前一天的值加了太多权重，只有 0.02 的权重给了当日的值，所以温度变化时，温度上下起伏，当𝛽 较大时，指数加权平均值适应地更缓慢一些。

我们可以再换一个值试一试，如果𝛽是另一个极端值，比如说 0.5，根据右边的公式（1(1−𝛽)），这是平均了两天的温度。

作图运行后得到黄线。

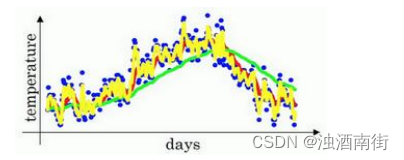
由于仅平均了两天的温度，平均的数据太少，所以得到的曲线有更多的噪声，有可能出现异常值，但是这个曲线能够更快适应温度变化。

所以指数加权平均数经常被使用，再说一次，它在统计学中被称为指数加权移动平均值，我们就简称为指数加权平均数。通过调整这个参数（𝛽），或者说后面的算法学习，你会发现这是一个很重要的参数，可以取得稍微不同的效果，往往中间有某个值效果最好，𝛽为中间值时得到的红色曲线，比起绿线和黄线更好地平均了温度。

现在你知道计算指数加权平均数的基本原理，下一个视频中，我们再聊聊它的本质作用。

2.4 理解指数加权平均数（ Understanding exponentially weighted averages）

上个视频中，我们讲到了指数加权平均数，这是几个优化算法中的关键一环，而这几个优化算法能帮助你训练神经网络。本视频中，我希望进一步探讨算法的本质作用。

回忆一下这个计算指数加权平均数的关键方程。

$$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$$

𝛽 = 0.9的时候，得到的结果是红线，如果它更接近于 1，比如 0.98，结果就是绿线，如果𝛽小一点，如果是 0.5，结果就是黄线。

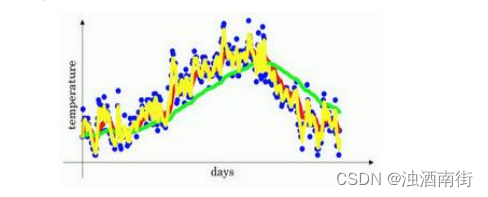
我们进一步地分析，来理解如何计算出每日温度的平均值。
同样的公式，$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$
使𝛽 = 0.9，写下相应的几个公式，所以在执行的时候，𝑡从 0 到 1 到 2 到 3，𝑡的值在不断增加，为了更好地分析，我写的时候使得𝑡的值不断减小，然后继续往下写。

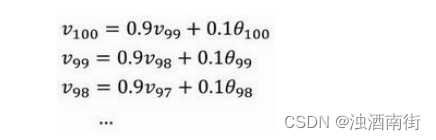
首先看第一个公式，理解𝑣100是什么？我们调换一下这两项（$0.9v_{99}0.1{\theta }_{100}$），$v_{100}=0.1{\theta }_{100}+0.9v_{99}$。
那么$v_{99}$是什么？我们就代入这个公式（$v_{99}=0.1{\theta }_{99}+0.9v_{98}$），所以：$v_{100}=0.1{\theta }_{100}+0.9(0.1{\theta }_{99}+0.9v_{98})$。
那么$v_{98}$是什么？你可以用这个公式计算（$v_{98}=0.1{\theta }_{98}+0.9v_{97}$），把公式代进去，所以：
$v_{100}=0.1{\theta }_{100}+0.9(0.1{\theta }_{99}+0.9(0.1{\theta }_{98}+0.9v_{97}))$。

以此类推，如果你把这些括号都展开，
$v_{100}=0.1{\theta }_{100}+0.1\times 0.9{\theta }_{99}+0.1\times (0.9{)}^2{\theta }_{98}+0.1\times (0.9{)}^3{\theta }_{97}+0.1\times (0.9{)}^4{\theta }_{96}+\cdots$

所以这是一个加和并平均，100 号数据，也就是当日温度。我们分析𝑣100的组成，也就是在一年第 100 天计算的数据，但是这个是总和，包括 100 号数据，99 号数据，97 号数据等等。画图的一个办法是，假设我们有一些日期的温度，所以这是数据，这是𝑡，所以 100 号数据有个数值，99 号数据有个数值，98 号数据等等，𝑡为 100，99，98 等等，这就是数日的温度数值。

然后我们构建一个指数衰减函数，从 0.1 开始，到0.1 × 0.9，到$0.1\times (0.9{)}^2$，以此类推，所以就有了这个指数衰减函数。

计算$v_{100}$是通过，把两个函数对应的元素，然后求和，用这个数值100号数据值乘以0.1，99 号数据值乘以 0.1 乘以$(0.9{)}^2$，这是第二项，以此类推，所以选取的是每日温度，将其与指数衰减函数相乘，然后求和，就得到了$v_{100}$。

结果是，稍后我们详细讲解，不过所有的这些系数（$0.1,0.1\times 0.9,0.1\times (0.9{)}^2,0.1\times (0.9{)}^3\dots$），相加起来为 1 或者逼近 1，我们称之为偏差修正，下个视频会涉及。

最后也许你会问，到底需要平均多少天的温度。实际上$(0.9{)}^{1}0$大约为 0.35，这大约是$\frac{1}{e}$，e 是自然算法的基础之一。大体上说，如果有1 − 𝜀，在这个例子中，𝜀 = 0.1，所以1 − 𝜀 =0.9，$(1-\epsilon {)}^{(\frac{1}{\epsilon })}$约等于$\frac{1}{e}$，大约是 0.34，0.35，换句话说，10 天后，曲线的高度下降到$\frac{1}{3}$，相当于在峰值的$\frac{1}{e}$。

又因此当𝛽 = 0.9的时候，我们说仿佛你在计算一个指数加权平均数，只关注了过去 10天的温度，因为 10 天后，权重下降到不到当日权重的三分之一。

相反，如果，那么 0.98 需要多少次方才能达到这么小的数值？$(0.98{)}^{5}0$大约等于$\frac{1}{e}$，所以前 50 天这个数值比$\frac{1}{e}$大，数值会快速衰减，所以本质上这是一个下降幅度很大的函数，你可以看作平均了 50 天的温度。因为在例子中，要代入等式的左边，𝜀 = 0.02，所以$\frac{1}{}$为 50，我们由此得到公式，我们平均了大约 $\frac{1}{1-\beta }$天的温度，这里𝜀代替了1 − 𝛽，也就是说根据一些常数，你能大概知道能够平均多少日的温度，不过这只是思考的大致方向，并不是正式的数学证明。

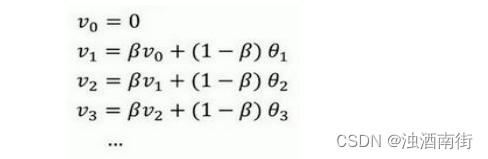
最后讲讲如何在实际中执行，还记得吗？我们一开始将$v_0$设置为 0，然后计算第一天$v_1$，然后$v_2$，以此类推。现在解释一下算法，可以将$v_0$，$v_1$，$v_2$等等写成明确的变量，不过在实际中执行的话，你要做的是，一开始将𝑣初始化为 0，然后在第一天使$v:=\beta v+(1-\beta ){\theta }_1$，然后第二天，更新𝑣值，$v:=\beta v+(1-\beta ){\theta }_2$，以此类推，有些人会把𝑣加下标，来表示𝑣是用来计算数据的指数加权平均数。

再说一次，但是换个说法，𝑣𝜃 = 0，然后每一天，拿到第𝑡天的数据，把𝑣更新为$v:=\beta v_{\theta }+(1-\beta ){\theta }_t$。指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了，正因为这个原因，其效率，它基本上只
占用一行代码，计算指数加权平均数也只占用单行数字的存储和内存，当然它并不是最好的，也不是最精准的计算平均数的方法。如果你要计算移动窗，你直接算出过去 10 天的总和，过去 50 天的总和，除以 10 和 50 就好，如此往往会得到更好的估测。但缺点是，如果保存
所有最近的温度数据，和过去 10 天的总和，必须占用更多的内存，执行更加复杂，计算成本也更加高昂。

所以在接下来的视频中，我们会计算多个变量的平均值，从计算和内存效率来说，这是一个有效的方法，所以在机器学习中会经常使用，更不用说只要一行代码，这也是一个优势。现在你学会了计算指数加权平均数，你还需要知道一个专业概念，叫做偏差修正，下一个视频我们会讲到它，接着你就可以用它构建更好的优化算法，而不是简单直接的梯度下降法。