内容概要：这篇文章浅析了张量分解（Tensor Decomposition）在数据分析和机器学习中的应用和原理。张量分解是一种在多维数据中提取特征和降维的方法，通过将高阶张量表示为低秩张量的乘积形式，实现对数据的有效表示和分解。文章介绍了张量分解的基本概念和原理，包括CP分解、Tucker分解和分解的数学表达式。并举例说明了张量分解在图像处理、信号处理和推荐系统等领域的应用场景。

适合人群：对数据分析和机器学习有一定了解，希望深入学习张量分解方法的研究人员和学习者。

能学到什么：①了解张量分解的基本概念和原理；②掌握CP分解、Tucker分解等常见的张量分解方法；③了解张量分解在不同领域的应用场景和实际案例；④理解张量分解方法的优缺点和适用范围。

阅读建议：建议学习者通过阅读本文了解张量分解的基本概念和常见方法，并结合实际案例深入理解其在数据分析和机器学习中的应用。可以进一步阅读相关文献和研究论文，探索张量分解方法的更深层次理论和应用。

Q&A

• 矩阵补全（ Matrix Completion）

  目的是为了估计矩阵中缺失的部分（不可观察的部分），可以看做是用矩阵X近似矩阵M，然后用X中的元素作为矩阵M中不可观察部分的元素的估计。

• 矩阵分解（Matrix Factorization）

  是指用 $\ast \ast U\ast V\ast \ast$ 来近似矩阵 $M$，那么 $\ast \ast U\ast V\ast \ast$的元素就可以用于估计$M$ 中对应不可见位置的元素值，而 $\ast \ast U\ast V$** 可以看做是$M$的分解，所以称作 $Matrix$ $Factorization$。

• 协同过滤【由已知信息来做预测】

  考虑大量用户的偏好信息（协同），来对某一用户的偏好做出预测（过滤）

  偏好用**评分矩阵$M$**表达后，这即等价于用$M$其他行的已知值（每一行包含一个用户对所有商品的已知评分），来估计并填充某一行的缺失值。若要对所有用户进行预测，便是填充整个矩阵，这是所谓“协同过滤本质是矩阵补全”。

• 如何进行矩阵补全

  方法：矩阵分解

  假设：如果用户A和用户B同时偏好商品 X，那么用户A和用户B对其他商品的偏好性有更大的几率相似。

  这个假设反映在矩阵M上即是矩阵的低秩。极端情况之一是若所有用户对不同商品的偏好保持一 致，那么填充完的M每行应两两相等，即秩为1。

  • 矩阵的低秩是什么意思

    矩阵的低秩是指矩阵中包含的信息量较少或者信息冗余性较高。

• 规范化因子的作用

  1. 归一化（Normalization）：通过将数据缩放到特定的范围（例如 0 到 1 或 -1 到 1），来消除不同特征之间的量纲差异。这有助于确保不同特征对模型的影响权重是一致的。
  2. 标准化（Standardization）：通过减去均值并除以标准差的方式，将数据转换为均值为 0、标准差为 1 的正态分布。这有助于使数据更符合统计假设，例如线性回归模型中的残差应该服从正态分布。
  3. 正则化（Regularization）：在机器学习中，正则化是一种用于控制模型复杂度的技术。通过添加一个规范化因子到模型的损失函数中，可以惩罚模型的复杂度，防止过拟合。

• 矩阵范数是什么

  矩阵范数是用于度量矩阵的大小或“长度”的一种数学工具。它类似于向量范数，但适用于矩阵。矩阵范数可以衡量矩阵的某些性质，如稳定性、收敛性等，并在许多领域中有着广泛的应用，包括数值分析、线性代数、控制理论、统计学和机器学习等。

  常见的矩阵范数包括：

  1. Frobenius 范数（Frobenius Norm）：也称为矩阵的欧几里得范数，是矩阵元素的平方和的平方根。对于一个矩阵 A ，其 Frobenius 范数定义为：$\Vert A{\Vert }_F=\sqrt{{\sum }_{i=1}^m{\sum }_{j=1}^n|a_{ij}{|}^2}$

     其中 m 是矩阵的行数， n 是矩阵的列数， $\ast \ast a_{ij}\ast \ast$ 是矩阵中第 i 行第 j 列的元素。

  2. 1-范数和 ∞-范数：矩阵的 1-范数是指矩阵的列向量的最大绝对值之和，而矩阵的 ∞-范数是指矩阵的行向量的最大绝对值之和。对于一个矩阵 A ，其 1-范数和 ∞-范数分别定义为：

     $$\Vert A{\Vert }_1=\underset{1\le j\le n}{\max }\sum _{i=1}^m|a_{ij}|$$

     $$\Vert A{\Vert }_{\infty }=\underset{1\le i\le m}{\max }\sum _{j=1}^n|a_{ij}|$$

     其他常见的矩阵范数还包括谱范数、核范数等。每种范数都有其特定的性质和应用场景，选择合适的范数取决于具体的问题和应用需求。

矩阵分解方法

$Basic$ $MF$（Basic Matrix Factorization）

MF视频讲解

思路：

它将用户-项目评分矩阵：$r_{3\times 3}$ 分解成两个矩阵：$u_{3\times 4}、v_{4\times 3}$，通过不断的迭代训练使得 $u\times v$ 越来越接近真实矩阵 $r$ 。

引例：

• 此处的：“小清新、重口味、优雅、伤感、五月天”，是隐含特征，给每个用户与每首音乐打上标签

实际应用：$R_{m\times n}=U_{m\times k}\times V_{k\times n}$

• 矩阵是稀疏的
• 隐含特征是不可解释的，即我们不知道具体含义了，要模型自己去学
• k 的大小决定了隐向量表达能力的强弱，k 越大，表达信息就越强，这里的理解就是把用户的兴趣和歌曲的分类划分的越具体
• 最后是通过用户矩阵 $U$ 和**物品矩阵 $V$，**预测评分矩阵

$Regularized$ $MF$

与基本的矩阵分解方法相比，Regularized MF 在优化过程中引入了正则化项，以避免过拟合和提高模型的泛化能力。

常见的正则化项包括L1正则化和L2正则化，它们分别是参数的绝对值和平方的和，用来控制参数的大小。

Regularized MF的数学推导

Regularized MF 的优化目标可以表示为：

$$\underset{U,V}{\min }:\sum _{(i,j)\in \Omega }(r_{ij}-u_i^T{v}_j{)}^2+\lambda (||U|{|}_F^2+||V|{|}_F^2)$$

其中：

• $\Omega$ 表示已知评分的索引集合；
• $\lambda$ 是正则化参数；
• $||\cdot |{|}_F$ 表示 Frobenius 范数；
• $r_{ij}$ 表示用户 $i$ 对项目 $j$ 的评分；
• $u_i$ 是用户 $i$ 的特征向量；
• $v_j$ 是项目 $j$ 的特征向量。

这个优化目标可以通过梯度下降等优化算法来求解，其中梯度的计算涉及到对损失函数的偏导数。正则化项的存在使得模型更加平滑，可以提高模型的泛化能力，防止过拟合。

Regularized MF 的迭代更新公式【具体理论：梯度下降理论】

$Regularized$ $MF$ 的目标是最小化原始矩阵 $R$ 和分解后的矩阵 $UV$ 之间的误差，同时加上正则化项以防止过拟合。根据这个目标函数，我们可以使用梯度下降等优化方法来更新矩阵 $U$ 和 $V$ 中的元素，使得目标函数达到最小值。更新公式如下：

$U_{ij}\leftarrow U_{ij}-\alpha \left(-2(R-UV{)}_{ij}{V}_{ji}+2\lambda U_{ij}\right)$

$V_{ij}\leftarrow V_{ij}-\alpha \left(-2(R-UV{)}_{ij}{U}_{ji}+2\lambda V_{ij}\right)$

其中， $\alpha$ 是学习率，控制每次更新的步长。

张量 $CP$ 分解

张量CP分解，也称为 CANDECOMP/PARAFAC（CP）分解，是一种常用的高阶张量分解方法。它将一个高阶张量表示为若干低阶张量的加权和，其中每个低阶张量是因子张量的外积。CP分解的形式可以表示为：

$\mathcal{X}={\sum }_{r=1}^R{\lambda }_r\cdot {\mathbf{a}}_r\otimes {\mathbf{b}}_r\otimes {\mathbf{c}}_r$

其中， $\mathcal{X}$ 是要分解的 $I_1\times I_2\times \cdots \times I_N$ 的高阶张量， $R$ 是分解的秩（rank）， ${\lambda }_r$ 是权重因子， ${\mathbf{a}}_r$ 、 ${\mathbf{b}}_r$ 和 ${\mathbf{c}}_r$ 分别是第一、第二和第三模态的因子向量， $\otimes$ 表示外积运算。

CP 分解可以通过多种优化算法进行求解，其中最常见的是交替最小二乘法（Alternating Least Squares, ALS）和梯度下降法（Gradient Descent）。这些算法迭代更新因子向量和权重因子，直至达到收敛条件。

CP 分解在许多领域都有广泛的应用，比如信号处理、图像处理、推荐系统、生物信息学等。它可以用于数据压缩、特征提取、异常检测等任务，同时也可以提供对数据的解释和可解释性。

张量Tucker分解

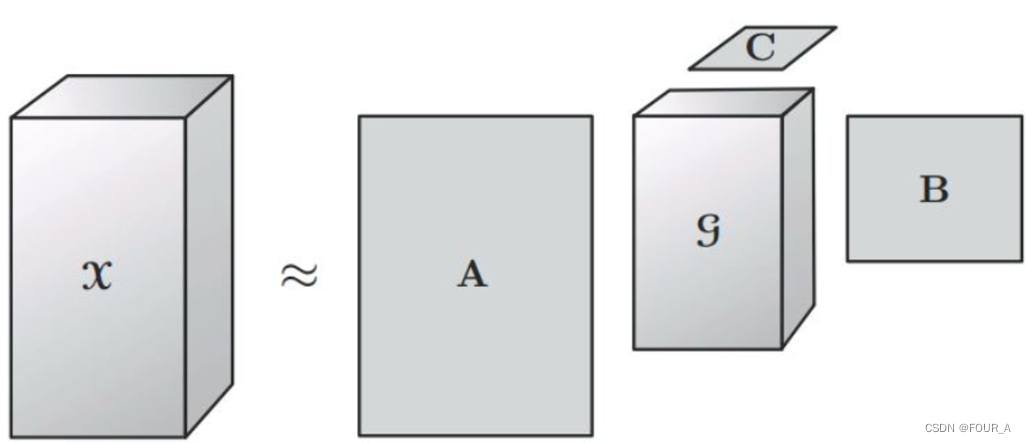
$Tucker$ 分解是一种高阶的主成分分析，它将一个张量表示成一个核心（$\mathcal{G}$）张量沿每一个 $mode$ 乘上一个矩阵。

在具体操作中，给定一个 $N-$阶张量 $\mathcal{X}$，$Tucker$ 分解将其分解为一个核心张量 $\mathcal{G}$ 和 $N$ 个因子矩阵 ${\mathbf{A}}^{(1)},{\mathbf{A}}^{(2)},\dots ,{\mathbf{A}}^{(N)}$。这种分解可以表示为：

$\mathcal{X}\approx \mathcal{G}{\times }_1{\mathbf{A}}^{(1)}{\times }_2{\mathbf{A}}^{(2)}{\times }_3\cdots {\times }_N{\mathbf{A}}^{(N)}$

其中 ${\times }_n$ 表示张量与矩阵的第 $n$ 模$（mode）$乘积。

每个因子矩阵 ${\mathbf{A}}^{(n)}$ 对应于张量 $\mathcal{X}$ 在第 n 维度上的线性变换，而核心张量 $\mathcal{G}$ 则**指定了这些因子矩阵如何相互作用来近似原始张量。**通过选择适当大小的核心张量，$Tucker$ 分解可以用于数据降维、特征提取或数据压缩。

$Tucker$ 分解在许多应用领域都非常有用，如信号处理、计算机视觉、推荐系统等。通过这种方法，研究者可以从复杂的多维数据中提取有用的信息，或者更有效地处理大规模数据集。

Tucker 分解的推导过程。

假设我们有一个三阶张量 $\mathcal{X}$ ，其维度为 $I\times J\times K$ 。我们希望将其分解为一个核张量 $\mathcal{G}$ ，以及三个因子矩阵 $U，V，W$ 。$Tucker$ 分解的目标是找到使下式最小化的 $\mathcal{G}$ 和 $U，V，W：$

$$\underset{\mathcal{G},U,V,W}{\min }\Vert \mathcal{X}-\mathcal{G}{\times }_{1}U{\times }_{2}V{\times }_{3}W{\Vert }_F^2$$

其中， ${\times }_1，{\times }_2，{\times }_3$ 分别表示在第一、第二和第三模态上的张量乘积， $\ast \ast \Vert \cdot {\Vert }_F\ast \ast$ 表示$Frobenius$ 范数。

我们可以通过交替最小二乘法来求解这个优化问题，即交替地固定 $\mathcal{G}$ ，然后更新 $U，V，W$ ，然后固定 $U，V，W$ ，然后更新 $\mathcal{G}$ 。重复这个过程直到收敛。

1. 固定 $\mathcal{G}$ ，更新 U ：
   $U=(\mathcal{G}{\times }_{1}U{\times }_{2}V{\times }_{3}W{)}^{†}\mathcal{X}$
2. 固定 U ，更新 \mathcal{G} ：
   $\mathcal{G}=\mathcal{X}{\times }_1{U}^T{\times }_2{V}^T{\times }_3{W}^T(\mathcal{X}{\times }_1{U}^T{\times }_2{V}^T{\times }_3{W}^T{)}^{†}$

其中， $(\cdot {)}^{†}$ 表示伪逆，用于求解矩阵方程中的最小二乘解。

这个过程会不断迭代，直到满足收敛条件。最终得到的 $\mathcal{G}$ 和 $U，V，W$ 就是 $Tucker$ 分解的结果。