机器学习实践——支持向量机

news/2025/1/15 20:55:45/文章来源:https://www.cnblogs.com/Linglo/p/18241979

一.什么是支持向量机

支持向量机（SVM）是一种广泛使用的监督学习方法，主要用于分类和回归分析。它的基本原理是找到一个超平面（在二维空间中是一条直线），以最大化不同类别之间的边界。以下是SVM的关键概念：

超平面：决策边界，用于分类的直线或平面。
边界（Margin）：从超平面到最近的数据点的最小距离。SVM的目标是最大化这个边界，以提高模型的泛化能力。
支持向量：距离超平面最近的那些数据点，它们直接影响超平面的位置和方向。
核技巧：通过将数据映射到更高维的空间来处理非线性可分的情况，使得在新的空间中数据可线性分割。

SVM在处理高维数据和解决非线性问题方面表现出色，尤其是在样本数量较少的情况下。它们在图像识别、生物信息学和其他许多领域都有应用。

二.SVM原理

2.1边界和支持向量

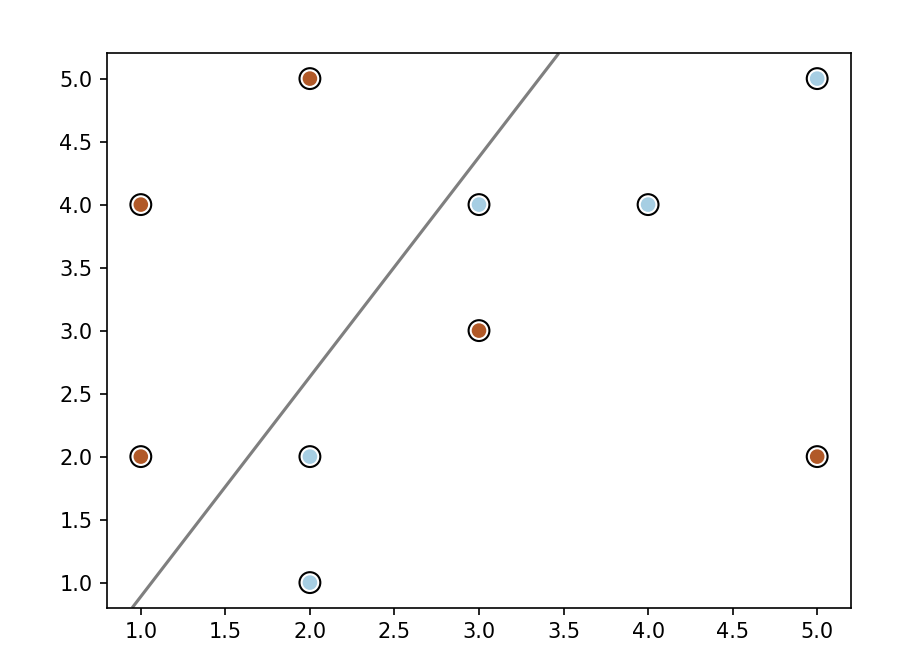
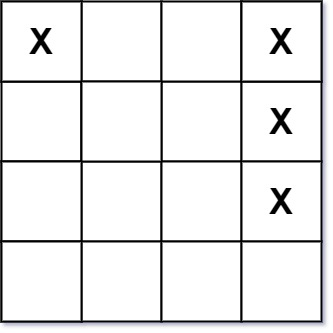
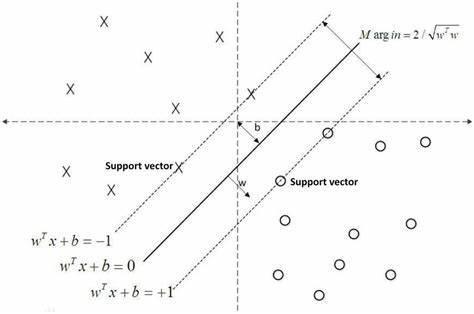
想象一个二维平面，平面上有两类数据点，一类用圆圈表示，另一类用叉号表示。这些点分布在平面的不同区域，但彼此接近。

在这些点中间，有一条直线，这就是决策边界或超平面。这条直线的两侧各有一条虚线，这两条虚线与决策边界平行，并且与最近的数据点有相同的距离。这段距离就是边界（Margin）。

在每条虚线上，至少有一个圆圈或叉号的数据点，这些点就是支持向量。支持向量是最靠近决策边界的点，它们直接影响边界的位置。

这个二维的示意图清晰地展示了SVM的工作原理：通过最大化边界来找到最佳的决策边界，从而有效地区分两类数据点。

2.2确定超平面

确定支持向量机（SVM）中的超平面是一个优化问题，其目标是找到一个能够最大化不同类别之间边界（Margin）的决策边界。以下是确定超平面的步骤：

1. 定义目标函数：SVM的目标是最大化边界。可以通过最小化以下目标函数来实现：
$$
\text{Minimize } \frac{1}{2} \|w\|^2
$$
其中，$w$ 是超平面的法向量。

2. 添加约束条件：为了确保所有数据点都正确分类，添加以下约束条件：
$$
y_i (w \cdot x_i + b) \geq 1 \quad \text{for all } i
$$
其中，$y_i$ 是第 $i$ 个数据点的标签（+1 或 -1），$x_i$ 是第 $i$ 个数据点，$b$ 是偏置项。

3. 构建拉格朗日函数：结合目标函数和约束条件，构建拉格朗日函数：
$$
L(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^{n} \alpha_i [y_i (w \cdot x_i + b) - 1]
$$
其中，$\alpha_i$ 是拉格朗日乘数。

4. 求解对偶问题：通过对 $L(w, b, \alpha)$ 求偏导数并设置其为零，得到对偶问题。求解对偶问题得到 $w$ 和 $b$ 的最优值：
$$
\text{Maximize } \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j)
$$
$$
\text{Subject to } \sum_{i=1}^{n} \alpha_i y_i = 0 \quad \text{and} \quad \alpha_i \geq 0 \text{ for all } i
$$

5. 确定支持向量：非零的 $\alpha_i$ 对应的数据点即为支持向量。

通过这些步骤，可以确定最优的超平面，用于分类任务。

2.3核函数

在支持向量机（SVM）中，核函数是用来将非线性可分的数据映射到一个高维空间，使其在这个新空间中线性可分。这是一种处理非线性问题的技巧，它允许SVM在原始空间中找到复杂的边界。核函数的选择取决于数据的分布和问题的性质。

常见的核函数包括：

1. 线性核（Linear Kernel）
- 用于线性可分数据。
- 计算两个向量的内积。

2. 多项式核（Polynomial Kernel）
- 可以学习数据的更高维特征表示。
- 参数包括多项式的阶数。

3. 径向基函数核（Radial Basis Function Kernel，或高斯核 Gaussian Kernel）
- 非常强大，可以映射到无限维空间。
- 常用于处理不同类型的非线性问题。

4. Sigmoid核
- 类似于神经网络中的sigmoid激活函数。
- 可以用于模拟两层神经网络。

核函数的选择

选择核函数时，通常需要考虑以下因素：

- 数据的特性：线性可分数据使用线性核，非线性数据根据分布选择其他核。
- 问题的复杂性：简单问题使用简单核，复杂问题可能需要复杂核。
- 计算资源：有些核函数（如RBF）可能会导致计算量大增。
- 过拟合风险：复杂的核函数可能会导致模型过拟合。

核函数的数学表达

以高斯核为例，其数学表达式为：

$$ K(x, x') = \exp\left(-\frac{||x - x'||^2}{2\sigma^2}\right) $$

其中，$x$ 和 $x'$ 是两个输入向量，$\sigma$ 是高斯核的宽度参数。

三.SVM代码实现

3.1简单线性可分SVM实现代码

线性可分

import matplotlib.pyplot as plt
import numpy as np
训练数据和标签
X = np.array([[2, 2], [4, 4], [1, 4], [3, 3]])  # 特征集

y = np.array([-1, -1, 1, 1])  # 标签集
初始化权重和偏置
w = np.zeros(2)

b = 0
学习率和迭代次数
learning_rate = 0.01

epochs = 1000
训练过程
for epoch in range(epochs):

for i, x in enumerate(X):

if y[i] * (np.dot(w, x) + b) < 1:

w += learning_rate * (y[i] * x - 2 * w)

b += learning_rate * y[i]

else:

w -= learning_rate * 2 * w
绘图函数
def plot_svc_decision_boundary(w, b, X, y):

# 绘制数据点

plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
# 创建网格以绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()# 创建网格来评估模型
xx = np.linspace(xlim[0], xlim[1])
yy = np.linspace(ylim[0], ylim[1])
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = np.dot(xy, w) + b# 决策边界和边界
Z = Z.reshape(XX.shape)
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])# 支持向量
ax.scatter(X[:, 0], X[:, 1], s=100, linewidth=1, facecolors='none', edgecolors='k')
plt.show()

绘制数据点和决策边界
plot_svc_decision_boundary(w, b, X, y)